地震作用下骆驼城土遗址的安全性评价①

石玉成，李 舒，刘 琨

（1.中国地震局兰州地震研究所，甘肃 兰州 730000；2.中国地震局黄土地震工程开放实验室，甘肃 兰州 730000；3.甘肃省岩土防灾工程技术研究中心，甘肃 兰州 730000；4.东南大学土木工程学院，江苏 南京 210008）

0 引言

土遗址指的是主要建筑材料以土为主的古遗址，是一种宝贵的不可移动文物。由于特殊的环境条件，在我国西北地区有有大量的土遗址赋存，主要有古城、长城、关隘、烽燧、土塔及陵墓等。土遗址主要建造工艺有夯筑、直接利用生土挖造、土坯砌筑、板筑泥建造。近年来，对于土遗址的保护研究工作一直开展得如火如荼，其中主要成果包括文献［1－4］等。大部分研究集中在对土遗址的防风化、化学加固方面。对于土遗址的抗震安全性评价方面，文献［5、6］做了土遗址动力稳定性研究，文献［7］对未来地震对于不可移动文物遗址的影响进行了研究。由于土遗址的种类和形式极其繁多，很难以一个确定性的模型或计算方式来获取较为准确的结论，即便是赋存于同一地点，也会因各具其特征，造成结论普遍适用性缺乏。本文以甘肃高台县境内国家级重点保护文物单位骆驼城土遗址为例，对其进行抗震性能分析并寻求一种新的土遗址抗震安全性评价方法。

1 骆驼城土遗址简介

骆驼城位于甘肃高台县城西20km处。始建于东晋陲安元年，即公元397年。是后凉建康郡太守段业另立年号建立的北凉国国都。骆驼城面积299200m2，是目前国内现存最大、保存最为完整的汉唐古城土遗址，是国务院公布的第四批全国重点文物保护单位。然而在经历了一千多年的风吹日晒、水流侵蚀、地质应力、生物虫害、人为破坏等因素，骆驼城土遗址出现了基础蚀空、大片裂隙、部分坍塌、局部失稳或构筑材料的力学性能发生明显下降等病害。如图1所示。当发生地震时，区域烈度达到Ⅶ度甚至不及Ⅶ度时，骆驼城城墙极有可能发生全部或部分倒塌（坍塌），或结构失稳等不可修复之破坏。

图1 骆驼城土遗址病害Fig.1 Diseases of the Camels town soil relics.

2 土遗址结构抗震可靠度基本理论和概率性分析方法

2.1 抗震可靠度定义

根据工程结构可靠度设计规范给出的可靠度定义，结合土遗址结构抗震分析本身，土遗址结构抗震可靠度可定义为：土遗址结构在未来不同烈度的地震作用下，不发生失稳破坏的概率，即为判断土遗址结构抗震安全性的概率量度。

土遗址结构的抗震稳定性功能可表达为［9］

式中：Z为一随机变量；R为土遗址的地震抗力；S为地震荷载效应。R、S均为多个基本随机变量x1，x2，…，xn的函数，则结构功能函数的一般形式为Z＝g（x1，x2，…，xn）。结构的失效概率为

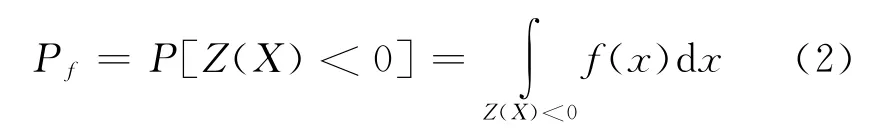
其中f（x）为随机变量的联合概率密度函数。

2.2 抗震概率性分析的适用性讨论

2.2.1 概率性分析适用于土遗址抗震分析的主因

对于大型岩土体结构－土遗址结构而言，存在许多不定性影响因素。引入可靠度理论进行概率性抗震分析，是一种较为科学、全面的抗震安全性评估新方法。以骆驼城土遗址为例，采用抗震概率性分析的主要适用性体现如下：

（1）土遗址几何参数的不定性

同其它大型土遗址结构一样，骆驼城城墙是分段夯筑，中间存在着结构缝隙，这是为了夯筑方便，同时也是为了应对温度变化引起的墙体收缩或膨胀。那么对城墙进行抗震分析时必须选取两条结构缝间的一段相对独立墙体进行模拟计算，而每条结构缝的间距（墙体相对独立长度）由于初期修建或后期产生的新裂缝而不尽相同。如何确定每段墙体的长度成为首要的问题，如果使用一个确定性的数值，譬如10m，则此模型就不具有整片区域内骆驼城城墙的代表性，与此同时，也无法得知由于墙体相对独立长度的变化导致的结果变异程度。

（2）土遗址材料性能的不定性

土遗址在砌筑时均取材当地，即利用当地的黄土、生土进行夯筑而成。由于建造年代（维修年代）的不同，取材地点的不同，在历经千百年的风雨后，其建造材料的物理力学性质会由于地点的不同而存在着较大的差异。即使是位处一地的土遗址，也会由于地势的起伏，受水浸泡的程度不同；或是由于顺风面和逆风面的土遗址会受到不同程度的风化侵蚀，从而造成材料性质上的差别。图2所示为驼城土遗址的不同方位的城墙因地势高低和城墙走向的不同，导致受风化和侵蚀的程度存在较大差异。就土遗址的抗震稳定性分析而言，材料参数包括：土遗址材料密度、弹性模量、压缩模量、泊松比、粘聚力、内摩擦角、抗剪强度等，这些参数会在一定范围内变化，具有一定的客观不确定性。

图2 骆驼城南北城墙风化程度对比Fig.2 Comparison of weathering degree between north and south walls of Camel town.

（3）地震作用的不定性

由于震源机制、震源深度、震级等方面因素的差异导致地面运动的差异，最直观的表现应该为最大地震加速度即PGA的差异。在不同地震过程中对应的PGA值是不同的，其离散性比较大。符合实际的做法则是将加速度峰值作为随机变量，在大量收集有关地震资料后进行统计分析，确定加速度峰值的概率分布函数。

（4）土遗址结构地震抗力的不定性

对土遗址结构进行数值模拟，进行抗震稳定性分析，首先必须通过实验室实验对土遗址的构筑材料进行物性指数分析。通常以本构关系曲线中提取的材料极限应力或极限应变值作为结构的破坏阈值。在实验过程中通常会选取几组样品，其实验结果会产生一定的离散性。此外，由于土遗址建造方式的不同以及实验条件或方法的局限性，也会导致土遗址整个结构在地震作用下破坏时的极限应力、应变值与实验室的实验数值存在一定偏差。

2.2.2 概率性分析适用于土遗址抗震分析的优势

因此，综合以上四方面不定性的因素，我们可以通过现场勘查测绘，室内土工实验，规范给出的统计参数，以及参数估计等手段计算得到各因素的分布类型及分布参数，以消除其不确定性。然后基于可靠度理论进行抗震概率分析，一方面可以得出土遗址结构模型在地震作用下最大单元位移、应力、应变和失效概率等常规性结论，另一方面可以分析这些计算结果对于土遗址的几何尺寸或材料参数在抗震分析中所占的敏感度大小，即参与计算的每一方面因素在土遗址结构的抗震稳定分析中所占的重要性比例都会有明确表达。此外可以得出不同参变量之间的相关性（不同事物部分或在某种程度上受同一原因支配的特性），譬如土遗址的重力和地震力、抗力与最大应力、材料的凝聚力和内摩擦角的相关性等。以上三方面的重要意义在于不仅在于将土遗址结构的抗震安全性评价与土遗址的内在本质结合起来，更重要的是可以通过分析结果，确定土遗址在后期加固防护工作的方向与重点。

2.3 结构抗震概率性分析方法

目前常用的可靠度分析方法，如一次二阶矩法、帕尔黑莫法及JC法等，只有当极限状态方程为线性、各随机变量服从正态分布时，得到的可靠指标才是精确的，否则必须采用线性化或当量正态方法进行处理。而Monte－Carlo法不受上述条件限制。只要模拟次数足够多，就可得到相对精确的失效概率值，且还可以方便地求解体系可靠度。为此，本文采用Monte－Carlo法，结合有限元软件计算效率高、不受模型限制的优点，编制APDL程序，来研究骆驼城土遗址的抗震稳定性问题。其计算流程如图3所示。

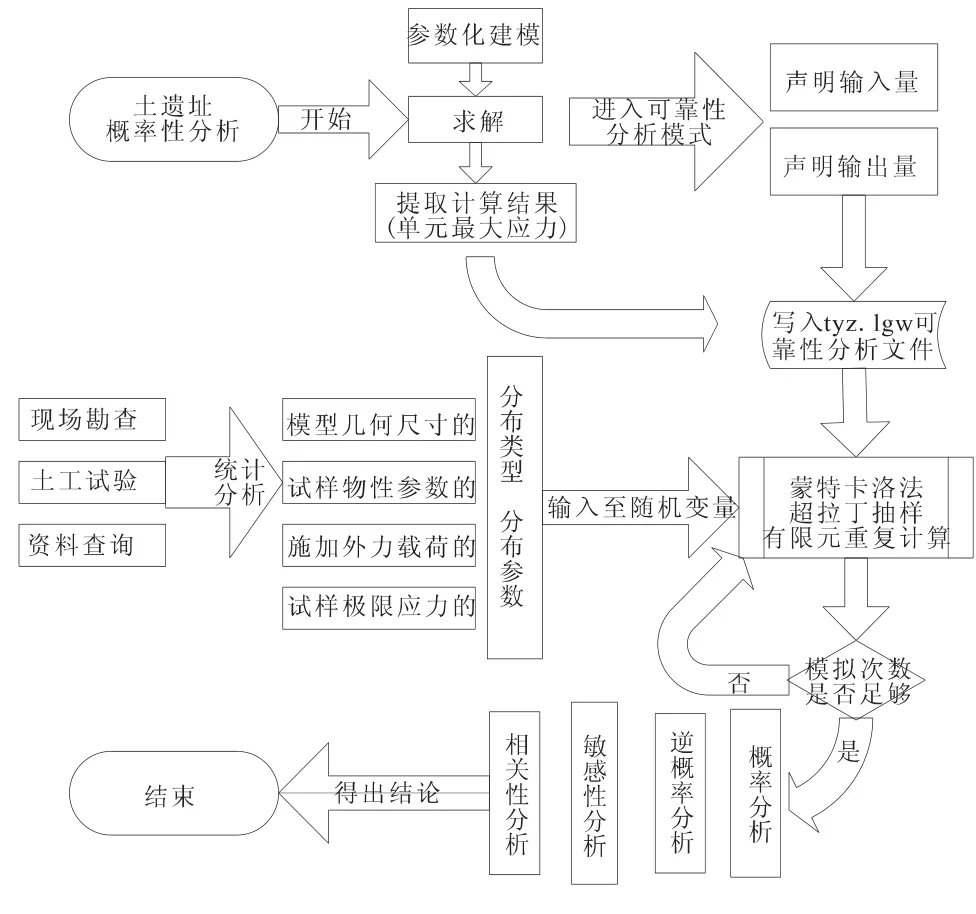
图3 土遗址可靠度分析流程图Fig.3 Flow chart of reliability analyzing to soil relics.

3 骆驼城城墙计算实例

3.1 样品采集

本着保护文物的原则，从散落在周边的城墙土中取出所需部分，带回实验室进行室内土工试验。主要实验内容包括获取弹性模量、密度、泊松比、静强度、含水量等数据。

3.2 计算所需各随机变量的分布类型及分布参数

根据对实验和原位动力测试数据的整理分析，利用MATLAB进行数据统计，计算出均值及方差，如表1所示。

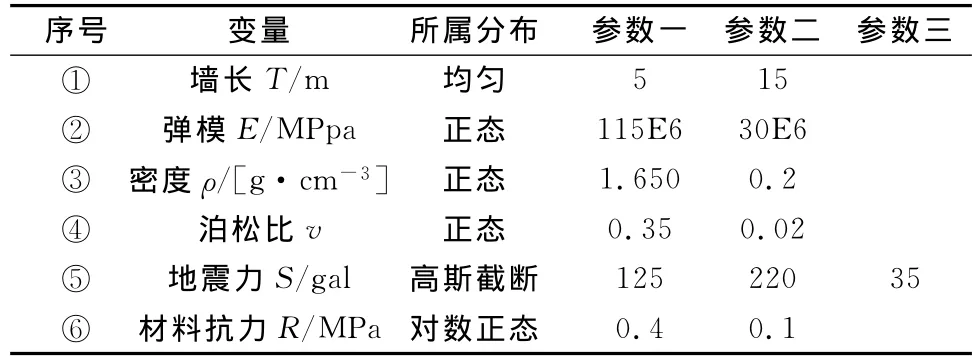
表1 随机变量的统计参数

表中各参数取值说明如下：

（1）序号①中参数一、二分别表示墙体相对独立长度的下界和上界；序号⑤中参数一、二、三分别表示均值、截断上界、截断下界；其余序号中参数一、二均分别表示均值与方差。

（2）在现场对各相对独立段城墙的长度进行抽样测量，发现基本居于5～15m之间，数据较平均。有些是天然留下的夯筑缝，有些则是在后期形成并发展的大裂缝，以至于墙体被隔断。因此长度T取均匀分布较为合适。

（3）弹性模量：根据城墙土体波速测试结果和理论公式以及实验室土工实验（静弹性模量）的数据，利用MATLAB统计，计算出期望与方差。

（4）密度：根据实验室土工试验结果，结合《结构可靠度设计标准》规定，当材料物性参数样本缺乏或不足时，可认为材料参数服从正态分布。采取人工扩充样本的方法，利用MATLAB统计，计算出期望与方差。

（5）泊松比：同（4）。

（6）地震力（研究区）：地震烈度与地面峰值加速度的关系采用下式：A＝10（Ilg2－0.01），计算得到截断高斯分布的期望值为1.25m／s2；Ⅶ度抗震设防区域的超越63.5%概率的人工加速度峰值为0.35 m／s2，作为截断的下限；据《建筑抗震设计规范GB50011－2001》规定，抗震分析时，Ⅶ度区域的加速度峰值不超过2.20m／s2，作为截断的上限。

（7）阈值：即实验中土体试样的等效极限应力。据《结构可靠度设计规范》规定，因为土体的极限应力与以上所述的（3）－（6）均有关，与它们存在着卷积的关系。因此阈值应服从对数正态分布。具体分布参数可通过人工扩充样本后，利用MATLAB进行统计得出结果。

3.3 参数化建模

3.3.1 初期试算

利用APDL语言编程，进行参数化建模，在ANSYS中进行抗震试算并调整。提取单元（节点）的最大主应力、等效应力等重要结果。

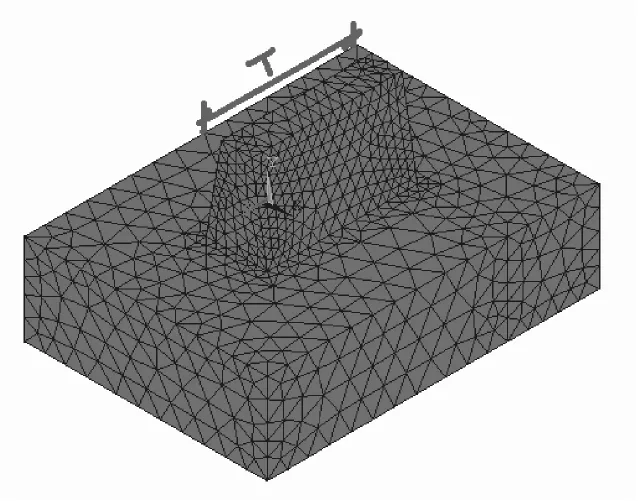
图4 城墙有限元模型Fig.4 FEM model of city wall.

骆驼城城墙是直接建造在土体之上的夯土建筑物，模型尺寸为顶端2.0m，底部宽4.0m并沿梯度方向延伸2m，墙顶至地面高度6.0m，长度为变量T。底部与大地相连接，取地下深度4.0m，宽为10 m的实体作为基座，长度也为T，城墙主体材料参数采用服从某种分布的随机变量。由于关注的主体非基座，因此基座采用确定性的参数输入，具体参数参照文献［10］中的土坯土工实验的结果，如表2所示。

表2 基座材料参数

边界条件的处理：边界的约束条件取刚性约束。本文中为了减少约束的个数，对模型上部采用自由边界条件处理，具体的施加办法如下：

上部边界：自由；基座两侧边界：与X轴同向取UX＝0；与Y轴同向取UY＝0；基座底面：UX＝UY＝UZ＝0。

为提高计算效率，城墙主体与基座部分采用不同精度的划分，城墙部分采用高精度全自动适应网格划分，基座部分采用较低精度划分（图4）。

在地震动输入过程中，采用一致激励法，即对垂直于城墙走向方向输入可变惯性加速度S，进行动力计算，并将结果按降序排列。发现位于墙顶靠近端部的173号单元的应力值为最大，因此，提取173号单元计算结果，并声明为输出变量，作为概率性分析的前提准备，藉此与土遗址抗震安全阈值（材料的最大的等效应力）做比较，得出结论。

3.3.2 基于可靠度理论的抗震概率性分析

图5是弹性模量E和地震力S的分布图。

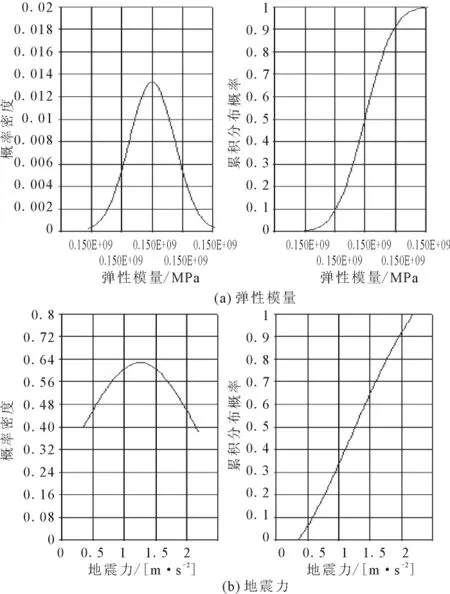
图5 输入变量参数分布Fig.5 Parameters distribution of input variable values.

图6显示的是第173号单元的最大应力在每次循环中的结果实时显示。从图中所示可以看出，绝大部分随机计算结果，应力大小在0.1MPa与0.4 MPa之间。

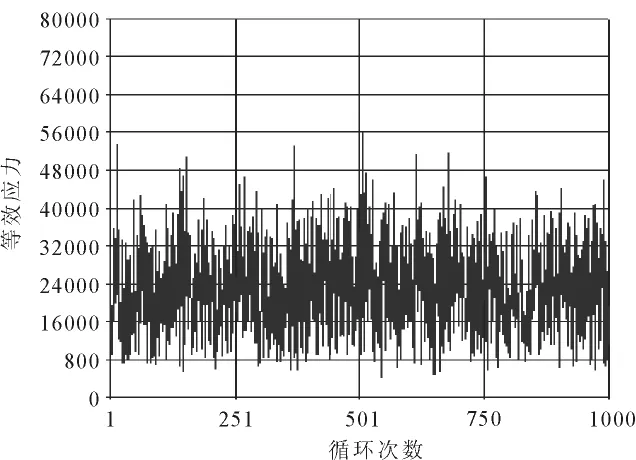
图6 最大应力随循环次数时程Fig.6 Maximum stress along with cycling history.

图7所示的是模型单元的应力均值随模拟次数的变化规律。由图可见，均值随着模拟次数的增加渐趋于一个平稳值，表明模拟次数已足够。

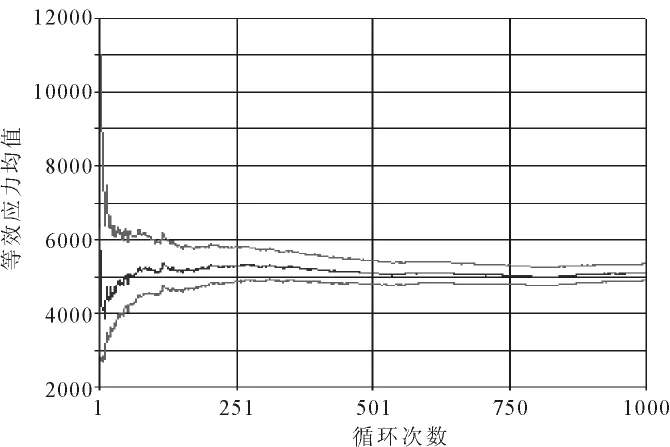
图7 均值随循环次数变化规律Fig.7 Regularity for mean value change with cycling.

图8所示的是第173号单元应力作为随机输出变量的分布函数图。从图中可以看出，在地震力作用下，单元应力大于0.051MPa或小于0.5MPa的概率为100%。当随机变量Z＜0，即表示在地震力作用下土遗址结构的失效概率。在软件中输入材料极限强度值及分布类型和参数，即可显示失效概率为7.2%。反之，也可进行逆概率计算，即证明如若在抗震设防烈度为Ⅶ度、结构破坏概率不超过1%的条件下，单元的最大等效应力不得超过0.487 MPa。以上的计算结果均是在95%的置信度下统计得到的。

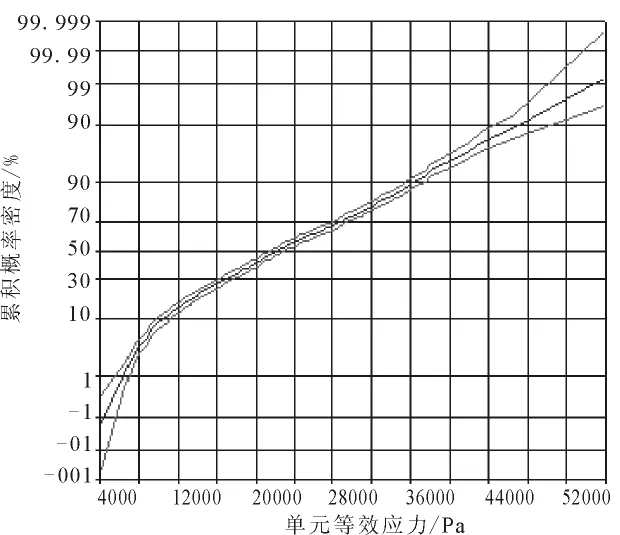
图8 单元等效应力分布函数Fig.8 Cumulative distribution function of element stress

3.3.3 计算结果对于输入变量的敏感性

根据对随机输入变量的相关性分析，可以得出在土遗址的地震响应分析中各参量对其影响的权重比例及影响方式，如图9所示。

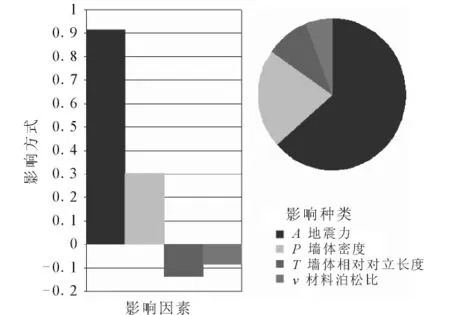
图9 输出变量对输入变量的敏感度Fig.9 Sensitivities of output variable to input variable.

由图9知：骆驼城土遗址在地震中发生结构失效的主导因素按重要性排列分别为：地震力大小、墙体密度、墙体的相对独立长度和材料泊松比。其中地震力的大小在计算中占主导作用，地震力和墙体密度与计算结果呈正相关关系，即节点的最大应力或结构的失效概率随着地震惯性力的增大而增加；材料的泊松比和墙体的相对独立长度与计算结果呈负相关关系，即随着材料泊松比数值的增大，结构的失效概率降低；而模型的长度T也占据了很重要的部分因素，城墙的相对独立长度越大，稳定性越好。因为进行的是伪动力计算，所以阻尼比因素不予考虑，弹性模量在此计算过程中对结果产生变异性的效果不明显。

通过敏感度的计算，为我们提供了参考性的建议。譬如，在骆驼城城墙遗址的抗震保护及加固的过程中，应该加强土遗址中局部应力集中的部位，以抵抗较大烈度的地震。同时，可以通过物理或化学加固方法，填补城墙间的缝隙或改善风化严重的墙面状况，增加各段城墙间的联结性，藉此来改善土遗址的抗震性能等。

4 结语

本文通过室内土工实验、运用统计学相关知识、以及集合有限元软件建立模型方便、计算高效准确的特点以及可靠度相关理论在土遗址抗震中的较强适用特性，对骆驼城土遗址在未来50年内地震作用下的稳定性做了概率性分析。此种手段可作为一种评价土遗址抗震安全性的新方法，效果直观明显。通过计算研究，可以获得如下结论：

（1）在未来50年内，当研究区域发生地震时，土遗址结构的稳定概率达到92.8%以上，或土遗址结构的失效概率小于7.2%。

（2）在未来50年内，当研究区域发生地震时，若要保证99%结构稳定概率的前提条件下，土体中产生的最大等效应力不得超过0.487MPa。

（3）地震力大小在土遗址抗震稳定性能占主导作用，而各相对独立城墙段的不同长度、墙体密度、材料泊松比等其余物性参数亦会对抗震性能产生不同程度的影响，这为后续的土遗址抗震加固工作提供依据参考。在对土遗址抗震稳定问题的未来研究中，可通过可靠度分析来研究其失效规模及失效模式等，更进一步地对土遗址的防灾减灾问题进行深入研究。

［1］李最雄.丝绸之路古遗址保护［M］.北京：科学出版社，2003.

［2］李最雄，王旭东.古代土建筑遗址保护加固研究的新进展［J］.敦煌研究，1997，（4）：167－172.

［3］石玉成，蔡红卫，徐晖平，等.石窟围岩及其附属构筑物地震稳定性评价方法研究［J］.西北地震学报，2000，22（1）：83－89.

［4］Robert E Englekirk.Geotechnical Issues in the conservation of sites.Conservation of Ancient Sites on the Silk Road［A］∥Neville Agnem，edite.Proceedings of an International Conference on the Conservation of Grotto sites［C］.［s.l.］：Getty Publications，1997：147－158.

［5］刘琨，石玉成，卢玉霞，等.玉门关段汉长城墙体结构抗震性能研究［J］.世界地震工程，2010，26（1）：47－52.

［6］石玉成，胡明清，李舒.不同地震荷载作用下土遗址的动力响应分析［A］∥岩石力学与工程的创新和实践：第十一次全国岩石力学与工程学术大会论文集［C］.湖北：科学技术出版社，2010：98－103.

［7］石玉成.未来地震灾害对敦煌莫高窟及其附属建筑物的影响［J］.西北地震学报，1996，18（3）：42－47.

［8］Zhang Shi－zheng.The elementary method of architectural reliability and realization by software named ANSYS［J］.Journal of Guangxi University （Natural Science Edition），2006，31（21）：34－37.

［9］王峻.黄土地区农村民房生土建筑墙体材料抗震性能试验研究［J］.西北地震学报2005，27（2）：158－162.