岩石滞后非线性弹性响应的物理模型①

任 隽，陈东柏，戴王强，陈运平，潘纪顺

（1.长安大学，陕西 西安 710064；2.陕西省地震局，陕西 西安 710068；3.中南大学地学与环境工程学院计算地球科学研究中心，湖南 长沙 410083；4.华北水利水电学院资源与环境学院，河南 郑州 450011）

0 引言

地壳岩石的非线性响应是一个十分丰富的话题，可广泛应用于地震工程、无损检测和材料科学。地壳岩石实际上是一种高度多组分、非均匀的材料，它的宏观弹性特性比组成它的材料要复杂得多。组成岩石的矿物颗粒本身是非常坚硬的，岩石中还包含颗粒间的接触、微裂纹、孔洞等，它们之间由粘结介质等联接在一起形成弹性体。颗粒的刚度较大，受到载荷作用时变形较小；粘结介质的刚度较小，受到载荷作用时变形较大；裂纹受到载荷作用时会滑动、闭合或者扩展。这样岩石由硬软两部分组成：坚硬部分为岩石颗粒，软弱部分为胶结物、位错、微裂纹和孔洞等粘结系统。岩石颗粒在体积上比粘结系统要大得多，它们的力学性质也相差很大，岩石强烈的非线性是与其硬软两部分的存在相关的。粘结系统只占了岩石相当小的体积，但是受到载荷作用时变形较大，对岩石的力学性质的影响最大，几乎可以说是它们决定了岩石的力学性质［1］。岩石内部结构复杂，受到载荷作用时，表现出的不是线弹性，而是非线性，由于岩石特殊的细观结构，这种非线性不同于一般的非线性弹性材料，包括滞后［2－9］和弛豫（慢动力）［10－12］。对于周期性荷载的岩石来说，其表现出来的非线性弹性关系体现在应变与应力之间的相位滞后［6－7］。现在也逐渐清楚，粘结系统中的流体对非线性响应的贡献特别显著，但是，粘结系统和和孔隙流体究竟是如何影响非线性响应的，目前还没有搞清楚。

导致这些不寻常行为的物理机制到目前还没有揭开。岩石是固结材料，因而石英晶体的弹性响应与石英砂岩的弹性响应之间几乎没有什么关联。岩石的弹性性质主要是颗粒间的粘结自然属性的结果，而不是这些颗粒本身。岩石内部的粘结系统对温度、孔隙流体的属性和应力是十分敏感的。因此，正是岩石的粘结系统的响应使其具有非线性和滞后性。

岩石适当的物理模型必须与它们复杂的结构相联系。本文将介绍几个简单的物理模型，以探讨岩石非线性响应的微观机理。

在传统的弹性理论中，介质非线性的理论模型是基于应变能方程的展开或者保留低阶（二阶和三阶）非线性项的应力－应变状态方程。对于传统的能量展开，应力－应变关系可以写成

其中M是弹性模量；β和δ是非线性系数。但是对于具有滞后和弛豫特性的地球材料来说，本构关系式可能会显得复杂而多样。经常见到的例子是振幅相关的摩擦：当介质受到相当大的震荡作用时，可观察到异常高的能量损失；杨氏模量会随着应变振幅的变化而变化。在某种程度上，这样的材料显示了滞后行为，这种滞后行为与机械缺陷的不可回复运动（也就是微塑性变形）有关。振幅相关的摩擦效应在很大的频率（1～106Hz）、温度（300～3 800K）、和变形振幅（ε～10－6～10－2）范围内受到关注。为了解释这些事实，必须寻找岩石静态和动态行为的更普遍的模型。

1 颗粒接触模型

最早用来解释岩石非线性的模型是赫兹颗粒接触模型，它是把岩石作为干燥的接触颗粒的系统看待的（图1）。这些接触比基质材料－颗粒本身要软得多，因此在介质的非线性弹性响应中起到主要的作用。在这个模型中，两个半径为R的颗粒发生了接触，在受到正压力F的作用下，两个颗粒在接触点上发生了弹性变形。分离距离（即颗粒中心连线之间的距离）的改变量Δ为［13］

式中：E为材料的杨氏模量；ν为泊松比；R是颗粒半径。

图1 赫兹接触模型示意图Fig.1 Sketch of the Hertz contact model.

岩石力学实验中，岩石受到静态压力引起一个固定的预应变ε0。在地壳岩石中，预应力可能来自地球上层的压力，也可能来自岩石材料接触点处坚硬的固结部分，或者两者兼而有之。对于小的一维扰动，二次和三次非线性系数为

非线性参数（式3）不依赖于颗粒尺寸或它们的成分，而是依赖于预应变ε0，也就是依赖于静态压力，这意味着超压越大，材料的非线性越小。

上世纪六七十年代就开始研究岩石中地震波的非线性衰减现象了，这涉及到了岩石滞后的物理微观机制问题。经典的解释是颗粒接触面和颗粒边界之间的滞后摩擦滑动［14－16］。1971年Johnson等人在赫兹接触模型的基础上发展了粘合力学模型——JKR模型［17］。JKR模型把表面能γ考虑进去，力f和位移δ之间的关系由参数的形式给出［17］

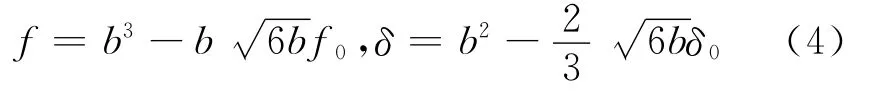
其中b为微接触面半径；f0和δ0为归一化常数，f0＝πrγ，δ0＝ （3πγ（1－ν2）／（2E）。

图2为JKR模型的力学描述，其力－位移关系考虑了微观粘合滞后。图2中的作用力可以分为滞后力fH（纯矩形框）和非滞后力fNH（纯赫兹曲线）两部分。当从大的负扰动值增加位移时，没有接触也没有力。直到位移是零的时候，接触突然出现，力为负值，那是粘着吸力。对于正扰动值，接触依然存在，这时候遵循赫兹型接触定律。反过来，当从大的正扰动值减小位移到小于0时，粘着吸力并没有消失，直到某个临界值时力才又回归到0。滞后转换的方向如箭头所示，其力－位移曲线的典型行为是滞后的。

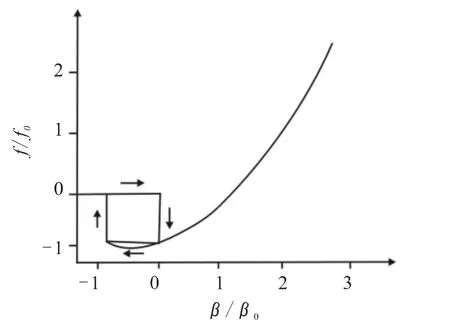
图2 JKR接触模型的本构关系Fig.2 The constitutive relation of JKR contact model.

上世纪90年代，Tutuncu等人指出传统的理论在高围压下实验结果和理论有明显的偏离，用粘合滞后来解释滞后和能量损失［18，8］。即使是接触部分受到强烈的挤压，颗粒间的摩擦仍然是很小的。

2 孔隙流体的作用

流体的存在极大地影响了岩石的线性特征（声速、能量损失），这些效应在唯象Biot理论框架中要经常考虑到，Biot理论提供了最好的定量描述［19］。Khanzanehdari和Sothcott［20］通过声学装置测量了砂岩的动态体积模量和剪切模量，观察到动态剪切模量随流体饱和而引起的变化与饱和流体的类型和粘滞性、岩石的微结构和施加压力有密切的关系，认为粘滞耦合、自由表面能的减少以及局部和全局流动引起的频散是造成动态剪切模量随流体饱和而变化的原因。

岩石的非线性弹性显著地受到孔隙流体存在的影响［8，21－27］。下面简单地讨论一下基于湿赫兹接触的非线性模型。最简单的例子是颗粒间的空间100%充满了流体（100%饱和），这时流体对颗粒接触提供了额外的弹性效应，其状态方程（忽略原子流体的非线性）具有以下的形式［22］

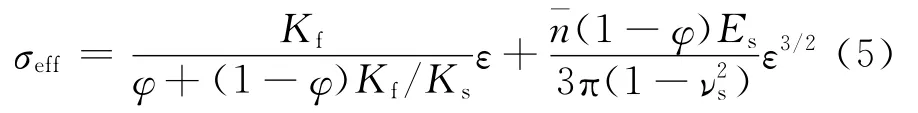
其中Kf和Ks分别是液相和固相的体积模量；φ是孔隙率。关系式（5）预测了在整个介质中非线性会降低，但是它只应用于接近100%流体饱和的情况。这是很自然的：水填充到孔隙中会使材料变硬［26－27］。但是，对于相对小的饱和度（比如小于30%），非线性反而会增加［26－27］，因为这时还要考虑毛细和偶极作用力对颗粒耦合的影响。为了描述这种效应，似乎有必要考虑由于颗粒之间的薄液膜而作用在颗粒上的力。Tutuncu和Sharma从热力学的观点出发，具体地考虑了这些力的作用，他们的预测与声波速和衰减测量是相当符合的［23］。

席道瑛等［24］认为，岩石孔隙流体的粘滞性对滞后现象有影响。在循环外力作用下，存在于颗粒接触面之间的孔隙流体将产生震荡运动，而粘滞性大的流体不容易在孔隙岩石中流动，因而其滞后程度会大一些。Tutuncu等认为孔隙流体的化学特性对岩石内部的粘滑移动和颗粒接触粘合滞后有明显的影响［8］。基于流体－蒸汽平衡的理论，Van Den Abeele等［25］开展了流体对粘结系统作用的研究。对于小于微米级的孔隙尺度来说，流体的影响是很强烈的，并用PM空间滞后单元解释了少量水的宏观效应。

3 Granato—Lucke模型

在很多的滞后材料里，粘结系统是晶体的，这样粘结系统的晶格内部的位错能令人信服地产生非线性响应。早在1956年，Granato和Lucke（GL）就建议了一个基于金属位错的物理模型。为了描述弹性变形，他们在牵住了杂质原子的一段位错线和细绳的运动之间做了模拟（图3（a））。当应力增加时（通常是剪切应力），位错象一条条细绳一样产生变形，直到在某个临界应变时它们从晶体结构节点之间的所有杂质原子中分离出来。结果物质变得更软，从而导致了应力－应变有关的强烈的非线性（图3（b）中的实线）。这个过程在原子尺度上是不可逆的：在减小的应力作用下，系统将沿着"软"线回到平衡位置。然而，导致的平衡状态在诱发位错起作用的前后可以是相同的。这个模型也体现了慢动力现象，这是因为平衡状态需要一些时间才能恢复。实际上，粘结点之间的长度是统计分布的，使得滞后回线变光滑（图3（b）中的虚线）。GL模型的混合模型包括了其它方面的特征如频率依赖性。尽管有一些不足，这个模型确实是滞后动力行为方面一个开拓性的微观模型。

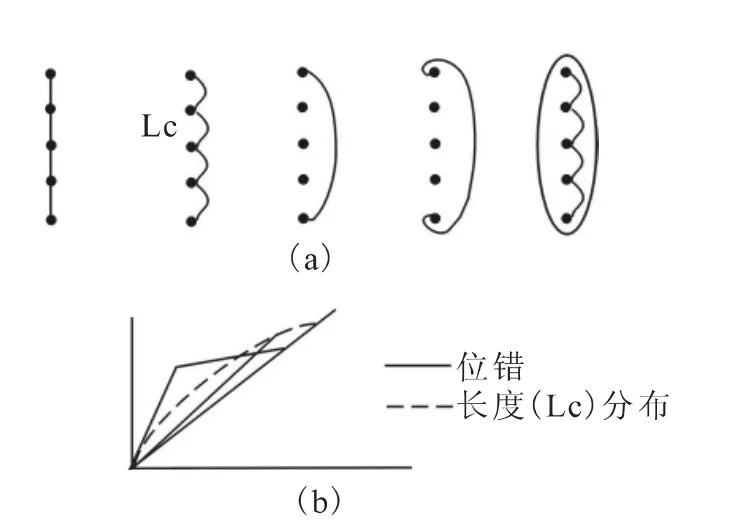
图3 绳形位错的Granato－Lucke模型Fig.3 Granato－Lucke model of string－like dislocations.

如果我们考虑一个三角形应力－应变曲线（图3（b）），每个单元（细绳）具有给定的应变，那么在相关平面上几乎是一个直角三角形回线。这与后面提到的PM空间很相似。确实，如果我们有这些元素的分布，就可以得到与PM空间模型相同的缩放比例（直角三角形而不是矩形）。这意味着PM空间模型中的HMU（滞后细观单元）可以定性地类似于GL位错，颗粒之间的接触面具有切线变形。

对于岩石而言，位错的作用还不是明显的。对于一些含非晶质粘结材料如硅土，位错并不存在。而对于像方解石之类的晶体材料，位错还是存在的。从能量的角度来说，位错机制的尺度正好是非线性响应机制的尺度。

4 PM模型——联系微观和宏观的桥梁

在微观物理机制和宏观力学现象之间，往往缺乏一个沟通的中间环节，使得从微观物理机制的假设中推导得到的结果与宏观力学现象存在较大的偏离，有时甚至完全不能解释一些宏观力学现象。因此，在微观和宏观之间，有时需要细观作为过渡和沟通的桥梁。

PM模型就是一个基于岩石细观尺度的唯象模型。PM模型的主要思想是系统内存在大量的具有滞后性的小单元，这些小单元在性质上有一定的分布规律，其自身的变化过程共同影响系统并使系统产生非线性滞后效应。这就是滞后细观单元（HMU），它实际上是岩石中存在的微裂隙、连接点、接触面、颗粒边界等复杂的结构特征的抽象简化。每个个体的HMU的具有一对数值σ0和σc，分别代表打开和关闭应力。如图4所示，对于某个给定的HMU，从给定的压力数值σ＜σc开始，我们假定状态变量r＝1，一直保持这种状态，直到σ＝σc时r变为0；但是，当σ从大于σc的数值减少到σ0时，状态变量r却沿着另外的路线返回，即r一直保持为0，直到σ＝σ0时才又变为1。这样，HMU是滞后的，对不同的打开和闭合应力产生响应，因此单元和作为整体的系统的弹性响应依赖岩石的应力历史。

图4 HMU的滞后示意图Fig.4 Sketch of HMU hysteresis.

一个应力σc时闭合，σ0时打开的HMU位于PM 空间中的点（σc，σ0），设在某个应力σ作用下处于状态变量r＝0的HMU占整个HMU数目的比例为n（E），则相应的应变为［26］

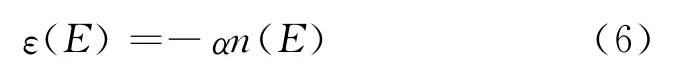
其中α为与细观弹性材料有关的常数［6］，这就是具有滞后回线和离散记忆的应力－应变状态方程。

岩石滞后非线性的物理机制的探究主要集中于岩石内部的粘结系统。PM模型可以把准静态数据与声速数据（动态应力－应变数据）联系在一起，也就是说，从准静态得到的模量可以用来预测动态模量［27］。通过岩石内部的粘结系统的统计描述，把准静态与动态数据联系了起来。粘结系统被模拟为具有复杂弹性特性的细观弹性单元的系统，这种复杂弹性特性由实验数据所确定，而细观弹性单元与赋予岩石特性的物理机制之间的关系有待建立。

PM模型可以解释岩石的滞后和离散记忆等传统非线性理论难以解释的现象。PM模型不仅能逼真地模拟各种形态的应力－应变曲线、“X”形切线模量和泊松比以及离散记忆特征［5］，描述岩石的静态模量和动态模量之间的关系［29］，了解多孔岩石自适应调整的频率和温度效应［30］，而且可以用来解释孔隙流体在波传播中的影响［25］。在地震波的非线性弹性传播研究中，PM模型已经成为描述孔隙介质的非线性现象的重要工具。同时它对理解岩石滞后非线性的机制和尺度是很重要的。

5 结语

上述细观非线性模型可以作为描述岩石和其他固结颗粒材料的非线性声学特性的基础，给出了强非线性和非经典现象的解释。赫兹接触模型是具有多尺度和滞后特性的经典模型，它预测了岩石中强烈的非线性；软的粘结系统几乎决定了岩石的力学性质，粘结系统中的流体对非线性响应的贡献特别显著，但是目前还没有搞清楚粘结系统和和孔隙流体究竟是如何影响非线性响应的；GL模型是一个基于金属位错的物理模型，这是滞后动力行为方面一个开拓性的微观模型，但是在应用于岩石力学非线性行为的时候还需慎重，因为并非所有岩石的位错作用都是明显的；PM模型是一个基于岩石细观尺度的唯象模型，它对理解岩石滞后非线性的机制和尺度是很重要的。此外，现实情况是非常复杂的，实际材料的细观非线性的物理理论需要更深入的研究。

［1］Guyer R A，Johnson P A.Nonlinear mesoscopic elasticity：evidence for a new class of materials［J］.Physics Today，1999，52：30－36.

［2］Guyer R A，TenCate J，Johnson P.Hysteresis and the dynamic elasticity of consolidated granular materials［J］.Physical Review Letters，1999，82（16）：3280－3283.

［3］Johnson P A，McCall K R.Observation and implications of nonlinear elastic wave response in rock［J］.Geophysical Research Letters，1994，97.

［4］许江，鲜学福，王鸿，等.循环加、卸载条件下岩石类材料变形特性的实验研究［J］.岩石力学与工程学报，2006，25（S1）：3040－3045.

［5］陈运平，刘干斌，姚海林.岩石滞后非线性弹性模拟的研究［J］.岩土力学，2006，27（3）：341－347.

［6］陈运平，席道瑛，薛彦伟.循环荷载下饱和岩石的滞后和衰减［J］.地球物理学报，2004，47（4）：672－679.

［7］陈运平，王思敬，王恩志.岩石应力－应变滞后现象的定量研究［J］.岩石力学与工程学报，2007，26（S2）：4066－4073.

［8］Tutuncu A N，Podio A L，Gregory A R，et al.Nonlinear viscoelastic behavior of sedimentary rock，PartⅠ：Effect of frequency and strain amplitude［J］.Geophysics，1998，63：184－194.

［9］Tutuncu A N，Podio A L，Gregory A R，et al.Nonlinear viscoelastic behavior of sedimentary rock，part II：hysteresis effects and influence of type of fluid on elastic moduli［J］.Geophysics，1998，63（1）：195－203.

［10］TenCate J A，Smith D E，Guyer R A.Universal slow dynamics in granular solids［J］.Physical Review Letters，2000，85：1020.

［11］TenCate J A，Shankland T J.Slow dynamics in the nonlinear elastic response of Berea sandstone［J］.Geophysical Research Letters，1996，23：3019.

［12］TenCate J A，Pasqualini D，Habib S.Nonlinear and Nonequilibrium Dynamics in Geomaterials［J］.Physical Review Letters，2004，93（6）：065501／1－4.

［13］Landau L D，Lifshitz E.Theay of elasticity，（3rd edition）［M］.Oxford：Pergamon Press，1986.

［14］Walsh J B.Seismic wave attenuation in rock due to friction［J］.Journal of Geophysical Research，1966，71：2591－2599.

［15］Mavko G M.Frictional attenuation：An inherent amplitude dependence［J］.Journal of Geophysical Research，1979，84：4769－4775.

［16］Mason W P.Internal friction mechanism that produces an attenuation in the earth＇s crust proportional to the frequency［J］.Journal of Geophysical Research，1979，84，4963－4966.

［17］Johnson K L，Kendall K，Roberts A D.Surface energy and the contact of elastic solids［A］∥Proc.R.Soc.Ser.A ［C］.London：［s.n.］，1971，324，301.

［18］Sharma M M，Tutuncu A N.Grain adhesion hysteresis：a mechanism for attenuation of seismic waves［J］.Geophysical Research Letters，1994，21（21）：2323－2326.

［19］Wilmanski K.A few remarks on Biot＇s model and linear acoustics of poroelastic saturated materials［J］.Soil Dynamics and earthquake engineering，2006，26：509－536.

［20］Khanzanehdari J，Sothcott J.Variation in dynamic elastic shear modulus of sandstone upon fluid saturation and substitution［J］.Geophysics，2003，68（2）：472－481.

［21］Zinszner B，Johnson P A，Rasolofosaon P N J.Influence of change in physical state on elastic nonlinear response on rock：Significance of effective pressure and water saturation［J］.Journal of Geophysical Research，1997，102：8105－8120.

［22］Belyaeva I，Zaitsev V，Ostrovsky L.Nonlinear acoustoelastic properties of granular media［J］.Acoustical Physics.1993，39（1）：11－14.

［23］Tutuncu A N，Sharma M M.The influence of fluids on grain contact stiffness and frame moduli in sedimentary rocks［J］.Geophysics，1992，57（12）：1571－1582.

［24］席道瑛，陈运平，陶月赞，等.岩石的非线性弹性滞后特征［J］.岩石力学与工程学报，2006，25（6）：1086－1093.

［25］Van Den Abeele K E A，Carmeliet J，Johnson P A，et al.Influence of water saturation on the nonlinear elastic mesoscopic response in earth materials and the implications to the mechanism of nonlinearity［J］.Journal of Geophysical Research，2002，107（B6）：4－11.

［26］席道瑛，杜赟，易良坤，等.液体对岩石非线性弹性行为的影响［J］.岩石力学与工程学报，2009，28（4）：687－696.

［27］杜赟，席道瑛，徐松林，等.岩石非线性细观响应中孔隙液体的影响［J］.岩石力学与工程学报，2010，29（1）：209－216.

［28］McCall K R，Guyer R A.Equation of state and wave propagation in hysteretic nonlinear elastic materials［J］.Journal of Geophysical Research，1994，99：23887－23897.

［29］Guyer R A，McCall K R，Boitnoitt G N，et al.Quantitative implementation of Preisach－Mayergoyz space to find static and dynamic elastic moduli in rock［J］.Journal of Geophysical Research，1997，102：5281－5293.

［30］席道瑛，徐松林，李廷，等.岩石中微细观结构对外力和温度响应的概率研究［J］.岩石力学与工程学报，2007，26（1）：15－21.

［31］任隽，朱元清，秦浩文.上海地震台阵标定及结果分析［J］.西北地震学报，2002，24（4）：325－329.

［32］任隽，陈运平，潘纪顺，等.海南岛及其近海中强地震前加卸载响应比的变化特征［J］.西北地震学报，2005，27（1）：71－74.

［33］郭晓，张元生，何斌.兰州市及其附近地区介质衰减特征研究［J］.西北地震学报，2010，32（3）：244－247.

［34］唐益群，崔振东，王兴汉.密集高层建筑群的工程效应引起地面沉降的初步研究［J］.西北地震学报，2007，29（2）：105－108.

［35］杨庆华，姚令侃，邱燕玲，等.高烈度地震区岩土体边坡崩塌动力学特性研究［J］.西北地震学报，2011，33（1）：34－39.