基于极限平衡条件的土体局部稳定分析①

2011-01-25邵龙潭刘士乙

地震工程学报 2011年3期

邵龙潭，刘士乙

（大连理工大学工业装备结构分析国家重点实验室，辽宁大连 116085）

0 引言

岩土结构的失稳破坏是岩土工程建设中经常遇到的主要灾害之一。一般情况下，失稳破坏都是由局部破坏逐渐扩展以致贯通形成滑面的渐进过程。因此土体结构的局部稳定分析对于研究土体结构的稳定性具有参考价值。

目前，边坡、地基和支挡结构的稳定分析主要采用极限平衡法和有限元法［1－2］。极限平衡法假定土体是理想塑性体材料，不考虑土体内部的应力－应变关系，无法模拟土体由局部破坏发展至整体破坏的渐进破坏过程。有限元法完全克服了上述缺点，在土体的渐进破坏分析方面成为主要的工具。

王庚荪［3］采用接触单元模拟滑面上的接触摩擦状态，进而模拟边坡的渐进破坏过程，但要事先假定滑面位置。唐洪祥和李锡夔［4］基于压力相关弹塑性Cosserat连续体模型的有限元，模拟了挡土墙和开挖边坡的渐进破坏过程。王庚荪、孔令伟等［5］应用含剪切带单元和破坏面自动寻踪技术模拟了边坡的渐进破坏过程。

土体的破坏型式主要为剪切破坏。土的摩尔－库仑强度理论指出：在一定压力范围内，土的抗剪强度可以用库仑公式表示，当土体中一点任一平面上的剪应力达到土的抗剪强度时，就认为该点发生剪切破坏。当土体内一点出现剪切破坏时，也称该点处于极限平衡状态。此时从应力角度来说，该点处于极限状态，从力的平衡角度来说，该点剪切破坏平面微元面积上的土体内力达到极限平衡，即微元土体在破坏平面上的剪切力等于抗剪力。一点（某一方向上）的剪应力等于抗剪强度，就是土体的强度条件，或者称为极限平衡条件。

将土体一点的极限平衡条件推广，可以得到土体沿任一曲面局部或者整体的极限平衡条件。文献［6］证明了当土体整体沿曲面的剪应力和抗剪强度的积分值（代数和）相等时，土体整体沿该曲面达到极限状态，并由此给出土体稳定安全系数的定义，说明其物理意义是土体沿曲面整体达到极限平衡时的平均强度折减系数或强度储备系数。

本文进一步将摩尔－库伦强度理论推广到土体内的任意局部曲面，就平面问题给出土体在局部曲面上的极限平衡条件，以此为判据，根据有限元应力分析结果，当土体沿某一局部曲面达到极限平衡时，则认为土体在这一局部曲面上出现剪切破坏。搜索确定这一曲面的扩展过程可以确定土体的渐进破坏过程。

1 土体局部的极限平衡条件

文献［6］说明了土体沿任意曲面l整体达到极限平衡的充分必要条件是

该条件也可以推广到土体内任意曲面的局部。

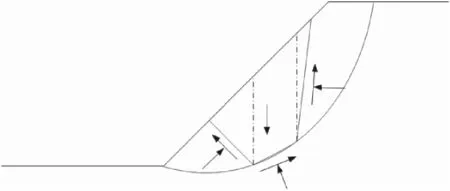
图1 局部曲面上任意形状脱离体平衡示意图Fig.1 Sketch of balance of forces and moments exerted on soil mass along part curved surfaces.

局部曲面上的土体达到极限平衡状态同样是指在局部曲面上土体滑动力的合力与阻滑力的合力相等，并且对曲面外任意一点滑动力矩与阻滑力矩相等。只要我们认识到，当局部曲面上土体的滑动力与阻滑力相等时，由此曲面向土体边界所取的任意形状脱离体，都会满足平衡条件，如图1，那么土体沿局部曲面l的极限平衡条件∫τfdl＝∫τdl的证明与沿曲面整体达到极限平衡条件的证明相同，可以参见文献［4］，这里不再赘述。

由此，同样可以定义土体沿局部曲面的抗滑稳定安全系数，公式与整体相同。

2 基于极限平衡条件的渐进破坏分析

由土体的极限平衡条件，定义安全系数K作为土体内部任意曲面（包括微元长度、局部曲面和整体曲面）是否达到极限平衡状态的准则：

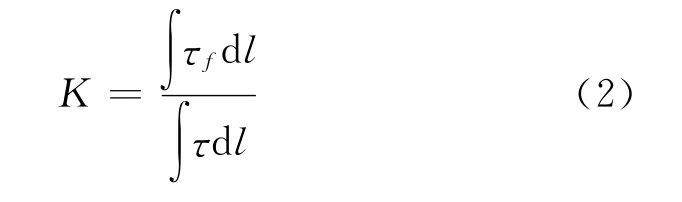
若｜K－1.00｜≤ε，ε是反映计算误差的一个小量（本文算例取为0.05），则认为土体沿曲面（局部或整体）达到极限平衡状态。

土体的渐进破坏一般是伴随加载过程或者土的强度降低而发生的。采用弹塑性或非线性弹性（非线性弹性时要考虑应力调整）有限元法计算土体结构的应力，根据每一次的应力计算结果计算沿局部或整体曲面的安全系数，当安全系数接近于1时，认为达到极限平衡状态。

搜索确定土体内达到极限平衡状态的曲面仍然采用文献［6］中介绍的方法：即将待搜索的曲面（线）离散，以直线线段连接相邻的节点近似地代表曲面（线），搜索节点坐标确定曲面（线）。求解时在拟定的搜索区域内给定合适数量的x坐标（为保证破坏曲面平滑，可以密一些），在每一个x坐标对应的平行于纵坐标轴的直线上滑动纵坐标y，以节点的yi为搜索变量。

以土体结构的逐级加载过程为例，为了确定渐进破坏过程，对于每一级荷载先以连接每一个相邻节点的微小线段作为局部曲面，逐一计算每一个线段上的土体安全系数，当满足│K－1.00│≤ε时即认为出现剪切破坏，标志出剪切破坏的线段。在进行下一级荷载计算时，除逐一计算每一个线段上的土体安全系数外，再把安全系数计算扩展到每两个相连的线段，同样以│K－1.00│≤ε为标准判断是否出现剪切破坏，以此类推，直到发生整体破坏为止。

3 算例举例

3.1 均质边坡

某均质边坡如图2所示，坡高H＝20m；内摩擦角φ＝17°；土体容重为20kN／m3；粘聚力c＝42 kPa；E＝10MPa；v＝0.3；坡角为40°。距坡顶20m作用均布荷载，递增荷载P 分别为0、50、75、85、100、150、160、170、175kPa。

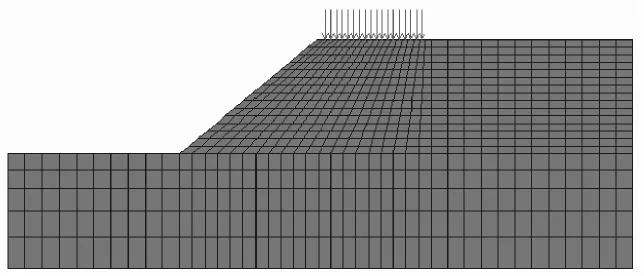
图2 某边坡有限元网格划分Fig.2 Mash of FEM model for a slope.

取坡体底边界为固定约束，左右边界为水平约束，其它边界自由。

本文基于非关联流动法则，采用与M－C准则精确匹配的D－P准则计算边坡的应力场。

图3（图版Ⅰ图3）给出随外荷载递增所产生的达到极限平衡状态的曲面微元及局部或整体曲面。坡角处最先出现达到极限平衡状态的区域，随荷载增加，极限平衡状态的区域逐步扩展。当荷载为175kPa时，滑动面贯穿整个边坡，对应的安全系数为1.03。滑动面的形状与位置与ANSYS计算所得的等效塑性应变区域基本一致。

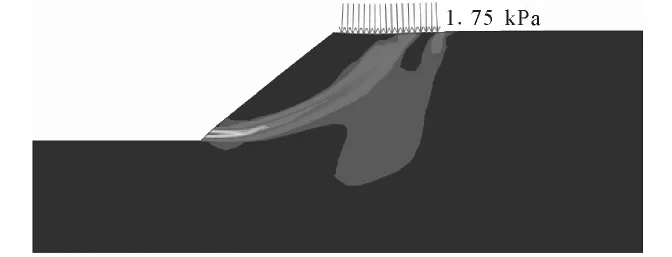
图4 由ANSYS计算的等效塑性应变分布Fig.4 Equivalent plastic strain distribution from ANSYS.

3.2 地基极限承载力

在经典塑性力学中，岩土体材料假定为无重的理想弹塑性体，在此基础上可以得到一系列的解析解（理论解）。

对于图5所示的地基，宽30m；深15m；荷载作用宽度为2m；地基底边边界为固定约束，左右边界为水平约束。取c＝10kPa；φ＝10°；弹性模量E＝30000kPa；泊松比v＝0.3；递增荷载P分别为40、50、60、70、80、83、83.5kPa。

同样基于非关联流动法则，采用与M－C准则精确匹配的D－P准则计算地基的应力场。

图5 某地基有限元网格划分Fig.5 Mash of FEM model for a foundation.

图6（图版Ⅰ图6）给出随外荷载递增所产生的达到极限平衡状态的曲面微元及局部或整体曲面。达到极限平衡状态的区域逐步向下扩展，但由于下部两侧土体的约束并无向下的带状贯通区域。荷载由70kPa增加至83.5kPa时，逐步形成带状的极限平衡状态的区域，即滑动面或剪切带。极限荷载83.5kPa为Prandtl理论解，与本文所得结果一致。滑动面的形状与位置与ANSYS计算所得的等效塑性应变区域及Prandtl解也一致。