像素相位误差的特性*
2011-01-25曹西平彭青玉张庆丰
曹西平,彭青玉,张庆丰
(1.暨南大学计算机科学系,广东 广州 510632;2.暨南大学,中法天体测量、动力学与空间科学联合实验室,广东 广州 510632;3.广东省高等学校光电信息与传感技术重点实验室(暨南大学),广东 广州 510632)
根据Stone[1]的研究,在高斯函数拟合过程中为了避免像素相位误差,星像在半高全宽(FWHM——Full Width at Half Maximum)下最好大于4 pix。然而,无论是地面成像还是空间成像,均可能存在星像在半高全宽下小于4 pix的情况。例如,在地面观测中,美国海军天文台使用的双筒照相仪得到的图像就是欠采样的,从他们发布的UCAC(The US Naval CCD Astrograph Catalog)系列星表中[2-4]可以看到。他们虽然采用了不同模型对CCD图像中的星像进行拟合[5],但像素相位误差依然存在。在空间观测中,Hubble空间望远镜WFPC2照相机的欠采样成像也是一个明显的例子。而且,由于这种欠采样,曾困扰Hubble望远镜高精度天体测量工作长达10年之久。Anderson和King提出了有效点扩散函数(ePSF-effective Point——Spread Function)新概念[6],并利用抖动的图像序列提取精确的ePSF,基本上解决了Hubble望远镜图像欠采样的问题。然而,Anderson本人也承认求解ePSF的复杂性。当图像足够采样时,ePSF拟合法与经典的高斯拟合法相比,不会有精度上的增益。
为了更深刻地认识像素相位误差对天体测量的影响,在生成仿真图像上利用高斯函数作为点扩散函数模型,探究了影响像素相位误差的决定因素,也分析了像素相位误差对位置测量精度的影响。
1 像素相位误差与ePSF的概念
1.1 像素相位误差
像素相位是星像中心相对于像素边界的位置,方向的像素相位可分别定义为φ(x)=x-int(x+0.5),φ(y)=y-int(y+0.5),(x、y分别为星像中心的横坐标,纵坐标)。采用文 [6]中的图来说明像素相位误差是如何产生的。图1显示的是两个不同的点扩散函数(PSF)模型拟合相同的一维欠采样星像轮廓,这个星像轮廓由一个直方图表示,其中包含星像中心的3 pix。图中可以看出同样精确拟合星像轮廓的两个不同的点扩散函数模型拟合出的星像中心有明显差异,达到0.07 pix,这个偏差就是像素相位误差。
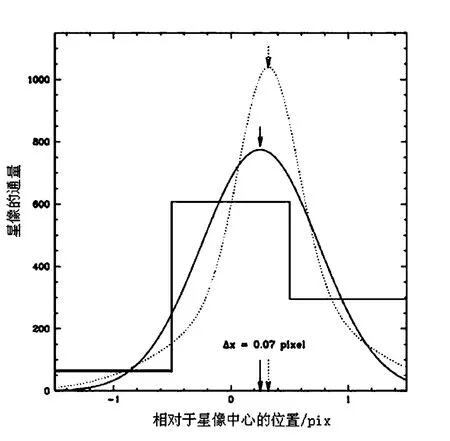
图1 这个直方图显示欠采样的一维星像轮廓最中心3 pix的灰度。实线表示纯粹的高斯模型拟合结果,虚线表示较为尖锐的高斯模型拟合结果,并且拟合的范围较大。箭头显示了这两个高斯模型在峰值的位置上相差0.07 pix(原图来自文[6])Fig.1 Flux distribution int the x-direction cross section through the center of a stellar profile.The histogram shows the pixel values for the innermost 3 pixels of the underampled one-dimensional stellar profile.The solid curve is the fit with a pure Gaussian model.The dotted curve is the fit with a sharper Gaussian for a broader range(adopted from Ref[6])
1.2 ePSF的概念
为解决Hubble空间图像欠采样的问题,美国学者Anderson和King提出了ePSF的概念[6]。假如一个星像中心位于(xc,yc),(i,j)是该星像周围的一个像素,它们与ePSF存在如下关系,

其中pij为像素(i,j)的灰度值;S*为天空背景值;f*为星像的通量因子; ψE(Δx,Δy)=ψE(i-xc,jyc)为点(i,j)相对于星像中心的有效点扩散函数值(ePSF)。
(1)式的提出给仿真图像的生成带来了很大方便,不必像Stone[1]那样在一个像素范围内进行积分求得该像素的灰度值,而只需要利用(1)式进行简单的计算就可以生成像素点 (i,j)处的灰度值。本文正是基于ePSF的概念,生成所有的仿真图像。
2 高斯函数模型与仿真图像的生成
2.1 高斯函数模型
用高斯函数(Gaussian)模型描述星像轮廓:

I(x,y)为像素(x,y)处的灰度值;H是高斯函数的峰值;B为天空背景;(xc,yc)是星像中心的坐标位置;R为高斯函数的标准差,它与大气视宁度有关。R与星像的半高全宽(FWHM)存在如下关系:

比较(1)式和(3)式发现,ePSF和Gaussian存在如下关系:
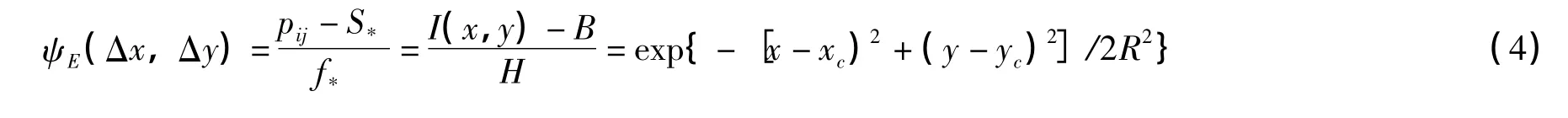
2.2 生成仿真图像
对仿真图像,采用2k×2k的分辨率。生成仿真图像的主要步骤如下,首先设置图像的高度、宽度及调用CFITSIO库[7]创建背景图像。然后在背景图像中通过设置星像的中心位置、通量、半高全宽来添加星像,其中星像采用高斯模型(式2)。最后对图像添加泊松噪声。图2是仿真图像的一部分。
3 影响像素相位误差的决定因素
这里生成的星像半高全宽都为1.5 pix的50幅仿真图像,其中每幅图像添加像素相位随机的200颗亮星。采用亮星的目的是亮星具有很高的信噪比,可以更好地观察像素相位误差的影响。
现在采用高斯函数(式2)来实验分析什么是影响像素相位误差的决定因素及怎样获得精确的高斯函数模型。高斯函数拟合过程中,如果标准差R不参与迭代,R为固定值,大小为设置的初值,这时拟合只需求解B、H、xc、yc4个参数。如果R参与迭代,则求解的参数有5个,分别是B、H、xc、yc、R。

图2 生成仿真图像的一部分Fig.2 A part of the simulated image
3.1 R不参与迭代
迭代拟合求4个参数B、H、xc、yc的解。它们的初始值分别设为B0、H0、x0、y0,其中x0、y0是目标框(圈定星像的矩形框)内最大灰度值的坐标位置,B0是目标框内的最小灰度值,H0是目标框内最大灰度值与最小灰度值之差。在迭代过程中有下述关系:xc=xc+Δx,yc=yc+Δy,B=B+ΔB,H=H+ΔH。等式中所求得的参数值只是某次迭代过程中的值,并不是各个参数的确切值。要得到较为准确的值,需要多次迭代。迭代求解结束的条件是: |Δx|<0.001,|Δy|<0.001,|ΔB|<0.01,|ΔH|<0.01。在实验过程中对高斯函数标准差R分别设置5个初值,R1=FWHM0/2.40(FWHM0为星像的半高全宽1.5)、R2=FWHM0/2.38、R3=FWHM0/2.35、R4=FWHM0/2.33、R5=FWHM0/2.30。
针对上述R的不同取值,通过观察这50幅仿真图像计算出每个星像的残差(xc-x0,yc-y0),每幅图像200颗星,即总共有10000个残差,用这些残差描述像素相位误差。用图3~7表示像素相位误差相对于像素相位的变化,其中横轴是x、y方向的像素相位,纵轴是对应方向的像素相位误差。

图3 R1=FWHM0/2.40,模型的半高全宽相对于星像真实的半高全宽偏小,残差总体上先负后正Fig.3 Fitting residuals of stellar positions for R1=FWHM0/2.40,under which the model FWHM are less than the true FWHM.The residuals overall have the same signs as pixel phases
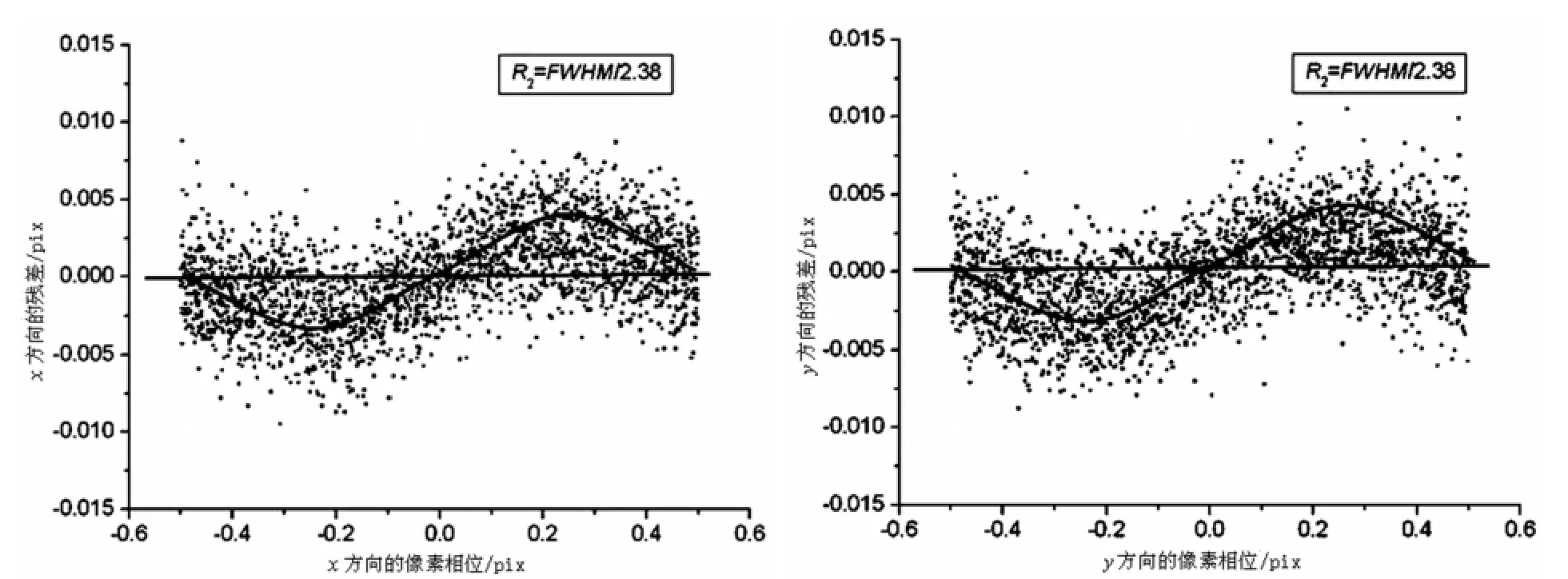
图4 R2=FWHM0/2.38,模型的半高全宽相对于星像真实的半高全宽也是偏小Fig.4 Fitting residuals of stellar positions for R2=FWHM0/2.38,under which the model FWHM are again less than the true FWHM
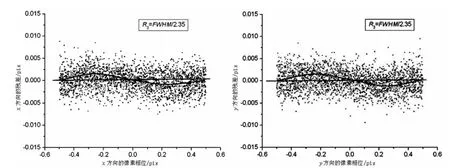
图5 R3=FWHM0/2.35模型的半高全宽与星像真实的半高全宽最接近,残差最小Fig.5 Fitting residuals of stellar positions for R3=FWHM0/2.35,under which the model FWHM are closest to the true FWHM and the residuals reach minima
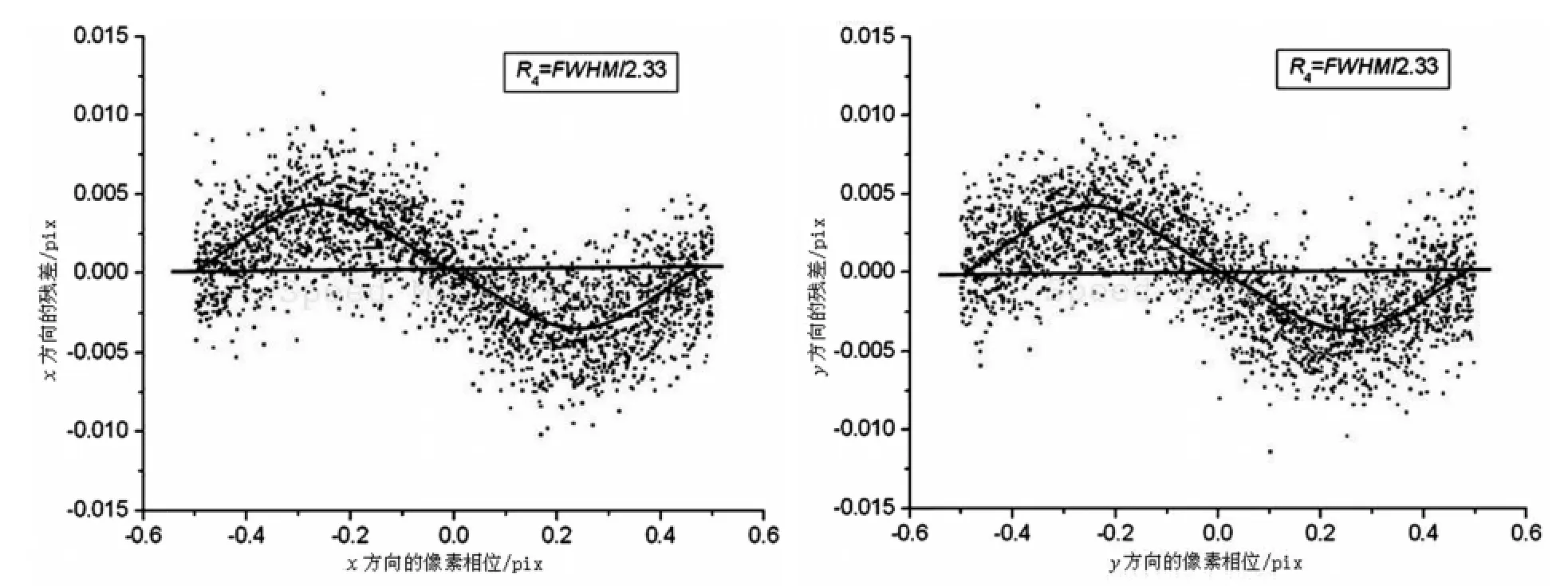
图6 R4=FWHM0/2.33模型的半高全宽相对于星像真实的半高全宽偏大,残差总体上先正后负Fig.6 Fitting residuals of stellar positions for R4=FWHM0/2.33,under which the model FWHM are larger than the true FWHM.The residuals overall have an anti-correlation with the pixel phases

图7 R5=FWHM0/2.30模型的半高全宽相对于星像真实的半高全宽也是偏大Fig.7 Fitting residuals of stellar positions for R5=FWHM0/2.30,under which the model FWHM are again larger than the true FWHM
实验发现,模型的半高全宽是影响像素相位误差的决定因素,当模型的半高全宽越接近星像真实的半高全宽时,像素相位误差越小。图5显示出高斯模型的半高全宽与星像真实的半高全宽偏差最小时,像素相位误差也最小。把图3~7的像素相位误差幅度的平均曲线见图8。其中R1、R5分别表示高斯模型的半高全宽相对于星像真实的半高全宽偏小与偏大的情况,它们对应曲线的幅度很大且相位相差180°。
另外还发现x方向的像素相位误差只受x方向的像素相位影响,而与y方向的像素相位没有关系,反之亦然。取R5=FWHM0/2.30的情况进行实验发现,y方向的像素相位误差对于x方向的像素相位是随机分布的(图9左),x方向的像素相位误差对于y方向的像素相位也是随机分布的(图9右)。
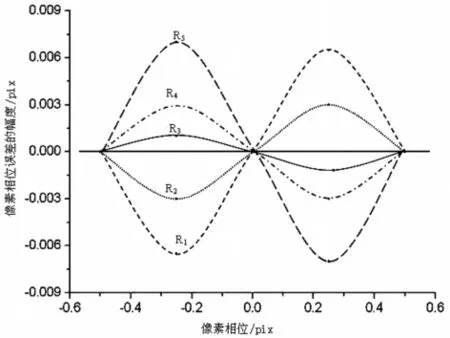
图8 横轴为像素相位,纵轴为像素相位误差的平均值。其中R1、R5的情况是模型的半高全宽相对星像真实的半高全宽偏得较大,此时像素相位误差的幅度也很大。R3是几个值中偏得最小的,此时像素相位误差幅度也最小Fig.8 Average pixel-phase error versus pixel phase in the x direction.The R1and R5cases are those large with large deviations of the model FWHM from the true FWHM and amplitudes of pixel-phase error variations.In the R3case,the model FWHM are closest to the true FWHM and the amplitude of pixel-phase error variation reaches minimum
3.2 参与迭代
此时迭代拟合要求解B、H、xc、yc、R这5个参数。与R不参与迭代情况唯一不同的是R的最终解是进行多次迭代后的结果,而不仅仅是设置初值。设R的初始值为FWHM0/2.30,且R退出迭代的条件是<0.001。每迭代一次,高斯函数的标准差就趋近于星像真实的标准差FWHM0/,经过几次迭代之后,两者大小几乎相等,也就是迭代后的高斯模型半高全宽几乎和星像真实的半高全宽相等。实验发现,R参与迭代的高斯拟合效果非常好,残差很小(图10)。可见,拟合模型精确与否取决于模型的半高全宽与星像真实的半高全宽是否趋于相等。
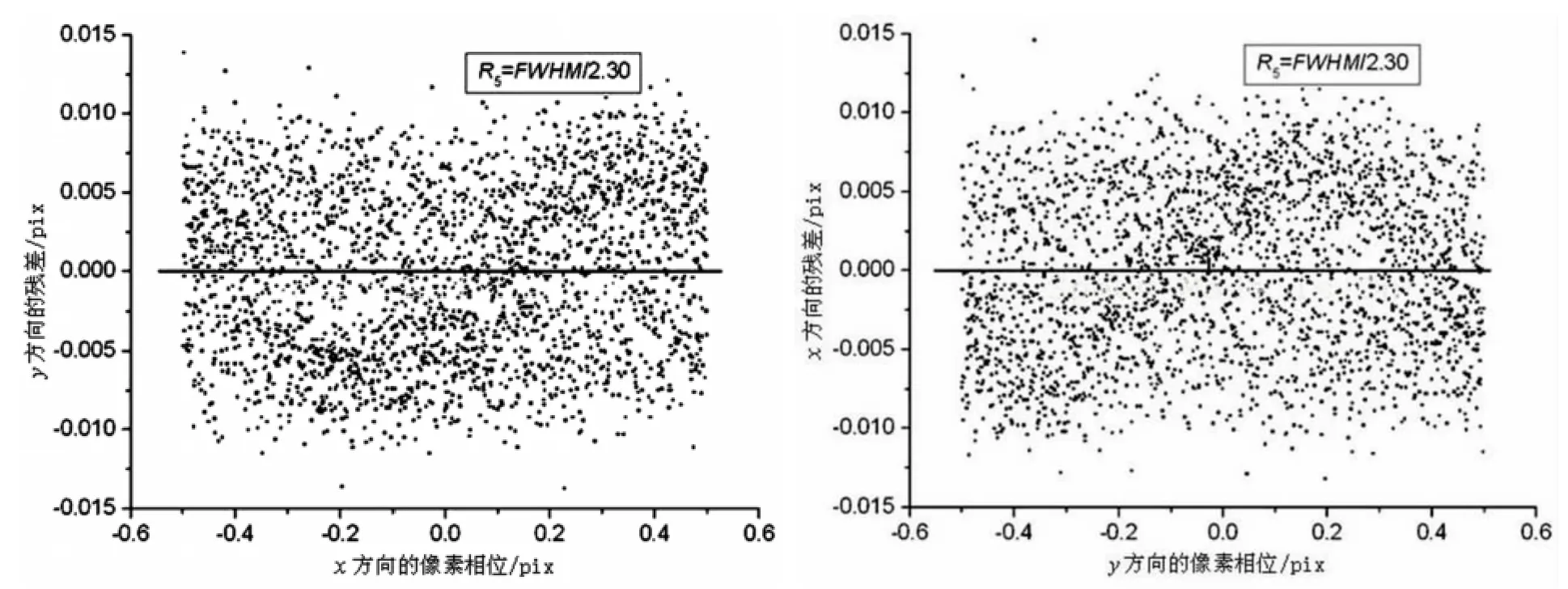
图9 (a)y方向的残差关于x方向像素相位的函数(b)x方向的残差关于y方向像素相位的函数Fig.9 (a)Residuals of y positions versus x pixel phases(b)Residuals of x positions versus y pixel phases
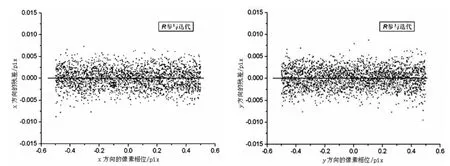
图10 参与迭代的高斯拟合效果(a)x方向的残差关于x方向像素相位的函数 (b)y方向的残差关于y方向像素相位的函数Fig.10 Results of Gaussian fitting with our iterative approach involving the R parameter.(a)Residuals of x positions versus x pixel phases (b)Residuals of y positions versus y pixel phases
4 像素相位误差的幅度与星像半高全宽之间的关系
和上节生成图像的情况不一样,生成星像的半高全宽分别是 1.4、1.5、1.6、1.7、1.9、2.0、2.3、2.5、2.7、3.0的一系列仿真图像。采用不精确的高斯函数模型(标准差R不参与迭代,其大小为FWHM0/2.30)来实验分析不同半高全宽下像素相位误差幅度的大小。实验发现,像素相位误差的幅度随着星像半高全宽的增大而变小,当半高全宽大于2 pix,像素相位误差的幅度几乎为0(图11)。可见,在星像的半高全宽大于2 pix,高斯拟合法无论标准差精确与否都不再受像素相位误差的影响。
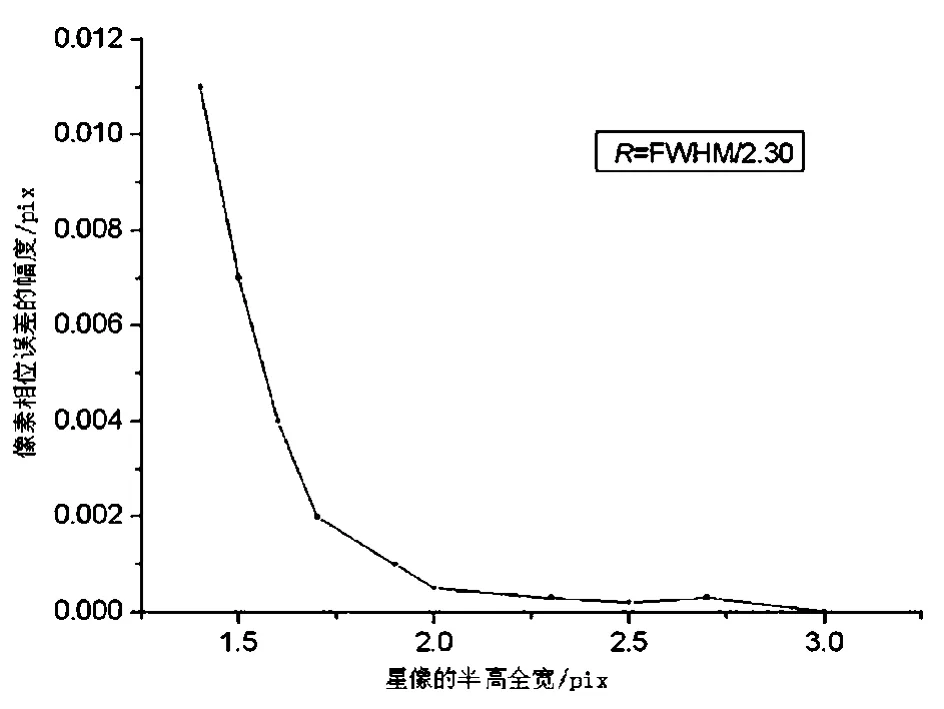
图11 横轴是星像的半高全宽,纵轴是像素相位误差的幅度Fig.11 Amplitude of pixel-phase error variation versus true FWHM
5 像素相位误差对位置测量精度的影响
生成的星像的半高全宽为1.4~2.2,且两相邻值间距为0.1的一系列仿真图像,其中每幅图像添加位置和通量都随机的星(更符合实际图像的特征)。同样采用高斯拟合法,并在实验过程中分3种情况(R参与迭代,R不参与迭代且大小为FWHM /,R不参与迭代且大小为FWHM/2.30)进行实验,比较这3种方法在不同半高全宽下的位置测量精度。先采用李展[8]等人的方法归算出每一颗星像位置的标准差,为了方便,进一步用所有星像位置的平均标准差来反映算法的精度。图12表示这3种方法拟合星像的位置精度。其中横轴为星像的半高全宽,左图和右图的纵轴分别代表x,y方向拟合星像位置的平均标准差大小,显然平均标准差越小,精度越高。
实验发现:(1)R不参与迭代其大小取FWHM/2.30时,高斯模型的半高全宽和星像真实的半高全宽偏得较大,此时高斯模型是不精确的。在半高全宽小于2 pix时会受像素相位误差的影响而导致此方法的位置测量精度不高。(2)R不参与迭代其大小取FWHM /时,高斯模型的半高全宽等于星像真实的半高全宽,此时认为高斯模型等价于ePSF模型(式4),这种情况没有像素相位误差。此时R参与迭代的高斯模型与ePSF模型都是精确的拟合模型,它们在各半高全宽下精度近似相等。(3)随着半高全宽的增大,像素相位误差的影响程度越来越小,在星像的半高全宽大于2 pix时,3种方法的精度近似相等(图12)。
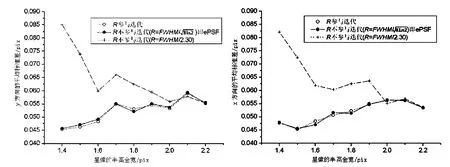
图12 (a)x方向的平均标准差大小 (b)y方向的平均标准差大小Fig.12 (a)Standard deviations of x positions versus true FWHM (b)Standard deviations of y positions versus true FWHM
6 结论
为了深入探究像素相位误差的规律,生成一系列仿真图像并采用二维高斯函数模型作为点扩散函数模型。实验表明:(1)拟合模型的半高全宽与星像真实的半高全宽偏差越大,像素相位误差的幅度越大,反之亦真。(2)当星像真实的半高全宽大于2 pix时,像素相位误差可以忽略不计。(3)当高斯模型的半高全宽参与迭代拟合时,高斯与ePSF这两个函数模型拟合的位置精度近似相等。
致谢:感谢暨南大学计算机系孟小华、李展老师在实验中提出的建设性意见和提供的帮助。
[1]Stone R C.A Comparison of Digital Centering Algorithms[J].AJ,1989(97):1227 - 1237.
[2]Zacharias N,Urban S E,Zacharias M I,et al.The First Us Naval Observatory CCD Astrograph Catalog(UCAC1) [J].AJ,2000,120(4):2131 - 2147.
[3]Zacharias N,Urban S E,Zacharias M I,et al.The Second Us Naval Observatory CCD Astrograph Catalog(UCAC2) [J].AJ,2004,127(5):3043 - 3059.
[4]Zacharias N,Finch C,Girard T,et al.The Third US Naval Observatory CCD Astrograph Catalog(UCAC3) [J].AJ,2010,139(6):2184 - 2199.
[5]Zacharias N.UCAC3 Pixel Processing [J].AJ,2010,139(6):2208 - 2217.
[6]Anderson J,King I R.Toward High Precision Astrometry with WFPC2.I.Deriving an Accurate Point-Spread Function [J].The Publications of the Astronomical Society of the Pacific,2000,112(776):1360-1392.
[7]CFITSIO [EB/OL].http://heasarc.gsfc.nasa.gov/.
[8]李展,彭青玉,韩国强.CCD图像数字定心算法的比较 [J].天文学报,2009,50(3):340-348.Li Zhan,Peng Qingyu,Han Guoqiang.Comparison of Digital Centering Algorithms Based on CCD Images[J].Acta Astronomica Sinica,2009,50(3):340 - 348.
