CA-Markov模型在舟山市土地利用中的应用研究

陈敏纳,徐林洁,陶 蓉,缪 芳,林顺风,马新生

(浙江外国语学院理工学院,浙江杭州310012)

0 引 言

城市土地的可持续利用是社会可持续发展的基础.开展土地利用的计算机模拟研究,不仅减少了实验资金和时间的大量投入,而且为制定科学、有效的土地利用管理策略提供支持和借鉴,为区域社会经济可持续发展提供指导.根据复杂适应系统理论知,土地利用系统是一个复杂动态反馈系统,而元胞自动机具有利用简单的、局部规则的和离散的方法,描述复杂的、全局的、连续系统的能力.因此,在Markov模型的基础上,结合CA模型(元胞自动机),构建CA-Markov复合模型,对复杂适应性系统进行模拟具有良好理论和实际意义[1,2].

关于CA-Markov模型(Cellular Automaton-Markov模型)在土地利用中的应用在国内外已有较多研究[1-5],这些方法主要是通过CA-Markov模型模拟方法和景观生态学相结合进行定量分析,利用GIS空间统计功能和Arc View软件的扩展模块Patch Analyst[5],研究区域的景观格局变化,但计算量较大,且计算方法复杂.为此,刘县明[6]18首次引入了从众系数的概念,给出了一种简单且易于使用的CAMarkov复合模型,并给出了实际应用实例,但文中没有讨论复合模型中转移概率与从众系数之间的关系.

本文以文献[6]中的CA-Markov复合模型为基础,给出了概率转移矩阵与从众系数矩阵的关系,完善了CA-Markov复合模型的理论基础.然后以舟山市国土资源局提供的舟山市土地变更统计数据为例,构建了基于从众系数矩阵的CA-Markov模型,提出了一种更为简便的CA-Markov复合模型计算新方法,并得到相应的土地利用变化规律,为城市土地管理部门合理配置土地资源提供决策依据.建立本文的模型时,用地演化参数主要是通过对一个已知历史时段的用地情况来确定的,且假定城市发展具有连续性和均衡性.

1 CA-Markov复合模型的构建

应用CA-Markov模型对实际的复杂自适应系统进行模拟时,关键的是从众系数矩阵的确定[6]20.

1.1 从众系数及从众系数矩阵

考虑到每个元胞既有从众性又有保持自我状态的特性,我们引入从众系数和从众系数矩阵的概念.

定义1[6]18设元胞空间L={cij|1≤i≤n,1≤j≤n},某一状态类型为k的元胞cij转变为其邻居元胞中占多数的状态类型l,所要求的l状态类型元胞的最少个数称为从众系数,记为vkl.

定义2 称由从众系数构成的矩阵为从众系数矩阵.记为

为方便研究,本文作以下规定:

(1)CA模型均采用常用的Moore型邻居;(2)模型边界元胞的邻居用周期循环得到;(3)元胞的总个数为n×n=N=50×50;(4)元胞的状态设置为S=6种.

由从众系数的定义知,从众系数vkl具有以下性质[6]19.

性质1 当元胞cij的邻居元胞占多数状态类型的元胞个数大于或者等于从众系数vkl时,cij的状态类型改变;反之,状态类型保持不变.

性质2 从众系数矩阵的对角线元素的值可统一设置为零.

性质3 从众系数vkl的取值范围为:{2,3,4,5,6,7,8}.

性质4 从众系数vkl值越小,则元胞由状态类型k转化为状态类型l的概率越大;反之,概率越小.

1.2 CA-Markov模型演化规则

设当前元胞cij记为c0,8个邻居元胞,分别记为c1,...,c8,如图1所示.

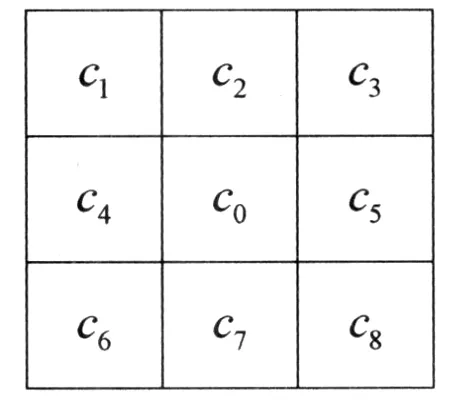
图1 Moore型邻居

定义CA-Markov模型的演化规则如下:

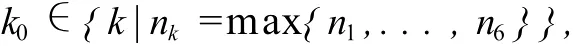
若有多个,则随机选取一个.

(3)若max{n1,...,n6}≥vl0k0(l0表示当前元胞cij的状态类型),则cij=k0.

1.3 CA-Markov模型从众系数矩阵的确定

在Markov模型中,转移概率pkl表示状态类型k转化到状态类型l的概率大小,这和从众系数的意义相近,所以不妨考虑由转移概率矩阵来得到从众系数矩阵.设Markov模型中的转移概率矩阵为

记pik1,pik2,...,pikS为转移概率矩阵第i行的一个从小到大的排列,则相应得到从众系数矩阵的第i行

这样得到的从众系数矩阵,继承了Markov模型中转移概率矩阵的特性.由两者的对应关系,容易证明以下两个性质.

性质1 转移概率越大,从众系数越小;反之,从众系数越大.

性质2 从众系数越小,对应土地类型的元胞个数增加越快.

2 CA-Markov模型在舟山市土地利用中的应用

2.1 舟山概况

舟山市位于浙江省东北部,背靠沪杭甬,面向太平洋,地理坐标北纬29°32′至31°04′,东经121°30′至123°25′,踞我国沿海南北航线与长江“黄金水道”交汇的咽喉要道,舟山市是我国唯一的以群岛组成的省辖地级市.截止2009年底,总人口96.77万人,人口密度672人/km2[7].近年来,随着世界经济向沿海地区集中,舟山岛逐渐成为重要的经济发展载体.

根据2007年土地变更调查数据,舟山市土地总面积1402km2,人均土地面积2.17亩,远低于同期浙江省3.35亩/人,全国11.65亩/人,土地资源十分紧缺.土地结构也发生了较大变化,主要表现为耕地面积在不断减少和非农建设用地在逐步增加.

2.2 概率转移矩阵与从众系数矩阵的确定

经查阅舟山市土地变更统计表[8],得到2007年末舟山市土地利用各类型的比例、2006年末到2008年末的土地利用转移矩阵,见表1和表2.

表1 2007年末舟山市土地利用各类型的比例

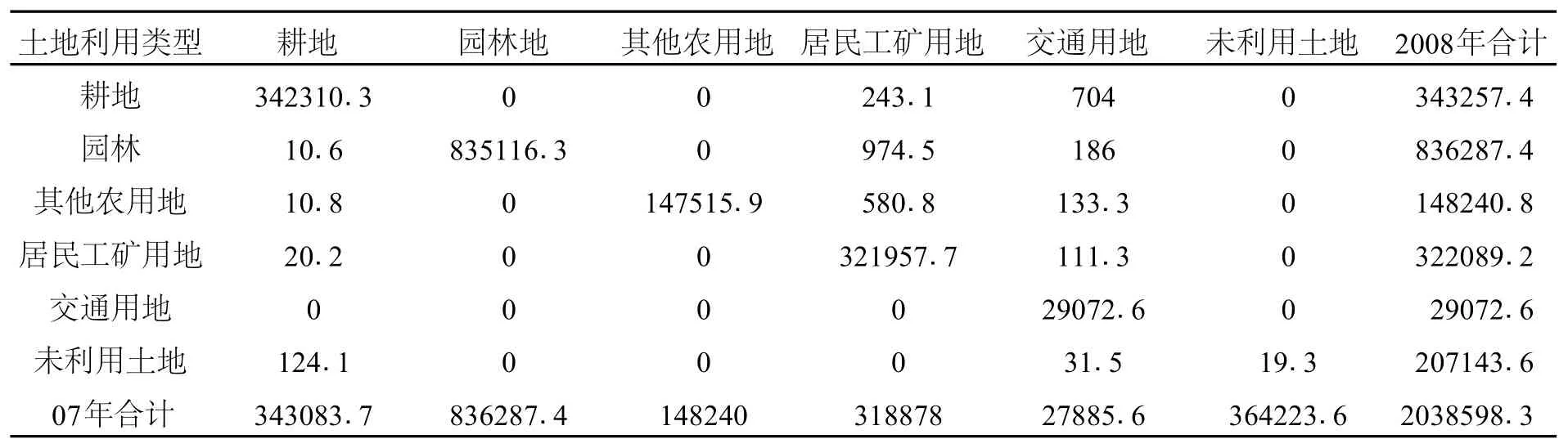
表2 舟山市2006年末到2008年末土地利用转移矩阵(单位:hm2)

根据土地利用转移矩阵,结合实际情况,确定其土地概率转移矩阵,见表3.

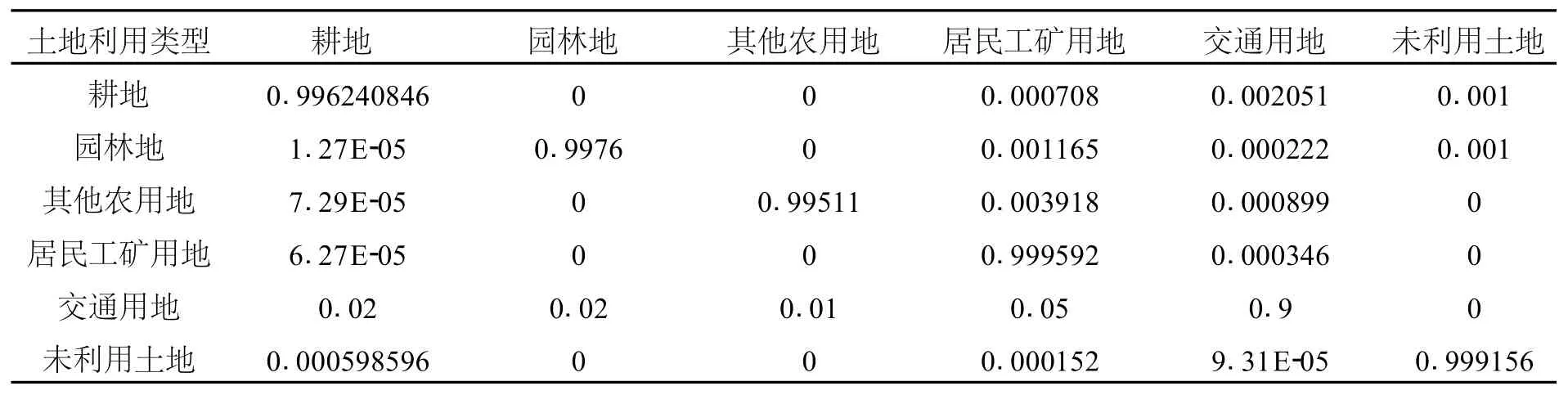
表3 舟山市土地概率转移矩阵

根据CA-Markov模型的确定方法,得到如下从众系数矩阵.

2.3 CA-Markov模型的预测结果及分析

根据前述演化规则,利用Matlab软件模拟计算,得到演化结果如图2～4所示.

对以上演化结果进行分析可得:

(1)由图2和图3可知,舟山市土地类型的面积将发生较大变化.耕地、园林地、其他农用地、交通用地、未利用土地都有所减少;而居民工矿用地将迅速扩展,从初始的16.24%最终增加到62.36%,是变化最为明显的.

(2)从各状态类型的元胞变化率来看,居民工矿用地和园林地的变化幅度较大,其他土地类型变化不显著,但经过一段时间后,变化率都向零靠近.各用地类型元胞数震荡增加或减少,呈现出非线性性,说明了CA-Markov模型具有模拟复杂适应系统的能力,同时也表现出了土地利用系统非线性的复杂特征.

(3)CA-Markov复合模型不仅具有空间演化的优势,还具有Markov过程的优良性质,比简单的Markov模型和CA模型更优越.

3 结论与建议

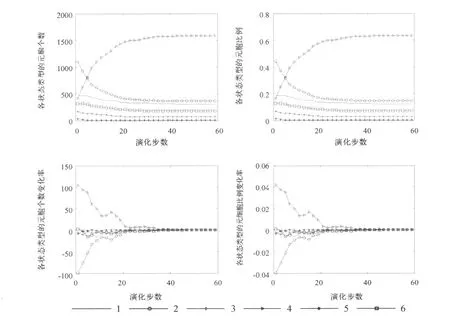
图4 各状态类型元胞个数、比例及变化率随步数的关系图

(1)舟山市土地类型的面积将发生较大变化.居民工矿用地的扩张,占用大量耕地和园林地已成为该市土地结构变化的突出问题.需要加强耕地和园林地的保护.建议提高建设用地整体集约利用程度,在保证生态环境不被破坏的前提下,适度进行滩涂围垦和围海造地,缓解建设用地紧缺的局面.

(2)CA模型具有模拟复杂系统空间变化的能力,Markov模型具有进行长期预测的优势,将二者有机地结合在一起构建的CA-Markov模型,能够反映区域土地利用变化的复杂性和随机性,能更加深刻、直观地揭示土地变化的过程.

本文的模型中,用地演化参数主要是通过对一个已知历史时段用地情况来确定的,且预先假定了城市发展的连续性和均衡性,但纵观世界城市发展历史,城市演变的速度往往是不均衡的.因此城市不同时段在发展速度的差异性有待进一步研究.

[1]Almeida CM D,BattyM,Monteiro,AM V,et al.Stochastic cellular automatamodeling of urban land use dynamics:empirical development and est imation[J].Computers,Environment and Urban Systems,2003,27(5):481-509.

[2]熊利亚,常斌,周相广.基于地理元胞自动机的土地利用变化研究[J].资源科学,2005,27(4):38-43.

[3]侯西勇,常斌,于信芳.基于CA-Markov的河西走廊土地利用变化研究[J].农业工程学报,2004,20(5):286-291.

[4]汤洁,汪雪格,李昭阳,等.基于CA-Markov模型的吉林省西部土地利用景观格局变化趋势预测[J].吉林大学学报,2010,40(2):406-411.

[5]杨国清,刘耀林,吴志峰.基于CA-Markov模型的土地利用格局变化研究[J].武汉大学学报,2007,32(5):414-418.

[6]刘县明.CA-Markov模型及其在城市土地中的应用研究[D].南昌:南昌大学,2007.

[7]张荣,孔海英.2009舟山年鉴[M].北京:中国统计出版社,2009:1-10.

[8]舟山市2008年土地变更调查统计[EB/OL].(2009-11-27).http://www.zsblr.gov.cn/mlx/jhtj/zdxm/zdxm-3042.h tml.