固定瓦－可倾瓦组合径向轴承－柔性转子系统非线性运动分析

吕延军，张永芳，于杨冰，虞 烈

(1.西安理工大学 机械与精密仪器工程学院，西安 710048;2.重庆大学 机械传动国家重点实验室，重庆 400030;3.西安理工大学 印刷包装工程学院，西安 710048;4.西安交通大学 机械电子及信息系统研究所，西安 710049)

固定瓦－可倾瓦组合径向轴承－柔性转子系统非线性运动分析

吕延军1，2，张永芳3，于杨冰1，虞 烈4

(1.西安理工大学 机械与精密仪器工程学院，西安 710048;2.重庆大学 机械传动国家重点实验室，重庆 400030;3.西安理工大学 印刷包装工程学院，西安 710048;4.西安交通大学 机械电子及信息系统研究所，西安 710049)

针对流体润滑中具有Reynolds边界条件的非定常Reynolds方程，运用Castelli法求解Reynolds方程，生成了单块轴瓦坐标系下的非线性油膜力数据库。根据固定瓦－可倾瓦组合滑动轴承的结构特点，对单瓦库进行检索、插值和拼装，获得了固定瓦－可倾瓦组合径向滑动轴承的非线性油膜力。针对柔性转子－组合滑动轴承系统，运用自适应步长Runge－Kutta法和Poincaré映射计算了不同支点比下的轴颈的非线性运动轨迹。数值结果表明，转子系统表现出周期解，倍周期解和准周期解等非线性现象，支点比为0.6时的系统性能略优于支点比为0.5时的系统性能。

固定瓦－可倾瓦组合径向轴承;非线性;动力学;分岔

目前，围绕轴承－转子系统的非线性动力学行为及稳定性的研究，国内外学者先后做了大量的工作［1－3］，但是大多数学者研究的轴承形式相对简单。文献［4－7］采用固定瓦轴承(如圆轴承、椭圆轴承、油叶型轴承)来进行非线性油膜力的计算。文献［8，9］在分析可倾瓦轴承的动力特性及其稳定性时，只做了线性稳定性分析。文献［10］提出了一种可倾瓦轴承的完整动力分析模型及其动力特性系数的组装技术。文献［3，11］在求解可倾瓦轴承的压力分布时，沿轴瓦轴向方向对油膜压力分布采用了抛物线假设，文献［11］用近似解析的方法分析了可倾瓦轴承－转子系统响应的同步周期运动及其稳定性。文献［12，13］进行了固定瓦轴承非线性油膜力数据库方法的研究，为高效地计算非线性油膜力开辟了新途径。文献［14］运用数据库方法求解了三瓦可倾瓦轴承的非线性油膜力，并对可倾瓦轴承－Jeffcott转子系统的不平衡响应进行了分析。

本文基于动态Reynolds方程和Reynolds破膜条件，建立了单块轴瓦的非线性油膜力数据库，根据固定瓦－可倾瓦组合滑动轴承的结构特点，配以快速检索和精确插值方法，通过组装技术获得了固定瓦－可倾瓦组合径向滑动轴承的非线性油膜力。在很大程度上免除了系统非线性分析中的大量的繁琐的重复计算工作，大大减少了计算工作量，提高了计算效率。此外，运用Poincaré映射和Runge-Kutta法分析了固定瓦－可倾瓦组合径向滑动轴承支承的对称柔性转子系统的不平衡响应。对比了组合轴承－Jeffcott柔性转子非线性系统在不同支点比下的涡动轨迹，分析了支点比对系统性能的影响。数据结果展现了组合轴承－柔性转子系统的周期解，倍周期解和准周期解等丰富的非线性现象。

1 系统方程

图1所示的固定瓦－可倾瓦组合径向轴承－对称柔性Jeffcott转子系统，其动力学方程可写为:

式中:M和K分别为转子的质量和刚度矩阵，f是固定瓦－可倾瓦组合轴承非线性油膜力向量，Q是施加在转子上的周期激励力向量，X是转子的位移向量。其表达式分别为:

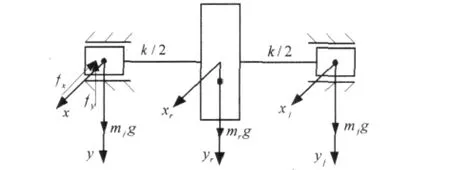
图1 对称柔性Jeffcott转子系统示意图Fig.1 Schematic of symmetrical flexible rotor system

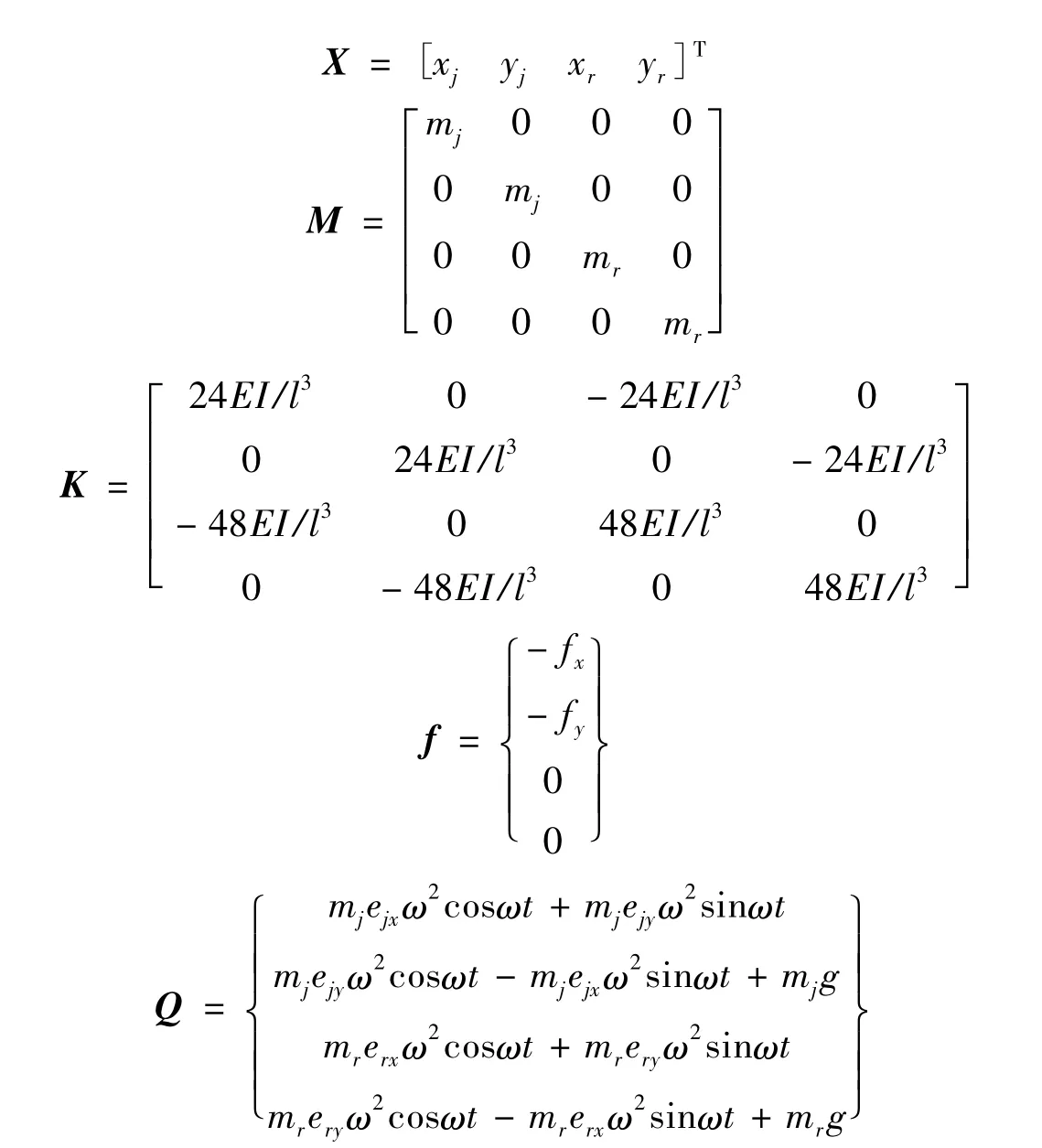
其中2mj和mr分别为集总到2个轴颈及圆盘处的质量，且2mj+mr=2m(转子总质量);E，I分别为转子的弹性模量及转子截面的赤道惯性矩，l是两个轴承的中心距;2fx和2fy分别是2个轴承处在x和y负方向的非线性油膜力分量;g是重力加速度，emn(m=j，r;n=x，y)是轴承及圆盘处不平衡质量偏心距在x和y方向的分量。

2 固定瓦－可倾瓦组合滑动轴承非线性油膜力

图2所示为固定瓦－可倾瓦组合轴承结构示意图。图中，XObY为轴承坐标系; ξiOiηi为第 i块轴瓦的单瓦坐标系;下标i为顺转动方向的瓦块编号;Oj为轴颈中心;Ob为轴承中心;O*

i为第i块轴瓦几何中心的初始位置，Oi为第i块轴瓦的瓦弧中心;R为瓦弧半径(无量纲);αi为第i块轴瓦绕支点的摆角(rad);φki为第i块轴瓦的支点位置角(rad)，是从轴承下方垂线顺转动方向到瓦支点的角度;m为预负荷(无量纲);ε为轴颈中心在轴承坐标系中的偏心距(无量纲);εi为轴颈中心在第i块轴瓦坐标系中的偏心距(无量纲);为轴颈的转速(无量纲);θ为轴颈中心在轴承坐标系中的偏位角(rad);φ为由轴承上方垂线开始计量的角度(rad);φi为从连心线OjOi开始计量的角度(rad);W为轴承的无量纲载荷。

图2 固定瓦－可倾瓦组合轴承结构示意图Fig.2 Schematic of fixed-tilting pad combination journal bearing

对于组合轴承中的固定瓦块，由于它不能动，油膜厚度仅由偏心率、偏位角、预负荷等固定瓦参数决定，因而可将其视为剖分式圆轴承的上瓦，固定瓦的非线性油膜力的获得方法可参考文献［12］，下面介绍可倾瓦非线性油膜力的获得方法。

非线性油膜力数据库方法的关键在于确定动态Reynolds方程中扰动项的数值范围，第i块瓦润滑的无量纲动态Reynolds方程在第i块瓦的坐标系中可表示为:

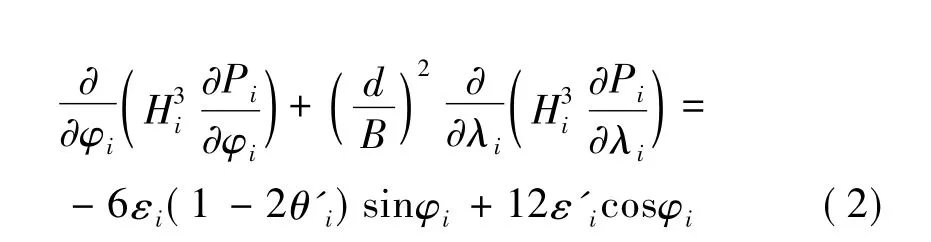
式中:Hi为第i块瓦坐标系中的无量纲油膜厚度，Pi为第i块瓦坐标系中的无量纲油膜压力函数，φi为第i块瓦坐标系中从OjOi的连线到油膜位置的角度(rad)(如图2所示)，λi为第i块瓦坐标系中的无量纲轴向坐标，d/B为轴承宽径比的倒数，εiθ'i为转子轴颈中心在切向方向上的无量纲扰动速度，ε'i为转子轴颈中心在径向方向上的无量纲扰动速度。

(3) 当 εi(1－2θ'i)=0，ε'i=0 时，无量纲切向和径向油膜力 Fθ=0.0，Fε=0.0。

通过对动态Reynolds方程的处理，采用Castelli法求解动态Reynolds差分方程，设油流态为层流，边界条件采用具有油膜破裂边(油膜区域出现气穴，油膜完备区和破裂区的交界线即是油膜破裂边)的Reynolds边界条件:

其中 φi1是油膜起始边的角度;φip是油膜破裂边的角度。

以单块轴瓦为基础，由三个变量:偏心率 εi=(0，0.95)，瓦起始角 φi1=(0°，360°)，挤压比 Qi=( －1，1)(Qi包含和)，建立在各种长径比和瓦张角下的单瓦非线性油膜力数据库。

第i块轴瓦坐标系中的可倾瓦膜厚表达式为:

式中:c是轴承半径间隙;ei为轴颈中心在第i块轴瓦坐标系中的偏心距。定义无量纲参数:Hi=hi/c，εi=ei/c，则无量纲油膜厚度表达式为:

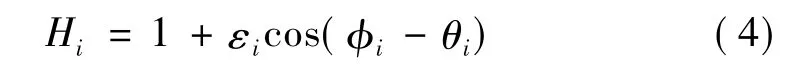
式中:φi是第i块瓦坐标系中从ηi轴负向开始计量的角度，θi是轴颈中心在第i块瓦坐标系中偏位角(如图3所示)。

图3 可倾瓦单瓦坐标系示意图Fig.3 Schematic of single pad of tilting-pads coordinate system

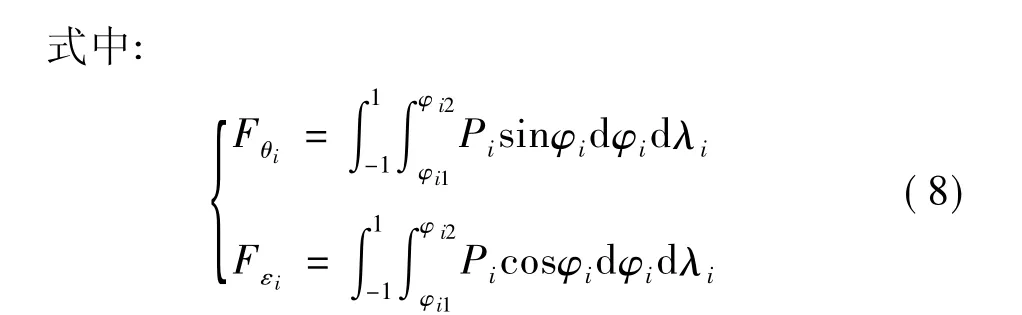
在第i块轴瓦坐标系中，相对摆角αi/Ψ的迭代计算采用以下形式实现:

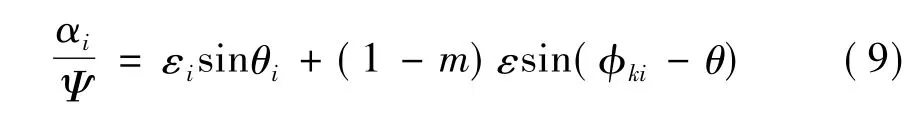
通过编制计算机程序来计算固定瓦－可倾瓦组合径向滑动轴承的非线性油膜力(见图2)及其转子系统的不平衡响应。轴瓦摆动的计算是一个迭代过程，其相对摆角αi/Ψ具体迭代过程如下:

① 给定已知量如预负荷m，偏心率ε，偏位角θ，支点位置角φki，设定相对摆角的初值(αi/Ψ)0;

② 设定单块瓦在第i块轴瓦坐标系中的起始位置角φi1;

③ 将m，ε，θ，φki，φki－θ，αi/Ψ 代入式(5)求出相对偏心率εi;

④ 由式(7)求解相对偏位角θi;⑤ 由式(9)求得相对摆角αi/Ψ;

⑥ 根据相对摆角的收敛准则(见式10)，可以判别轴瓦是否平衡。若式(10)未满足，则修正相对摆角，重复③－⑥步;若式(10)已满足，则继续下一块轴瓦αi+1/Ψ 的计算。

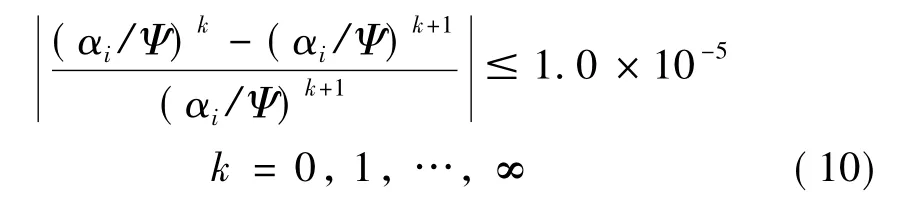
利用相似关系，调用单块瓦非线性油膜力数据库，即可求得所有轴瓦在其自身坐标系中的无量纲非线性油膜力Fξi和Fηi，将他们转化为轴承坐标系中的无量纲油膜力FXi和FYi:

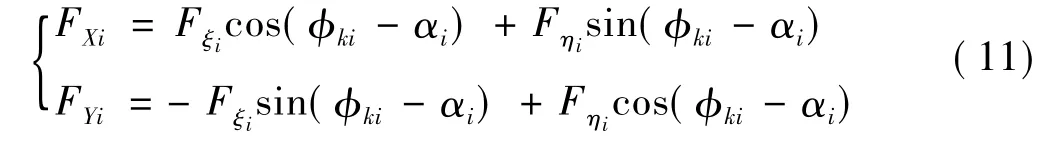
最后组装固定瓦－可倾瓦组合轴承的油膜力即可获得轴承坐标系中的总的非线性油膜力FX和FY:

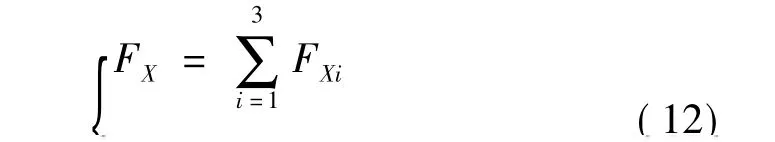
3 数据库方法的验证

文献［15］的附录中给出了常用滑动轴承的特性数值表，计算时假设在层流工况下，未考虑粘度不均匀分布和进油压力的影响。运用数据库方法求解得到的非线性油膜力与文献［15］中的结果进行对比，验证数据库方法及其计算程序的正确性。

以图4中的两轴向槽圆轴承为计算对象，取长径比B/d=0.8，瓦张角 β =150°，计算该轴承的无量纲承载力，并和参考文献［15］附录中表B－5给出的计算结果进行了对比，其计算结果如图5所示。

图5描述了两种计算方法的吻合度。针对相同的计算对象，基于数据库计算得到的结果和参考文献［15］中给出的结果取得了很好的一致，表明数据库方法及其计算程序的正确性。

图4 两轴向槽圆轴承结构简图Fig.4 Schematic of cylindrical bearing with two axial grooves

4 数值算例与结果

图1所示的对称柔性Jeffcott转子系统，选用图2所示的固定瓦－可倾瓦组合滑动轴承支承。固定瓦块取剖分式圆轴承的上半瓦，其几何参数为:宽径比B/d=0.8，瓦张角β1=180°。可倾瓦取两块左右对称分布的可倾瓦，其几何参数为:宽径比B/d=0.8，瓦张角βi=80°，支点比为～βi/βi=0.5，支点位置角分别为φk2=315°，φk3=45°，预负荷 m=0.5，间隙比 Ψ =0.003，动力润滑粘度μ=0.03 Pa·s。对称柔性转子的直径d=0.558 m，转子长度 l=1.6 m，圆盘直径 dr=1.12 m，圆盘宽度0.2 m，质量密度ρ=7 800 kg/m3，弹性模量E=2×1011N/m2。作用在圆盘处集中质量的质量偏心在y方向上取0.000 1 m(例如 erx=0.0，ery=0.000 1)。作用在轴颈处集中质量的质量偏心在x和y方向上均取0.0(例如 ejx=0.0，ejy=0.0)。

在中心支点(支点比为～βi/βi=0.5)的情况下，当转子转速低于4 000 r/min时，转子的不平衡响应是稳定的周期运动。图6所示为转速为n=4 000 r/min时，轴颈中心和圆盘中心的周期运动轨迹。随着转子转速增加，当n=4 950 r/min时，周期2分岔发生，轴颈中心的运动轨迹如图7所示，此时轴颈中心的运动是半频涡动。随着转子转速的进一步增加，系统的响应出现了复杂的准周期运动，图8(a)中给出了转速n=6 000 r/min时，轴颈中心的准周期运动轨迹，图8(b)示出了转速n=6 000 r/min时，相应的轴颈中心的环形吸引子，即 Poincaré映射在 X－Y坐标平面上的投影，图8(c)示出了相应的Y方向频谱图。

图8 n=6 000 r/min时，轴颈中心的准周期分岔Fig.8 The quasi-periodic bifurcation of the center of the journal for n=6 000 r/min

在偏支点(支点比为～βi/βi=0.6)的情况下，当转子转速低于5 000 r/min时，转子的不平衡响应是稳定的周期运动。图9所示为转速n=5 000 r/min时，轴颈中心和圆盘中心的周期运动轨迹。随着转子转速增加，周期2分岔发生，此时轴颈中心的运动是半频涡动，当n=6 000 r/min时，轴颈中心的运动轨迹如图10所示。随着转子转速的进一步增加，系统的响应表现为准周期运动，图11(a)中给出了转速n=9 000 r/min时，转子中心的准周期运动轨迹，图11(b)示出了转速n=9 000 r/min时，相应的转子中心的环形吸引子，即Poincaré映射在X－Y坐标平面上的投影，图11(c)示出了转速n=9 000 r/min时，相应于准周期轨迹Y方向的频谱图。

图12给出了n=4 000 r/min时，不同支点比下，轴承处和圆盘处的轴心运动轨迹。图12(a)和图12(b)分别示出了支点比为0.5和0.6时，轴承及圆盘处轴心的运动轨迹。

图11 n=9 000 r/min时，轴颈中心的准周期分岔Fig.11 The quasi－ periodic bifurcation of the center of the journal for n=9 000 r/min

图12 n=4 000 r/min时，不同支点比下的轴承处和圆盘处的轴心运动轨迹Fig.12 The periodic orbit of the journal center and the disk center when the pivot ratios are 0.5 or 0.6 respectively as the rotor speed n=4 000 r/min

5 结论

基于数据库方法，计算了固定瓦－可倾瓦组合轴承的非线性油膜力。运用自适应步长Runge-Kutta法和Poincaré映射得到了轴颈中心的轨迹图和Poincaré映射图，研究了固定瓦－可倾瓦组合滑动轴承支承的对称柔性Jeffcott转子系统的不平衡响应。系统的不平衡响应表现为:周期运动、周期－2运动、准周期运动等。同时考察了可倾瓦支点比的影响，通过数值算例可知，在相同参数的情况下，支点比为0.6时的运动轨迹振幅略小于支点比为0.5时的运动轨迹振幅，因而前者的系统性能略优于后者。数值仿真的结果对实际的固定瓦－可倾瓦组合径向滑动轴承支承的转子系统的设计提供了理论依据。

［1］Ha H C，Kim H J，Kim K W.Inlet Pressure Effects Thermohydrodynamic Performance of a Large Tilting Pad Journal Bearing［J］.ASME Journal of Tribology，1995，117(1):160－165.

［2］Ha H C，Yang S H.Excitation Frequency Effects on the Stiffness and Damping Coefficients of a Five-Pad Tilting Pad Journal Bearing［J］.Journal of Tribology，1999，121(3):517－522.

［3］ Abu-Mahfouz I，Adams M L.Numerical Study of Some Nonlinear Dynamic of a Rotor Supported on a Three-pad Tilting Pad Journal Bearing(TPJB)［J］.ASME Journal of Vibration and Acoustics，2005，127(3):262 －272.

［4］ Lu Y J，Zhang Y F，et al.Non-linear Analysis of a Flexible Rotor System with Multi-Span Bearing Supports［J］.Journal of Engineering Tribology，2008，222(3):87 －95.

［5］ Lu Y J，Liu H，Dai R，et al.A method for determining the periodic solution and its stability of nonlinear bearing-rotor system based on observed states of the system［J］.Journal of Engineering Tribology，2009，223(2):137－149.

［6］ Lu Y J，Dai R，Hei D，et al.Stability and bifurcation of a non-linear bearing-flexible rotor coupling dynamic system［J］.Journal of Mechanical Engineering Science，2009，223(4):835－849.

［7］沈光琰，肖忠会，郑铁生，等.油叶型轴承—不平衡转子系统的非线性动力学分析［J］.航空动力学报，2004，19(5):604－609.

［8］李小江，朱 均.300 MW汽轮发电机组径向可倾瓦轴承性能研究［J］.润滑与密封，1996，113(1):29－32.

［9］乔 广，王丽萍，郑铁生.可倾瓦滑动轴承系统线性稳定性分析［J］.工程力学，2007，24(11):180－185.

［10］王丽萍，乔 广，郑铁生.可倾瓦轴承的完整动力分析模型及计算方法［J］.机械工程学报，2008，44(1):75－80.

［11］ Brancati R，Rocca E，Russo R.Non-linear stability analysis of a rigid rotor on tilting pad journal bearings［J］.Tribology International，1996，29(7):571 －578.

［12］王 文，张直明.油叶型轴承非线性油膜力数据库［J］.上海工业大学学报，1993，14(4):299－305.

［13］孟志强，徐 华，朱 均.基于Poincaré变换的滑动轴承非线性油膜力数据库方法［J］.摩擦学学报，2001，21(5):223－227.

［14］焦映厚，陈照波，等.Jeffcott转子－可倾瓦滑动轴承系统不平衡响应的非线性分析［J］.中国电机工程学报，2004，24(12):227－232.

［15］张直明，张言羊，谢友柏，等.滑动轴承的流体动力润滑理论［M］.北京:高等教育出版社，1986.

Nonlinear dynamic analysis of a flexible rotor system with combined fixed-tilting pad journal bearings

LÜ Yan-jun1，2，ZHANG Yong-fang3，YU Yang-bing1，YU Lie4

(1.School of Mechanical and Instrumental Engineering，Xi’an University of Technology，Xi’an 710048，China;2.State Key Laboratory of Mechanical Transmission，Chongqing University，Chongqing 400030，China;3.School of Printing and Packaging Engineering，Xi’an University of Technology，Xi’an 710048，China;4.Institute of Mechatronics and Information Systems，Xi’an Jiaotong University，Xi’an 710049，China)

Based on Reynolds equation with Reynolds boundary conditions，Castelli method was employed to solve Reynolds equation for oil lubrication in bearings.By doing so，a profile of nonlinear oil film force of single pad journal bearing was established.According to the structure of a combined journal bearing，its nonlinear oil film force was obtained using retrieval，interpolation，and assembly techniques.For a symmetrical flexible Jeffcott rotor system supported by combined journal bearings，the nonlinear motions of the rotor center were calculated using self-adaptive Runge-Kutta method and Poincar mapping with different rotational speeds and different pivot ratios.Numerical results showed that the system performance is slightly better when the pivot ratio changes from 0.5 to 0.6，and reveals nonlinear phenomena of periodic，period-doubling，quasi-periodic motion，etc.

fixed-tilting pad journal bearing;nonlinear;dynamics;bifurcation

TH113.1

A

国家重点基础研究发展计划“973”(2007CB707706);国家自然科学基金(51075327);国家重点实验室开放课题(SKLMT－KFKT－201011);陕西省自然科学基金 (2009JQ7006，2007E203);陕西省教育厅科学研究计划(09JK680，075K340)

2009－12－17 修改稿收到日期:2010－03－31

吕延军 男，博士，教授，1972年生