大型非线性转子-密封-轴承系统的不平衡响应与稳定性
2011-01-25刘占生叶建槐
崔 颖,刘占生,叶建槐
(哈尔滨工业大学 能源科学与工程学院,哈尔滨 150001)
大型非线性转子-密封-轴承系统的不平衡响应与稳定性
崔 颖,刘占生,叶建槐
(哈尔滨工业大学 能源科学与工程学院,哈尔滨 150001)
对实际大型汽轮机转子-密封-轴承系统建立了具有超大规模维数的非线性动力学模型,该模型考虑了密封的非线性激振力、可倾瓦轴承的弹性支承力、转子的阻尼力、不平衡质量力和重力。采用Newmark方法对其进行数值求解,模拟出转子升速过程中汽流激振现象的典型特征和发生汽流激振的失稳转速,并且得到系统参数对转子不平衡响应和稳定性的影响规律。结果表明:适当的增大转子的阻尼、密封的半径间隙和密封流体轴向流速可提高转子发生汽流激振的失稳转速,这为在设计和运行中提高实际大型汽轮机转子-密封-轴承系统的稳定性提供了参考依据。
转子-密封-轴承系统;非线性;高维;不平衡响应;失稳转速
当前我国电站汽轮发电机组正向着大容量、超临界和超超临界机组发展。汽轮机蒸汽参数的提高导致高中压缸进汽密度增大、密封前后压差提高,致使作用在高中压转子的密封激振力增强,容易诱发高中压转子失稳,产生很大的具有低频特性的汽流激振故障。由于密封流体激振力近似的正比于机组的出力,因而汽流激振引起的不稳定振动已成为限制超临界和超超临界机组出力和安全稳定运行的重要因素[1]。
在转子-密封-轴承系统动力学特性分析中建立准确的密封力模型是研究的基础。Thomas[2]提出了线性化的八参数模型,在一定程度上解释了某些物理现象;Black[3]在Thomas模型基础上考虑了流体的惯性效应。Childs和 Yule等[4,5]提供了一种基于控制体的等效动特性模型来求解密封流体动力特性的方法,这些模型均属于线性模型的范畴,在描述转子大涡动状态下密封力的非线性特征时具有很大的局限性。Muszynska和 Bently[6]在大量实验研究的基础上提出了Muszynska模型。该模型认为密封流体激振力的旋转效应是诱发转子失稳的主要因素,并较好地反映了密封力的非线性特征,具有明确的物理意义和简洁的解析表达式,方便于计算和分析,迄今得到了较多的应用。文献[7-11]采用Muszynska模型对单盘转子-密封系统非线性动力特性进行了理论分析,揭示出具有较少自由度模型转子的分岔与混沌等复杂的非线性动力学行为,得到了关于转子稳定性的一些结论,对于转子-密封系统的设计具有一定的指导意义。实际大型汽轮机转子-密封-轴承系统具有超大规模的自由度,非线性动力学分析难度很大。本文建立了某型超超临界汽轮机高中压转子-密封-轴承系统的高维非线性动力学模型,采用Newmark法对其进行数值分析,计算结果很好地模拟出该转子在升速过程中发生汽流激振的失稳转速及汽流激振的典型振动特征,并且对系统参数影响转子动力响应和稳定性的规律进行了探讨。
1 大型非线性转子-密封-轴承系统的建模
1.1 转子-密封-轴承系统的高维非线性动力学方程
以某型超超临界汽轮机高中压转子-密封-轴承系统为例,建立系统高维非线性动力学方程。该转子由高压和中压通流部分组成,高压部分由调节级与10级叶片构成,中压部分由7级叶片构成,转子总长8.603 m,总重量为42 026 kg。该转子系统结构的有限元模型如图1所示,转子划分为91个轴段,共92个结点,转子支承在前后两个可倾瓦滑动轴承上,高压端轴承为1#轴承,中压端轴承为2#轴承。三处密封分别位于高压末端,高、中压中间部位和中压末端。

图1 汽轮机高中压转子有限元划分模型Fig.1 Finite element model of HP-IP rotor for a steam turbine
采用Eular-Bernouli梁模型假设,利用有限元法得到该转子-密封-轴承系统具有368个自由度的高维非线性运动微分方程,如式(1)所示:

式中M为质量阵,C为阻尼阵,K为刚度阵,FB轴承油膜力,FS密封力,Q不平衡力,G重力,z广义位 移矢 量,表示为[xi,yi,- θxi,θyi]T,xi,yi和 - θxi,θyi分别为转子上第i个结点沿水平和垂直方向的位移和偏转角。
假定转子的阻尼为比例阻尼,如式(2)所示:

ω1,ω2在刚性支承下转子的第一、二阶固有频率,分别为1 948 r/min和3 438 r/min。
ξ1,ξ2分别为第一、二阶模态阻尼比。
1.2 密封激振力的模型
Muszynska密封力模型具有简洁明晰的解析表达式,对于大型轴系动态响应特性的数值计算和分析具有较好的适用性。该模型如下式所示[6];
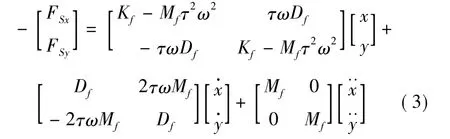
式中ω为转子的自转转速,τ为密封内流体平均周向速比,Kf、Df、Mf分别体现了流体对转子扰动运动的刚度,阻尼和惯性效应。实验和数值研究结果证实其中τ,Kf和Df均为扰动位移x,y的非线性函数,即:
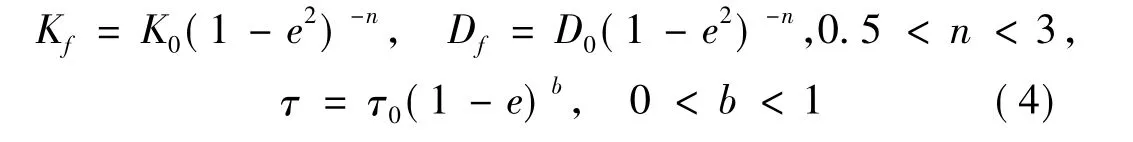
2 数值计算结果及分析
采用Newmark数值积分方法对大型汽轮机转子-密封-轴承系统的高维非线性运动微分方程进行求解,可以较为准确地计算出系统在不同的参数状态下的动力响应与稳定性。
2.1 转子不平衡响应和稳定性的数值计算和分析
转子1#、2#可倾瓦轴承的径向刚度分别1.051e9 N/m和1.124e9 N/m。Muszynska模型中密封参数的取值如表1所示。假定在转子调节级位置存在0.1mm的不平衡偏心距,选取转子两阶模态阻尼比分别为ξ1=0.08,ξ2=0.12,计算得到转子不加密封力和加密封力两种情况下1#轴承处的轴颈不平衡响应的幅频特性的对比结果。

表1 Muszynska模型中密封参数的取值Tab.1 Parameters in Muszynska model
图2所示,在不加密封力的情况下,转速1 000 r/min-8 000 r/min范围内,转子在1 960 r/min与3 660 r/min两阶临界转速附近出现振幅增大的现象;而在加密封力的情况下,转子不平衡响应振幅增大的转速分别为2 060 r/min和4 000 r/min。两种情况的对比说明:密封力的作用提高了转子的临界转速,尤其是对转子第二阶临界转速值及其响应的幅值影响较大。在密封力的作用下,转速达到7 600 r/min时转子振幅开始增大,升高转速至7 920 r/min后,因响应幅值超出密封间隙而计算被迫终止,此时转子发生碰摩。

由转子在1#轴承处轴颈振动的三维谱图(图3)所示,当转速达到7 600 r/min时转子振动开始出现低频分量,并且该低频分量的大小随着转速的升高而增大,但其频率值保持在2 060 r/min不变,该频率与转子的第一阶固有频率非常接近,可判断出此时转子发生了内共振现象,通常在工程中称这种现象为汽流激振,汽流激振的存在使转子失去动力稳定性。
2.2 转子阻尼对不平衡响应和稳定性的影响
为分析转子的阻尼对不平衡响应和稳定性的影响,在系统参数保持不变的情况下,改变转子两阶模态阻尼比的大小,计算得到1#轴承处的轴颈不平衡响应的幅频特性的变化情况。由图4可见,随着两阶模态阻尼比的增大,转子过临界转速时的振幅降低,并且转子发生汽流激振的转速也随之升高。因此可采取适当加大转子阻尼的方法来提高转子的稳定性。

图4 不同的阻尼比条件下转子的幅频特性Fig.4 Rotordynamics responses versus damping ratio
2.3 密封的半径间隙对不平衡响应和稳定性的影响
在系统参数保持不变的情况下,在0.45 mm~0.65 mm的范围内同时改变转子三处密封处半径间隙的大小,计算得到1#轴承处的轴颈不平衡响应的幅频特性的变化情况。由图5可见:随着密封半径间隙的增大,转子过临界转速时的振幅减小,并且转子发生汽流激振的转速也随之升高。因此,在保证泄漏量在允许范围内的前提下,可采取增大密封间隙的方法来提高转子的稳定性。

2.4 密封流体轴向流速对不平衡响应和稳定性的影响
在系统参数保持不变的情况下,使密封流体轴向流速在70 m/s-110 m/s之间变化,计算得到1#轴承处的轴颈不平衡响应和稳定性。由图6可见:随着密封流体轴向流速的增大,转子过临界转速时的振幅减小;并且转子发生汽流激振的转速也随之提高,因此,可利用适当加大密封流体轴向流速的方法来提高密封作用下转子的稳定性。
3 结论
(1)建立的非线性动力学模型和采用计算方法在理论上能够较好的模拟出实际大型汽轮机转子-密封-轴承系统的动力响应特性和汽流激振特性。
(2)通过对不加密封力和加密封力的转子响应分析得出:密封力使转子的临界转速有所增大,尤其对该转子的第二阶临界转速的影响较大。
(3)计算结果表明:适当的增大转子的阻尼、密封的半径间隙和密封流体轴向流速可提高转子发生汽流激振的失稳转速。这为在设计和运行中提高实际大型汽轮机转子-密封-轴承系统的稳定性提供了参考依据。
[1]史进渊,杨 宇,孙 庆,等.超超临界汽轮机技术研究的新进展[J].动力工程,2003,23(2):2252-2257.
[2]特劳佩尔.热力透平机[M].郑松宇,等译.北京:机械工业出版社,1988:603-609.
[3]Black H,Jenssen D.Effects of high-pressure ring seals on pump rotor[S].ASME paper,1971,No.71 - WA/FF -38.
[4]Childs D W,Scharrer J K.An Iwatsubo-base solution for labyrinth seal: comparison to experimental results[J].Journal of engineering for gas turbines and power,1986,108(2):325-331.
[5]Yucel U.Calculation of leakage and dynamic coefficients of stepped labyrinth gas seals[J].Applied mathematics and computation.2004,152:521 -533.
[6]Bently D,Muszynska A.Role of circumferential flow in the stability of fluid-handling machine rotors[C].The 5th workshop on rotor dynamic instability problems in high performance turbo machinery,Texas A&M University,1988:1 -5.
[7]陈予恕,丁 千.非线性转子-密封系统的稳定性和Hopf分岔研究[J].振动工程学报,1997,10(3):368 -374.
[8]叶建槐,刘占生.非线性转子-密封系统稳定性与分岔[J].航空动力学报,2007,22(5):779-784.
[9] Li S T,Xu Q Y,Zhang X L.Nonlinear dynamic behaviors of a rotor-labyrinth seal system[J].Nonlinear Dynamics,2007,47:321-329.
[10] Cheng M,Meng G,Jing J P.Numerical study of a rotorbearing-seal system[J].Journal of mechanical engineering science,2007,221(7):779 -788.
[11]李忠刚,孔 达,焦映厚,等.转子-密封系统非线性动力学特性分析[J].振动与冲击,2009,28(6):159-163.
[12] Childs D W.Dynamic analysis of turbulent annular seals based on Hirs lubrication equation[J].Journal of lubrication technology,1983,105(3):429 -436.
Dynamic response and stability of a large scale nonlinear rotor-seal-bearing system
CUI Ying,LIU Zhan-sheng,YE Jian-huai
(School of Energy Science and Engineering,Harbin Institute of Technology,Harbin 150001,China)
Nonlinear dynamic model of a rotor-seal-bearing system with ultra-large-scale dimension for an actual steam turbine was proposed considering the non-linear exciting force of seal,the elastic support force of tilting-pad bearing,the damping force,the imbalance force and the gravity of rotor.The unbalance response of the rotor was numerically calculated with Newmark method.The typical characteristic of self-excited vibration and the threshold speed of instability induced by the seal-force were revealed.The effects of the system parameters on dynamic response and instability were also investigated.The results showed that appropriate increase in rotor damping,seal's radius clearance and axial velocity of seal fluid can improve the stability of the system and raise the threshold speed of instability.The results provided a reference for improving the stability of large steam turbine.
rotor-seal-bearing system;nonlinear;high-dimensional;unbalance response;threshold speed of instability
TH212;TH213.3
A
国家自然科学基金重点项目(10632040)
2009-12-21 修改稿收到日期:2010-03-17
崔 颖 女,博士,讲师,1977年10月生
