论高斯非欧几何学思想的实现途径

陈惠勇

(江西师范大学 数学与信息科学学院，南昌 330022)

0引言

高斯(C.F.Gauss，1777—1855)的非欧几何学思想意在揭示欧氏几何不具有唯一的(物理的)必然性，而其内蕴微分几何学则深刻地揭示了几何空间的非欧本质。高斯的非欧几何研究有两个核心问题［1］:平行线的定义(即第五公设之否定——它与三角形内角之和小于180°的假定等价);绝对长度单位(即高斯所说的常数)。从现代微分几何的观点看，我们知道:第一个问题本质上是角之盈余或亏量的问题(这与高斯-博内定理直接相关)，而绝对长度单位与高斯曲率K密切相关且等于

因此，是否抓住了这两个核心问题就成为我们全面理解高斯的非欧几何学思想与其内蕴微分几何学思想内在本质联系的关键。正如高斯自己于1824年11月8日给陶里努斯(F.A.Taurinus，1794—1874)的信中所写:

三角形的三角之和小于180°，这假定导引到特殊的，与我们的几何完全相异的几何。这几何是完全一贯的，并且我发展它本身，结果完全令人满意。除了某一个常数的值不能先天地予以表示定义以外，在这几何里我能解决任何课题。我们给予这常数值愈大，则愈接近欧几里得几何，而且它的无穷大值会使得双方系统合而为一。

如果宇宙的几何真是非欧的，而且如果这常数的数量级和我们能够得到的对地球或

天体的测量值相差不太远的话，那我们应该可以算出这常数。［2］

高斯的这段话，道出了非欧几何与内蕴微分几何学内在的深刻联系及其本质;同时，也指出了他所说的绝对长度单位(常数)与他的非欧几何学思想的实现途径及其与内蕴微分几何学的内在联系。

本文将高斯的内蕴微分几何学与其非欧几何学研究视为一个完整的、统一的思想体系，这也是作者关于高斯几何学思想的基本认识。因此，我们将高斯的内蕴微分几何学思想置于整个非欧几何学的历史背景中加以比较考察，同时又将高斯早年的非欧几何学研究纳入他所创立的内蕴微分几何学的思想体系之中，从现代微分几何学的视角，通过对原始文献以及相关研究文献的比较分析，探究高斯非欧几何学思想的实现途径。

1 非欧几何学的一个历史疑问

史料表明，高斯于1824年已经得到了欧氏几何与非欧几何之间深刻的内在联系——即“我们给予这常数值愈大，则愈接近欧几里得几何，而且它的无穷大值会使得双方系统合而为一”［2］。高斯在这里所说的“常数值”在欧氏几何与非欧几何之间的内在本质联系上有着重要意义。

那么，关于非欧几何学的一个历史性的疑问就是:为什么高斯不发表自己的研究呢?长期以来，人们一直以高斯在1829年1月27日给贝塞尔(F.W.Bessel，1784—1846)的信札中写到的话作为高斯没有公开发表非欧几何研究的证明:

恐怕我还不能够迅速修改关于这个问题的自己很广泛的研究，使它可以出版，甚至在我的一生里可能不能解决这件事，因为当我发表自己的全部意见时，我害怕会引起波哀提亚人的叫嚣。(［2］，200页)

然而，问题真的是那么简单吗?高斯本人的意图到底是怎样的?我们仔细分析高斯这段话的含义，可以看出:后人更多的是强调后半句的意思，即“当我发表自己的全部意见时，我害怕会引起波哀提亚人的叫嚣”，而简单地认为高斯“这主要是因为他感到自己的发现与当时流行的康德空间哲学相抵触，担心世俗的攻击”(［3］，229页)。M.克莱因(M.Kline，1908—1992)也说道:“高斯也许过分小心，但人们应记得，虽然一些数学家逐渐达到非欧几何研究的顶峰，但大部分知识界还被康德的教条所统治”(［4］，288页)。

但是，1844年11月1日，高斯写信给他的朋友舒马赫(H.C.Schumacher，1780—1850)说:

你在当代哲学家谢林、黑格尔、内斯·冯·埃森贝克和他们的追随者身上看到同样的东西(数学上的无能);他们的理论怎能不使你毛骨悚然?读读古代哲学史，过去的那些伟大人物——柏拉图等等——都提出了一些错误的理论。甚至康德本人也不怎么样。照我看来，他对分析命题与综合命题的区分，也只不过是一些过时的东西罢了(［2］，200 页)。

这表明高斯对于当时流行的康德的哲学观点是持批判态度的，高斯应该是不属于被康德的教条所统治的大部分知识界之范畴的。因而那种所谓的“担心与当时流行的康德空间哲学相抵触”的观点是不成立的。

当我们仔细分析与体会高斯的前半句话的含义:一是“我还不能够迅速修改”，二是“我的一生里可能不能解决”。对比高斯在这一时期创立的内蕴微分几何的基本思想，我们可以看出，其实高斯是另有原因的。这就是说，在高斯看来非欧几何还远远没有达到他所希望的那种成熟到可以发表的程度。高斯一生的工作一再验证了他的座右铭:“少些，但要成熟”(转引自［5］，136页)。

然而，几乎就在同一时期，高斯已经在着手创立他的内蕴微分几何学，并且已经找到了研究“弯曲空间”的一般方法——即从曲面本身的度量出发决定曲面在空间的形状。

因此，笔者认为:关于非欧几何的这一历史疑问，只有在全面比较考察和研究高斯的几何学思想(非欧几何学和内蕴微分几何学)的基础上，才可能有一个比较合理的解释(或历史的重构)。

2 高斯的内蕴微分几何学思想与黎曼《关于几何基础的假设》

黎曼(C.F.Bernhard Riemann，1826—1866)可以说是最先理解非欧几何全部意义的数学家。他创立的黎曼几何学不仅是对已经出现的非欧几何(罗巴切夫斯基几何)的承认，而且显示出了创造其他非欧几何的可能性。黎曼认识到度量是加到流形上去的一种结构，因此，同一个流形可以有众多的黎曼度量。黎曼以前的几何学家只知道曲面的外围空间的度量赋予曲面的诱导度量:dr2=ds2=Edu2+2Fdudv+Gdv2(即第一基本形式)，并未认识到曲面还可以独立于外围空间而定义，可以独立地赋予度量结构，黎曼认识到这件事有着非常重要的意义。他把诱导度量与独立的黎曼度量两者区分开来，从而创造了以二次微分形式(即黎曼度量):

为出发点的黎曼几何，这种几何以各种非欧几何作为其特例。

黎曼的上述构想必定是与高斯的深刻影响分不开的①黎曼几何的产生则是受到了多方面的影响，其几何学思想的三个主要来源是:数学、物理和哲学思想的影响。见［6］．［6］。首先，高斯是黎曼的老师，师生之间的深刻影响是必然的。在高斯的指导下，黎曼于1851年完成他的博士论文《单复变函数一般理论基础》，其中给出了单值解析函数的严格定义，同时引进了一个非常重要的概念——“黎曼曲面”。黎曼曲面本身就是一个流形，对于黎曼曲面的研究已经构成现代数学的一个重要分支，它涉及分析、几何和拓扑等现代数学的广大领域。

其次，当我们深入地分析黎曼《关于几何基础的假设》的内容及其蕴含的深刻思想，就可以发现高斯的思想对黎曼的影响是非同一般的。黎曼在这篇著名的演说中所要解决的两个核心问题是:一是建立n度广义流形的概念，另一个问题就是建立n维流形上可容许的度量关系。黎曼在他的演讲中三次提到高斯的工作。

第一次是在演讲的第一部分:“n度广义流形的概念”，黎曼说道:

因为解决这个问题的困难主要是概念上而非构造上的，而我对这个困难的哲学方面思考得很少;况且除了枢密顾问高斯发表在他的关于二次剩余的第二篇论文及在他写的纪念小册子之中的非常简短的提示和Herbart的一些哲学研究外，我不能利用任何以前的研究。(［7］，602页)

从这里我们可以看出，黎曼提到高斯“非常简短的提示”，说明高斯已经有了至少是模糊的或初步的流形的观念，并且这种观念对黎曼是有所启发的。

第二次是在演讲的第二部分:“n维流形上可容许的度量关系”，黎曼说道:

关于这个问题的两个方面(指一个流形能容许的度量关系和确定度量关系的充分条件)的基础包含在枢密顾问高斯关于曲面的著名论文中。(［7］，605页)这里所说的著名论文就是指高斯的《关于曲面的一般研究》。

第三次是在演讲的第二部分的第2小节中，黎曼说到在一般流形上用作衡量曲面片在一点偏离平坦的程度的数值时，再一次提到高斯的工作“当这个数值乘以时得到的值就是枢密顾问高斯所谓的曲面的曲率”(［7］，607页)，这里的数值就是现在所称的“高斯曲率”。以上分析足以证明高斯的思想对黎曼的深刻影响。

从黎曼的几何学构想上看更能看出黎曼几何思想与高斯内蕴几何学思想的一脉相承。首先，黎曼几何学的出发点是所谓的黎曼度量它与高斯的出发点第一基本形式dr2=ds2=Edu2+2Fdudv+Gdv2相比较，我们明显地看出黎曼度量是高斯的第一基本形式(相当于n=2的情形)的高维推广，当然黎曼用的是张量的记号。

事实上，用现代微分几何学的观点来看我们知道，二维情形的黎曼几何学就是高斯的内蕴微分几何学。因此，黎曼的几何学思想不仅对高斯内蕴几何学思想有继承更有发展，而这种思想的一脉相承的更为本质的体现，则是黎曼对于n维流形在一点的一个曲面方向的曲率的形象解释，他完全遵循着高斯的思路，黎曼指出:

……前一种解释蕴含着曲面的两个主曲率半径的乘积在曲面不伸缩的形变时是不改变的这个定理，后一种解释蕴含着在每一点的无穷小三角形的内角和超过两个直角的部分和它的面积成比例。为了给出n维流形在一点的一个曲面方向曲率的形象解释，我们必须由这样一个原则出发，即从一点发出的最短线被初始方向完全确定。(［7］，609 页)

这正是高斯曲面论的两个核心定理，即高斯的绝妙定理和高斯-博内定理，而且黎曼所遵循的原则也正是高斯研究的出发点。可见，黎曼的几何学构想与高斯的内蕴微分几何学思想在本质上是一致的。

3 常数(绝对长度单位)高斯曲率曲面与非欧几何的实现

黎曼几何学思想不仅是对高斯内蕴几何学思想的继承，更重要的是对高斯内蕴几何学思想的发展。由于黎曼认识到度量是加到流形上去的一种结构，因此，同一个流形可以有众多的黎曼度量。黎曼在他的就职演说《关于几何基础的假设》中，特别地考虑了所谓的常曲率流形，这种流形的度量关系仅与曲率的值有关，如果设曲率为α，那么度量ds可取下面的形式(［7］，609页):

这是黎曼的演讲中出现的唯一的一个数学公式。这里的常数α就是高斯曲率在高维情形的推广——称为黎曼曲率张量。因而，具有上述度量的流形就是所谓的常曲率流形(在n=2的情形，就是所谓的常数高斯曲率曲面)。我们可以证明:当黎曼曲率张量α＞0时，就是球面几何(又称为正常曲率空间的几何);当黎曼曲率张量α=0时，就是欧氏几何;而当黎曼曲率张量α＜0时，就是罗巴切夫斯基几何(称为负常曲率空间的几何或双曲几何)。

为了更好地理解黎曼的上述思想，我们在二维流形上来说明常曲率“空间”中的测地线的性状以及非欧几何的实现途径［8］。

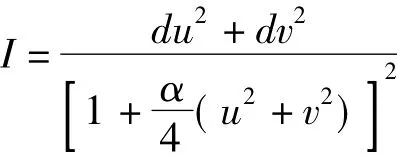
考虑第一基本形式为:的常数高斯曲率曲面(这就是黎曼考虑的常曲率流形)。通过计算可以知道，该曲面的高斯曲率K为常数α。当α≥0时，该抽象曲面可以定义在整个(u，v)平面上;当α＜0时，该抽象曲面的定义域是:

当α=0时，则I=du2+dv2，此时的度量就是欧氏平面上的普通度量(就是由勾股定理所给出的度量)，它上面的测地线就是普通的直线，而这个抽象曲面的几何就是普通的欧氏几何。由于高斯曲率α=0，由高斯-博内定理可知，在这个抽象曲面上其三角形的内角和等于180°。

当α＞0时，则这个抽象曲面可以看作E3中半径为的球面通过从南极向球面在北极的切平面作球极投影所得到的像，如图1所示。

图1 球极投影

具体地说，这个投影的表达式是

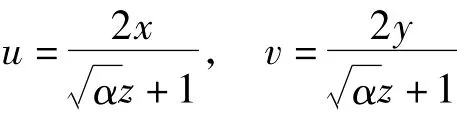
或者

在球面上，测地线就是大圆。很明显，这些大圆周在球极投影下的像是(u，v)-平面上以原点为中心、以为半径的圆周C，以及所有的经过圆周C的一对对径点的直线和圆周，如图2所示。

很明显，在这样的抽象曲面上，任意两条测地线都是彼此相交的。因而，这个抽象曲面上的几何就是球面几何(非欧氏几何)。由于高斯曲率α＞0，由高斯-博内定理可知，在这个抽象曲面上由测地线构成的三角形的内角和大于180°。球面(高斯曲率等于1)上的测地三角形，如图3所示。

的抽象曲面称为Klein圆。可以证明:在Klein圆内的测地线是圆内与圆周正交的圆弧或直径，如图4。

很明显，在这样的抽象曲面上，过“直线”外一点可以作无数条“直线”与已知“直线”不相交。因此，在Klein圆内，欧氏几何的“平行公设”——过直线外一点所引的与该直线平行的直线有且只有一条——不再成立。这个抽象曲面就是非欧几何的Klein模型，它比非欧几何的Beltrami模型(相当于高斯曲率α=－1的情形，对应的抽象曲面叫伪球面)更加简单明了地指出了，在这样的抽象曲面上，普通的欧氏几何的事实就成了罗巴切夫斯基几何的定理。这个抽象曲面上的几何就是双曲几何。由于高斯曲率α＜0，由高斯-博内定理可知，在这个抽象曲面上由测地线构成的三角形的内角和小于180°。伪球面(高斯曲率α=－1)上的测地三角形，如图5所示:

以上，我们从现代微分几何的观点，考察了高斯非欧几何研究的实现途径与内蕴微分几何的内在联系。从中我们可以清楚地看到:高斯-博内定理在联系其非欧几何研究的两个核心问题之间的桥梁作用和特殊意义。高斯-博内定理从本质上揭示了从欧氏几何学到非欧几何学的发展历史，这一历史的发展过程，实际上就是从平面几何到常数高斯曲率曲面上的几何学的发展过程，更一般地，到抽象曲面上的几何学的发展过程。在这一推广过程中，直线换成了测地线(最短线)，相对曲率换成了测地曲率，其根本的不同之处在于所论的“空间”的高斯曲率的不同，也就是“空间”的度量结构不同。欧氏“空间”的高斯曲率为零，由高斯-博内定理有A+B+C=π，这就是“三角形的三内角之和等于180度”的定理;非欧几何的“空间”的高斯曲率不为零，由高斯-博内定理有“三角形的三内角之和不等于180度”，因此该“空间”是弯曲的!由于高斯曲率的符号的不同，影响了“空间”中的测地线的性状不同，从而也决定了测地三角形的内角和的不同。

因此，高斯-博内定理对于人类关于空间性质的认知特别是对于空间的非欧本质的认识就有着重要的意义。

一般地，对于三维常数高斯曲率空间，我们有以下三种情形:曲率为正常数——黎曼非欧几何(球面几何);曲率为负常数——罗巴切夫斯基非欧几何(双曲几何);曲率恒等于零——欧几里得几何。

4 量地与测天——高斯非欧几何的验证

从上面的分析和比较，我们可以看到高斯非欧几何研究的实现途径与他的内蕴微分几何思想的内在联系。当然，高斯本人并未完全地实现这一过程。但是，高斯却奠定了通向这一过程的理论与实践两方面的基础。

在理论上，高斯已经有了实现其非欧几何研究的内蕴微分几何学途径的思想，高斯在其一般研究［9］的第20节中得到了著名的高斯-博内定理之后，在接下来的第21节直到第29节全部用于比较定理的证明。在这些比较定理中，一方面，高斯把单个的角(不仅仅是角度之和)与欧几里得平面上具有同样长度的直边形三角形的角进行比较;另一方面，高斯还把曲面上测地三角形的面积与欧几里得平面上具有同样长度的直边形三角形的面积进行比较。从这我们不难看出高斯的真正用意。

在实践上，高斯利用他的实际大地测量工作——量地与测天——亲自验证他发现的非欧几何。高斯为了说明他的角度比较定理和面积比较定理，进行了实地的大测地三角形的测量。高斯在《关于曲面的一般研究》的第28节，附了一个当时他所做的三角测量结果的记录，其中三个顶点分别为Hohenhagen(H)，Brocken(B)及lnselsberg(I)的山顶;H，B，I两两的距离分别为69，85及107公里，几近直角三角形。高斯利用他自己发明的日光发射信号器(heliotrope)得到山顶之间的由光线构成三角形HBI，决定H，B，I的角度，测得三角和H+B+I为180°，因而与欧氏几何符合;然后，再测量由测地线得到的地球表面上对应的测地线三角形，并算出其角度H1，B1及I1，此三角和超过180°约14.85348″。虽说微不足道但确实超过180°，在三个顶点盈余的量分别是:

这三数与其平均值间的差异，与地球近北极时较平有关。差异显然小于0.0002″，故高斯结论说:“即使是在地球表面上，这些角度可以测量到的巨大三角形上，这种差别通常是太小而难以觉察的”。［9］

后来的数学家揣测，这些测量还有额外的目的，就是检查由光线造成的三角形HBI的内角和与欧几里得的值180°是否有偏差。

F.克莱因(Felix.Klein，1849—1925)指出:

在高斯的这些工作(非欧几何学)里，完全看不到高斯在他的无畏的思想面前退缩。从他与Olbers，Schumacher，Bessel以及其他人的通信，连同他的一些未公开发表的论文，毫无疑问地表明高斯已经掌握了非欧几何学的思想。虽然关于这个成就高斯一个字也没有发表过，但是非欧几何学思想，在他的任何工作中都没有离开过，这一点从他的信件中清楚地流露出来。就此而言，上面说过的他测量光线所成的三角形，又有了新的意义。(［10］，14页)

我们认为，联系前面所引的1824年11月8日高斯给Taurinus的信所表达的深刻含义，以及1827年3月1日高斯给他的朋友奥伯斯(Heinrich W.M.Olbers，1758—1840)的一封信中所说的:

在实际当中，这(指地球表面测地三角形的不同角的修正值的差异)当然一点也不重要，因为它对于地球上可以测量到的最大的三角形来说是微不足道的;然而，科学的尊严要求我们要清楚地理解这个不等量的本质。(［2］，188页)

特别是，结合 19世纪后期贝尔特拉米(E.Beltrami，1835—1900)，F.克莱因(F.Klein，1849—1925)，庞加莱(H.Poincare，1854—1912)等关于非欧几何的发展与确认的实现途径来看，我们认为这种揣测是可以成立的。

如果上述认识能够成立的话，那么我们是否可以认为:不管是量地或测天，高斯的真正用意是验证他的非欧几何。因为高斯是把几何看成和力学一样的实证科学，到底哪一种几何为“真”，在“现实”中存在，他觉得只有实验能够解答。因而，高斯企图用他那个大测地三角形为实证，来发现宇宙空间与欧氏几何的偏差。高斯的一生工作计划严谨周密，特别是在他的大地测量工作中更表现出非凡的组织才能。因此，我们认为，在当时来讲只有他自己心里有数，但历史地看，那么结论是毫无疑问的［11］。

值得注意的是，莫里斯·克莱因(Morris Kline，1908—1992)在关于高斯的内蕴微分几何学与非欧几何学思想的内在联系上，其观点是自相矛盾的，关于高斯的内蕴微分几何学，他指出:

高斯的工作意味着，至少在曲面上有非欧几何，如果把曲面本身看成是一个空间的话，高斯是否看到他的曲面几何学的这种非欧几何学的解释，那就不清楚了。(［4］，308页)

而在同一专著中，关于高斯的非欧几何学思想，他又指出:

为了检验欧几里得几何学和他的非欧几何的应用可能性，高斯实际测量了由Hoherhagen、Brocken和Inselberg三座山峰构成的三角形的内角之和，三角形三边为69，85与197公里。他发现内角和比180°超出14″85。……如高斯所认识到的，这个三角形还小，又因在非欧几何中，亏值与面积成正比，只有在大的三角形中才有可能显示出180°与三角和有任何差距。(［4］，289页)

然而，我们知道，高斯在他的《关于曲面的一般研究》的第21—29节，正是着力阐述直线型三角形(欧氏几何学的)和测地三角形(非欧几何学的)之间的角度比较定理和面积比较定理，高斯将其“检验欧几里得几何学和他的非欧几何学的应用的可能性”的实际地理测量的结果记录于他的一般研究之中，并构成其中的第28节的内容［9］。

今天，有很多经验与事实(如爱因斯坦的广义相对论)，能够证明现实世界的几何是非欧的;但是由于差异很小，以至于在实际生活中，例如说筑路、造桥、开隧洞时，可以不去理它。正如高斯所说:

一般地说，在地球表面上所有可以测量到的三角形内，这种误差太小而难以察觉(error generaliter loquendo erit quinti ordinis，sed insensibilis in omnibus triangulis，qualia in superficie telluris dimetiri licet.)。［12］

这是高斯《关于曲面的一般研究》一文的最后一句话。同时，高斯在他的论文摘要中指出:

……但是哪怕曲面与球面仅是略有差别，这种修正也不应忽略。因此，具体算出修正值并由此说明在地球表面测地三角形的情形下这些微不足道的偏差，是十分重要的。(［13］，569页)

这句话与我们前面所引的高斯于1824年11月8日给陶里努斯的信中的话——“我们给予这常数值愈大，则愈接近欧几里得几何，而且它的无穷大值会使得双方系统合而为一”——可以说是遥相呼应。

肯定的观察与实验来自原子物理与天文学。宇宙几何的绝对单位长度也许可以得自于星际距离及星际质量的测量。我们不知道我们所看到的宇宙，其非欧几何的高斯曲率是多少;我们甚至也不知道它是正是负，到处存在于这个银河世界中的宇宙曲率的计算，依然是今天的科学家们最重要的工作。

根据爱因斯坦的广义相对论，宇宙的真实几何与欧氏几何间的相差程度可以据之表示出来。我们可以从实验中计算出三条在重力场影响下的光线所构成的三角形的内角和。高斯所测量的三角形HBI的角之差实在太微小了，以至于高斯那时候和我们现有的光学仪器都无法测出，差异的数量级为10－17秒角，即小数点后有十六个零。但是，高斯却认识到:

如果宇宙的几何真是非欧的，而且如果这常数的数量级和我们能够得到的对地球或天体的测量值相差不太远的话，那我们应该可以算出这常数。［2］

5结语

通过上述比较研究，我们认为:高斯完全看到了这两种几何的内在联系，并且完全看到了曲面本身(即把曲面本身作为一个空间)的这种非欧本质。高斯于1827年发表的《关于曲面的一般研究》不仅奠定了内蕴微分几何学的基础，标志着内蕴微分几何学的诞生，而且提出了几何学历史上的一个具有革命性意义的概念——即一个曲面本身就是一个空间，寻求到了解决“从曲面本身的度量出发决定曲面在空间的形状”这一重大理论问题的一系列重要方法，提出了高斯映射、高斯曲率、总曲率等重要概念，证明了高斯曲率在等距变换下的不变性(绝妙定理)以及由高斯曲率的符号进一步将空间的曲面进行分类，而高斯-博内定理又进一步揭示出空间的非欧本质。

因此，高斯的内蕴微分几何学本质上已经蕴含了他的非欧几何学研究的基本思想，实现了他的非欧几何研究中的两个核心的问题，阐述了两者的深刻的内在联系(高斯-博内定理)。更重要的是，高斯的内蕴微分几何学思想为非欧几何学的发展与最终的确认指明了一条微分几何的途径，而这条道路最终引导着黎曼、贝尔特拉米、F.克莱因、庞加莱等伟大的数学家走向并最终实现了非欧几何学的发展与确认的艰难历程。

致 谢本文得到我的导师李文林先生的悉心指导，并得到先生主持的基金项目支持，在此表示衷心的感谢!

1 陈惠勇．高斯的内蕴微分几何与非欧几何［J］．西北大学学报(自然科学版)，36(6):1028—1032．

2 Gauss C F．Werke［M］Ⅷ．London:Herausgegeben von der K;Gottingen:Gesellschaft der Wissenschaften zu Gottingen，1900．

3 李文林．数学史概论［M］．第二版．北京:高等教育出版社，2002．229．

4 (美)莫里斯·克莱因．古今数学思想(第三册)［M］．上海:上海科学技术出版社，2002．

5 Dombrowski P．Differential Geometry—150 Years After CARL FRIEDRICH GAUSS'Disquisitiones Generales Circa Superficies Curves［J］．Astérisque，1979，62:97—153．

6 邓明立，阎晨光．黎曼的几何思想萌芽［J］．自然科学史研究，2006，25(1):66—75．

7 黎曼．关于几何基础的假设［A］．李文林数学珍宝——历史文献精选［C］．北京:科学出版社，1998．601—613．

8 陈维桓．微分几何初步［M］．北京:北京大学出版社，2003．185—187．

9 高斯．关于曲面的一般研究［J］．陈惠勇译，苏阳校．数学译林，2008，27．

10 F．克莱因．数学在19世纪的发展［M］．第一卷．齐民友译．北京:高等教育出版社，2010．

11 Hall T．高斯——伟大数学家的一生［M］．第三版．田光复等译．新竹:凡异出版社，1986．

12 Gauss C F．Werke［M］Ⅳ．London:Herausgegeben von der K;Gottingen:Gesellschaft der Wissenschaften zu Gottingen，1880．

13 高斯．《关于曲面的一般研究》摘要［A］．李文林．数学珍宝——历史文献精选［C］．北京:科学出版社，1998．565—570．