工程结构随机地震响应分析的大质量扩阶解法

曹春青

工程结构随机地震响应分析的大质量扩阶解法

曹春青

为简化求解平稳过滤白噪声地震动激励下工程结构动力响应的求解公式，提出一种大质量扩阶解法，将输入简化为白噪声模型。结合复振型分解理论，即可基于白噪声过程激励下单自由度结构动力响应的求解公式获得结构在复杂地震动作用下的随机动力响应，并指出该方法可避免繁琐的积分运算，求解速度快，值得推广应用。

结构工程，扩阶，大质量，地震响应，随机分析

0 引言

在平稳白噪声过程激励下，工程结构的线性动力响应的功率谱和方差通常都能求得解析解。不过，对于一些其他常用的复杂平稳随机过程，求解过程将非常复杂，大多数情况下甚至很难得到解析解。不过，当随机过程的功率谱可以由白噪声过程过滤得到时，则有可能通过扩展结构系统自由度阶数而降低求解积分运算的难度。方同曾提出一种扩阶解法求解平稳过滤白噪声过程激励下结构的随机响应［1，2］，该方法将过滤层在白噪声激励下的动力平衡方程与上部结构在过滤层相应的输出结果激励下的方程联立起来，组成一个在白噪声过程激励下的扩阶系统。由于此扩阶系统中上部结构受到过滤层的作用，但过滤层不接受上部的反馈作用，所以扩阶系统的参数矩阵是非对称的，扩阶系统也仅仅是形式上的联立，并不对应任何实际的物理模型，本文称之为“数学扩阶解法”。一些学者在随机振动问题的研究中采用了类似的方法：姚昌仁等人采用扩阶解法研究有色噪声激励下结构随机响应的灵敏度问题［3］、侯志强等人采用此法计算有色噪声激励下的迟滞系统的随机响应［4］、李创第和李暾等人采用此法研究建筑结构调频减振［5，6］和隔震问题［7］、吴存利、冷小磊和方同采用此法研究TMD减震问题［8］。

由于数学扩阶解法形成的扩阶矩阵是非对称的，因而需要求解左、右特征向量，本文提出一种大质量扩阶解法，可以避免该问题。本文先介绍数学扩阶解法的步骤，给出地震工程中常见平稳震动模型的扩阶解法和数值算例的验证，并对相关问题进行了讨论。

1 结构平稳响应的大质量扩阶解法

设某加速度过程g(t)可以由平稳白噪声加速度过程激励下的二阶系统的动力响应给出，称此二阶系统为过滤层，设过滤层自由度为l，则其动力平衡方程为：

其中，Mn×n，Cn×n，Kn×n，{x}n分别为上部结构的质量、阻尼和刚度矩阵及节点位移向量，Mn×n为对角矩阵;In为单位列向量。下面分别给出当上部结构的输入为过滤层绝对加速度响应时的大质量扩阶解法。

如果g(t)是式(1)中过滤层第i个节点的绝对加速度(金井谱属此类情况［9，10］)，联立式(1)，式(2)可得：

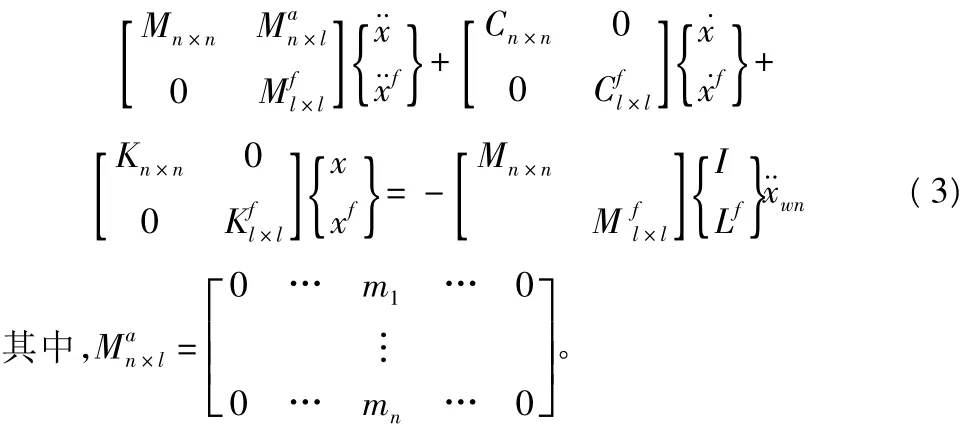
上式等号左侧的上标“a”为该矩阵是添加到原质量矩阵中去的，等式右端的m1，mn为Mn×n中的对角元素。式(3)与式(1)，式(2)是完全等价的，但是式(3)所示的扩阶系统的输入为白噪声过程，采用振型分解解耦后，其求解公式将比直接求解式(2)简单的多。这实际上就是文献［2］介绍的数学扩阶方法，只不过文献［2］中是先采用复模态分析理论将式(1)，式(2)转换为一阶微分系统后再联立的，本文是直接联立的二阶微分系统。显然式(3)中的扩阶质量矩阵是非对称的，本文对式(3)试做如下变化强迫使其对称：

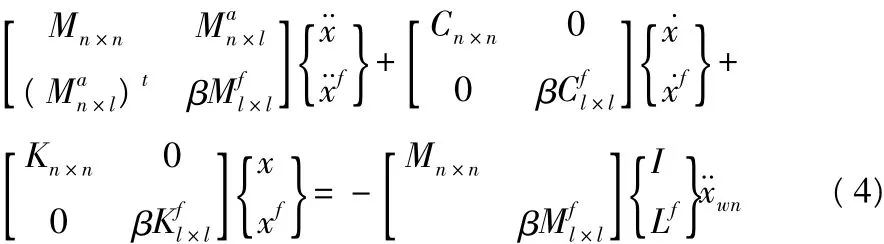
其中，β为质量放大倍数。上述变换相当于保持式(2)不变，而式(1)变为：

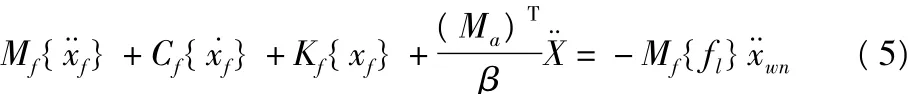
式(5)是白噪声作用下二阶系统，由于扩阶阻尼矩阵通常不再满足比例假定，所以需要采用复模态振型分解方法进行降阶［11］。这就是本文提出的大质量扩阶解法。

2 平稳随机响应的算例

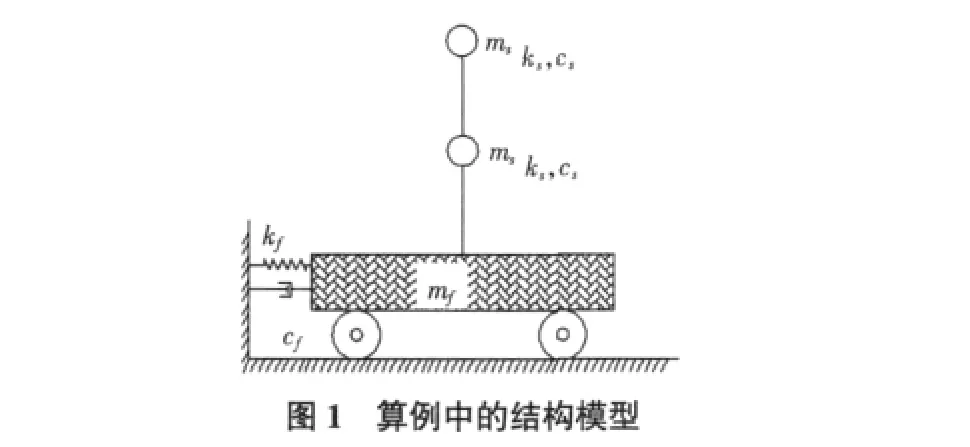
下面考察采用上述大质量扩阶解法计算一个二自由度结构在功率谱为金井清模型的平稳过滤白噪声过程激励下的随机响应的精度。结构简图如图1所示，其中，ms=3 kg，ks=200 kN/m，cs=3.963 4 kN·s/m。

金井清模型是单自由度振子在白噪声作用下的绝对加速度响应，为行文简洁，本文称功率谱为金井清模型的平稳随机过程为金井清过程，当随机过程的功率谱为其他功率谱模型时依此类推。当输入加速度过程为金井清过程时，应采用式(4)所示公式求解，此算例的具体公式为：

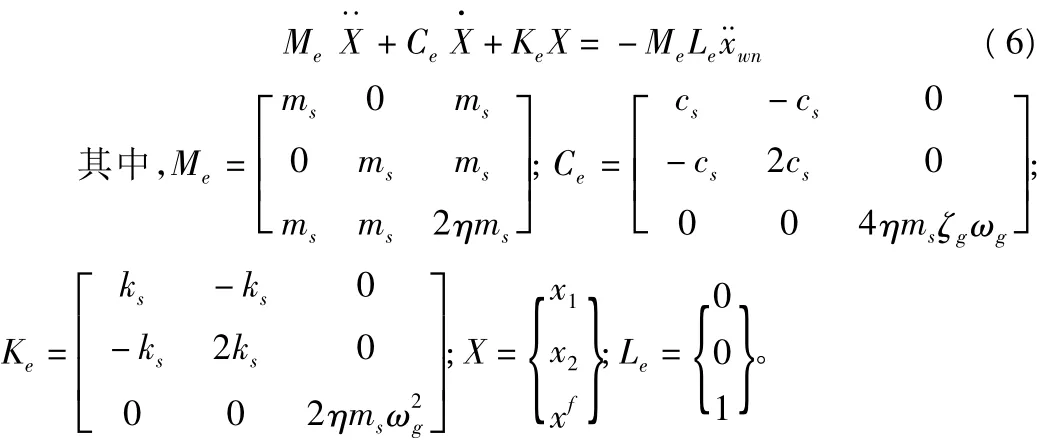
值得指出的是：式(6)右端的荷载位置向量为［0，0，1］t，而不是单位列向量。先将式(6)转换为如下一阶形式：

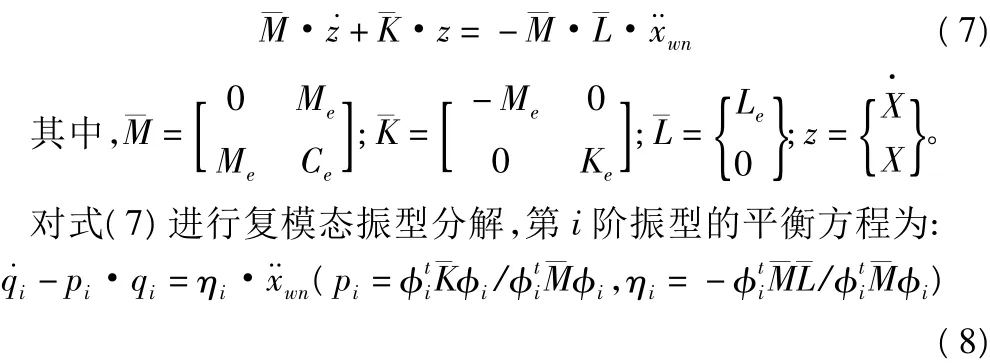
其中，pi为i阶复特征值，与之相应的特征向量记为φi;ηi为振型参与系数;qi为复振型位移且有：

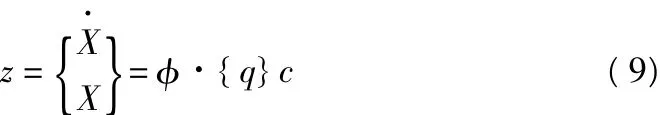
由式(8)可知第i阶振型的频响函数为Hi(ω)=1/(－pi+ iω)，则结构位移和速度响应功率谱矩阵可写为：

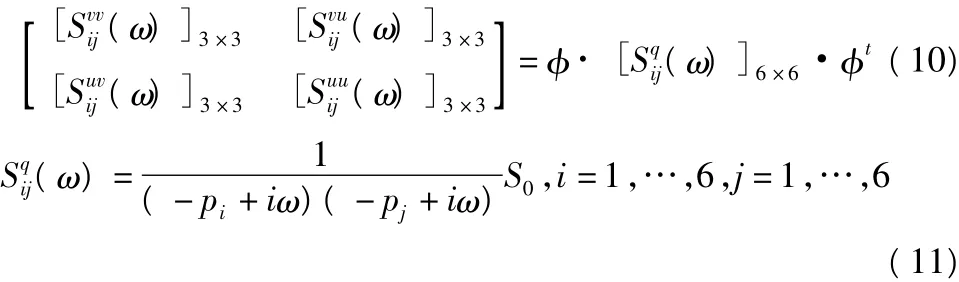
式(10)给出了计算扩阶系统位移和速度响应功率谱的公式，下面讨论加速度的计算方法。由式(8)可知，φ·η=－¯L，所以下式成立：

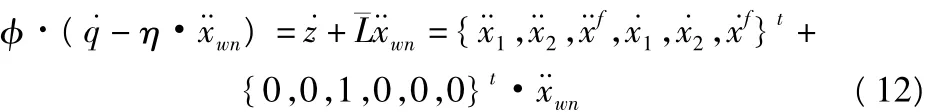
上式右端给出了上部结构的速度、相对加速度反应和过滤层的绝对加速度、速度反应。而上式左端显然等于φ·(pi·qi)，那么过滤层的绝对加速度功率谱可由下式给出：

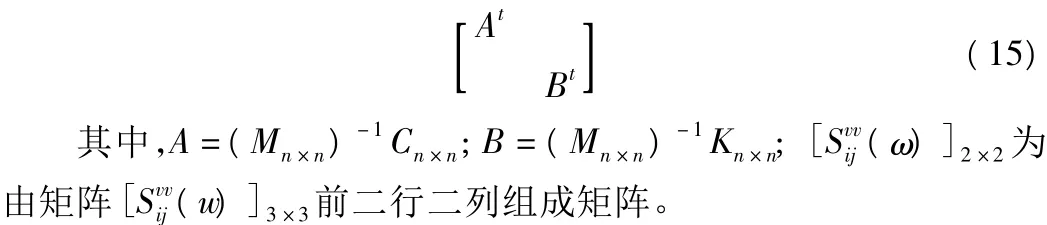
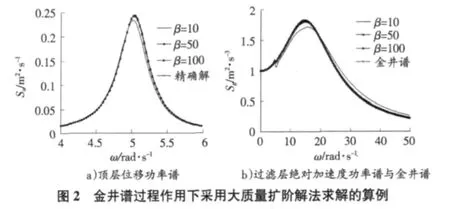
图2显示的是顶层位移和过滤层绝对加速度功率谱。算例中ωg=18 rad/s，ζg=0.6，β为过滤层质量与上部结构质量之比。图2中理论精确解采用直接频响函数法求解。从图2中可以看出，当β=100时，大质量扩阶解法给出的结果与理论精确解十分接近。

3 结语

本文介绍一种求解平稳过滤白噪声激励下工程结构动力响应的大质量扩阶解法，采用该解法得到的扩阶系统的参数矩阵是对称阵，与不考虑土结相互作用的理论解相比，该算法的计算结果理论上是近似的，但是具有非常高的精度，完全能够满足工程要求;考虑地震地运动的实际情况后，该算法实际上是更为合理的。

［1］ Fang.T，Wang.Z N.Stationary Response Due to Arbitrarily Filtered White Noise Excitation［J］.Journal of Northwestern University.English Extra Issue，1987，3(1)：41-48.

［2］方 同.工程随机振动［M］.北京：国防工业出版社，1995.

［3］ 姚昌仁，麻永平.结构随机激励的响应灵敏度分析［J］.力学学报，1990，22(4)：438-445.

［4］ 侯志强，李 跃.迟滞系统受随机激励的响应计算［J］.应用力学学报，2003，20(4)：101-104.

［5］李创第，李 暾，黄天立，等.高层建筑TMD风振控制分析的复模态法［J］.振动与冲击，2003，22(2)：1-4.

［6］ 李 暾，李创第，章本照.带TLD结构随机风振响应的解析解［J］.哈尔滨工业大学学报，2003，35(4)：437-440.

［7］ 李创第，丁晓华，陈俊忠，等.基础隔震结构基于Clough-Penzien谱随机地震响应分析的复模态法［J］.振动与冲击，2006，25(5)：39-43.

［8］吴存利，冷小磊，方 同.随机结构地震响应的TMD控制［J］.西北工业大学学报，2007，25(2)：305-311.

［9］ Kanai.K.Semi-empirical Formula for the Seismic Characteristics of the ground Motion［R］.Japan：Earthquake Research Institute University of Tokyo，1957：309-325.

［10］ Tajimi.H A.Statistical Method of Determining the Maximum Response of Building Structure During an earthquake［J］.2end Word Conference on Earthquake Engineering，1960 (35)：781-798.

［11］ Zhou X Y，Yu R F，Dong D.Complexmode superposition algorithm for seismic responses of non-classically damped linear MDOF system［J］.Journal of Earthquake Engineering，2004，8 (4)：597-641.

On largemass expanding rank method of random earthquake response analysis in project structure

CAO Chun-qing

In order to simplify the solving formula for the engineering dynamic response under the stationary filtered white noise seismicmotions，the paper points out the largemass expanding rank method to simplify the input to be the white noisemodel，combines the complexmode decomposition theory，indicates the random dynamic response of the structure can be obtained in the complicated seismic effect for the solving formula of the single degree of freedom structure under the white-noise process，and points out themethod can avoid the complicated integral operation and have speedy solution speed，so it can be further applied.

structural project，expanding rank，largemass，earthquake response，random analysis

TU311.3

A

1009-6825(2011)17-0051-03

2011-02-24

曹春青(1978-)，女，工程师，中铁电气化局集团北京建筑工程有限公司，北京 100000