李超三系的实现

张永平， 鲁亚男

(沈阳化工大学数理系，辽宁沈阳110142)

李超三系作为一种代数体系，最初源于解物理上的Yang-Baxter方程.Susumu Okubo在研究Yang-Baxter方程的过程中发现了这个体系，并将其命名为李超三系.李超三系与其他诸多代数体系相联系，尤其与李超代数关系极为密切.由文献［1］可知，李超代数可生成李超三系.目前对quasi-classical李超三系已有文章对其进行研究.但对李超三系的结构、导子、表示论等一系列问题的研究还不够完善.本文对李超三系的结构做了一些研究.

1 李超代数及三系的定义

定义1［2］如果超代数L=L0－⊕L1－有一个括积运算［，］满足如下条件:

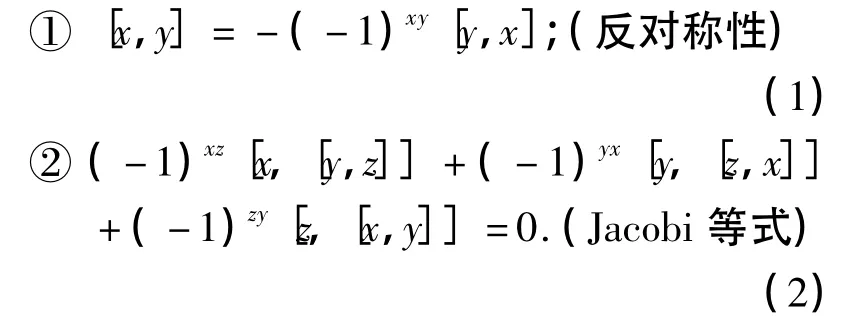
则被称为一个李超代数.

定义2［3］一个Z2-阶化向量空间V被称为一个李超三系，如果它有一个三角积［4］:V⊕V⊕V→V满足如下条件:

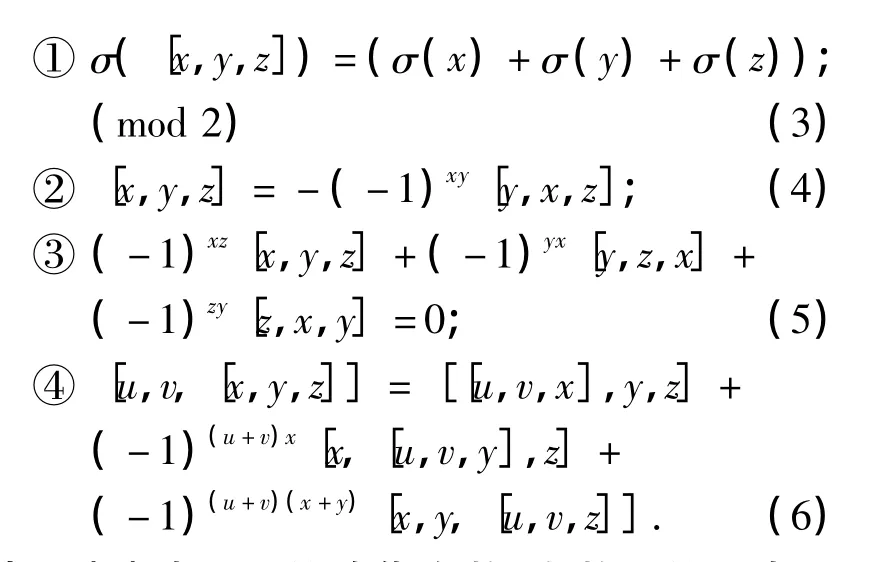
其中，σ(x)表示x的阶化次数，指数上的x表示x的阶化次数.

2 相关的等式

通过应用(4)式对(6)式做适当的变形，可得如下几个等式:

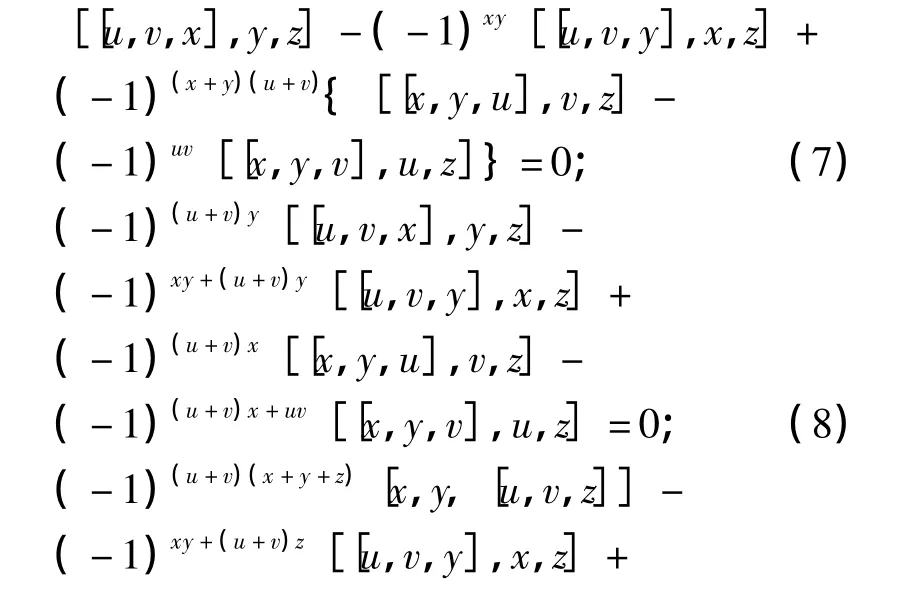
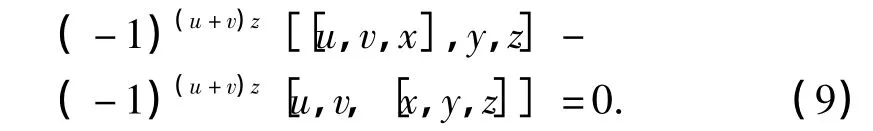
再应用(5)、(7)、(8)、(9)式，有

其中，Q、R是(10)式中前4项通过(u，v)，(x，y)，(z，k)的循环得到.

3 李超三系的实现

由文献［1］可知，在李超代数L上令［x，y，z］=［［x，y］，z］，则L在此定义下是一个李超三系.下面将说明任意一个李超三系均可由这种方法得到.

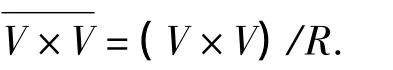
需要说明向量空间L=V⊕V×V可以构成一个李超代数.

3.1 定义的合理性

在L中，如果∀a，b∈V，定义

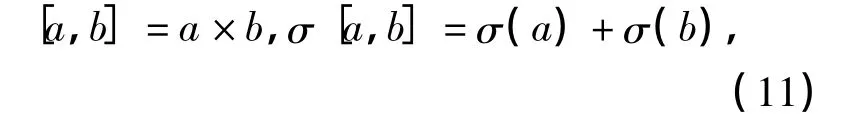
如果∀a，b，c，d∈V，定义

如此定义的［，］是双线性的.

在(12)式中，左边若每一个因子是零，那么右边也是零.因为设∑［a，b］=0，根据商空间定义∑a×b∈R，由R的定义得∑［a，b，c］=0.因此，(12)式的定义是合理的，即单值的.

类似可证，(13)、(14)式的定义也是合理的.

定义L中的一般乘法运算［u，v］，a，b，c，d，e，f∈V，

令u=a+∑［b，c］，v=d+∑［e，f］，定义

由(12)～(14)式可知此定义是合理的.

3.2 验证L是一个李超代数

首先，说明3.1中的定义［，］是反对称的，即需验证∀a，b，c，d∈V时下面等式成立.

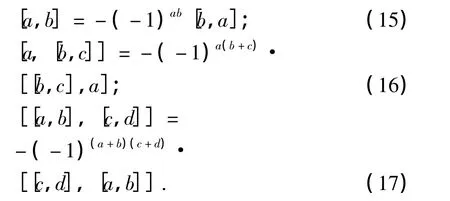
在李超三系中有

［a，b，x］=－(－1)ab［b，a，x］，即

［a，b，x］=－(－1)ab［b，a，x］=0，

则有

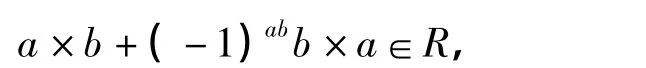
所以(15)式成立.

由(12)和(13)式可知(16)式成立.

将(17)式变形，得到

由(7)式可知(17)式成立.

其次，说明Jacobi等式成立.需要考虑4种情形:

1)所有的元素均在V中;

2)两个元素在V中，一个元素是［a，b］的形式;

3)一个元素在V中，两个元素是［a，b］的形式;

4)所有元素均是［a，b］的形式.

第1种情形:∀a，b，c∈V，由(12)式，有［［a，b］，c］=［a，b，c］，再由(5)式直接可得到

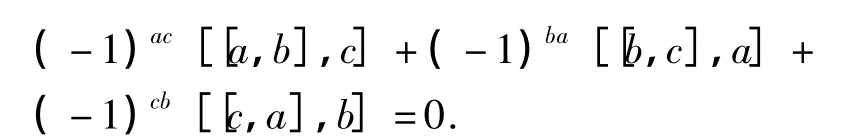
第2种情形:∀a，b，c，d∈V，需要证明

将其变形得

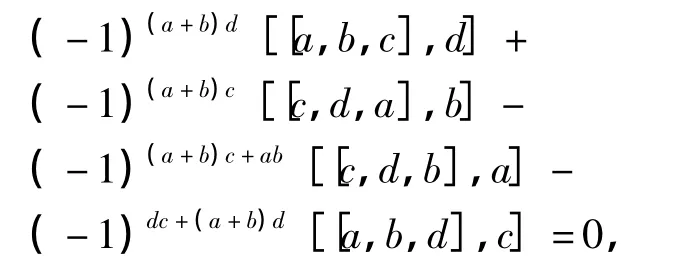
由(8)式可知上式成立.

第3种情形:u=［a，b］，v=［c，d］，w=e，∀a，b，c，d，e∈V，需要证明

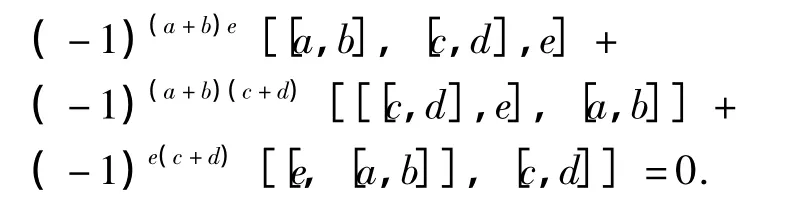
将其变形得

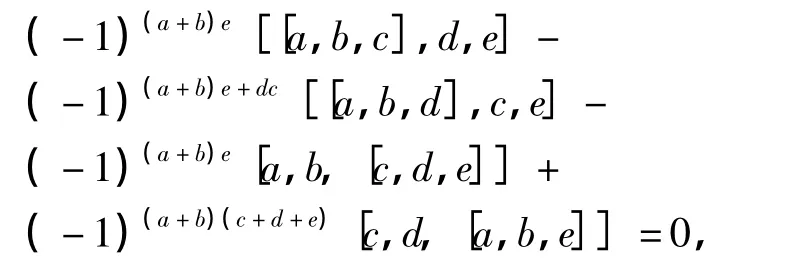
由(9)式可知上式成立.

第4种情况:u=［a，b］，v=［c，d］，w=［e，f］，∀a，b，c，d，e∈V，需要证明

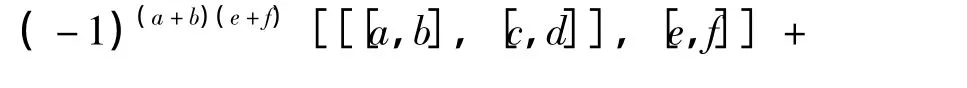
将其变形得

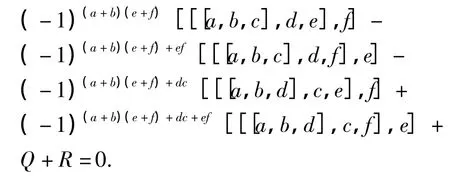
其中，Q、R是上式中前4项通过(a，b)，(c，d) (e，f)的循环得到.

由(10)式可知上式成立.

综上所述及文献［1］，得到下面定理:

定理 李超代数与李超三系是一一对应的.

［1］ Okubo S.Parastatistics as Lie-supertriple Systems［J］.J.Math.Phys，1994，35(6):2785－2803.

［2］ Kac V G.Lie Superalgebras［J］.Advances in Mathematics，1977，26:8－96.

［3］ Okubo S，Kamiya N.Quasi-Classical Lie Superalgebras and Lie Supertriple Systems［J］.Communications in Algebra，2002，30(8):3825－3850.

［4］ Okubo S.Triple Products and Yang-Baxter Equation (Ⅱ):Orthogonal and Symplectic Ternary Systems［J］.J.math.phys.，1993，34(7):3292－3315.