基于混沌神经网络的液压集成块智能优化设计
2011-01-24宁建荣
于 玲, 宁建荣
(沈阳化工大学机械工程学院,辽宁沈阳110142)
由于液压集成块外部承装元件的多样性、元件外形的不规则性以及内部孔道网络的复杂性,使其设计工作异常困难而且极易出错.因此,液压集成块设计的核心问题就是其内部孔道和外部元件布局集成方案的自动优化设计,是在外形干涉和孔道连通校核支撑下的液压元件三维布局方案的自动寻优设计.这是一种具有性能约束的复杂的立体空间布局问题,数学上称之为组合最优化[1-2].
遗传算法、模拟退火算法、人工神经网络、混沌等人工智能方法为布局优化问题提供了新的思路和手段.遗传算法在求解NP-C类型的组合优化问题及非线性多目标函数优化问题方面有一定的优越性,但它存在“过早收敛”的缺陷,常常陷入局部最优解而不能自拔.模拟退火算法依据Metropolis准则,既可以接受优化解,又可以在一定范围内接受恶化解,具有跳出局部最优点的能力.但对于大中型问题,模拟退火算法的初始温度通常选取得很高,而且温度下降非常缓慢,大大增加了运算量,特别是对于带性能约束的布局问题,计算更加复杂费时[3].人工神经网络具有自适应性、自学习性、强容错行和巨并行性等许多人脑所具有的特性,自从Hopfield提出具有反馈神经网络模型并较成功地解决TSP问题以来,人们开始把神经网络应用于各种组合优化问题的求解过程中,同时为避免Hopfield网络陷入局部极小,许多具有混沌动力学特性的神经网络被提出来,为组合优化问题的全局寻优提供了新的手段[4].
由于布局设计问题的多样性、求解过程的综合性,单纯地应用一种算法来解决布局设计问题,往往难以取得满意的效果,将多种算法有效地结合起来形成有效的混合算法,再与人工智能有机结合就会产生解决液压集成块布局设计问题的有效方法[5].本文基于退火控制构造一种混沌神经网络模型,并将它引入到液压集成块布局布孔优化设计中,这种基于退火控制的混沌神经网络模型不但具有自组织特性,同时还具有克服陷入局部极小的能力.
1 基于退火控制的混沌神经网络模型及其优化机理
1.1 基于退火控制的混沌神经网络模型
通过在Hopfield神经网络的动态方程中加入一个负的自反馈项,将混沌机制引入Hopfield网络,同时结合模拟退火技术来控制混沌动态,构造如下的具有自组织特性和克服陷入局部极小能力的混沌神经网络模型:

其中,式(1)为网络动态方程,式(2)为神经元激励函数,式(3)和(4)类似模拟退火算法中的退温函数.vi(t)为第 i个神经元的输出; ui(t)为第i个神经元的内部状态;~ωij是第j个神经元到第i个神经元的连接权;Ii、I0分别为设定阈值和外加混沌量;β和λ分别为尺度和退温参数.
1.2 优化机制
为了研究上述模型的混沌搜索机理,以单个神经元(α=0)为例来检验该网络的动力学特性.
网络的参数和初值取值如下:

图1为单个神经元在取以上参数时网络的输出v(t)、退温函数z(t)和η(t)的时间演化图.从图1中可以看出:该网络具有混沌动力学行为,随着退温函数zi(t)的不断衰减,网络的动态特性经历了一个从奇异吸引子到稳定平衡点的连续逆分叉过程,然后逐渐收敛到稳定的平衡点.由于混沌具有的遍历性特性,使系统按自身的演化行为不重复地遍历所有可能状态,从而使网络避免陷入局部极小.当混沌动力学行为消失后,网络基本上由梯度下降的动力学控制,类似于Hopfield网络.由此可以看出:该混沌神经网络模型经历了基于混沌的“粗搜索”和基于HNN的“细搜索”.在粗搜索阶段,系统一开始就进入大范围意义下的较强混沌动态混沌搜索,随着混沌搜索的进行,控制参数开始退温,退温到一定程度,由系统的自组织能力,混沌动态退出,进入逆分岔阶段.此后,搜索过程将限制在一些周期解中,且能随控制参数的减小而进一步缩小搜索区域.当逆分岔现象随控制参数的进一步退温而达到周期形态时,算法得到一个全局意义下最优解的某一解,从而粗搜索过程结束.在细搜索阶段,随着粗搜索结束,系统中控制参数决定项的作用很弱,优化过程基本按能量函数的梯度下降方向进行.寻优过程将由粗搜索得到的解小范围内按HNN梯度下降机制进一步搜索,较快收敛到全局意义下较满意的解.

图1 输出v(t)、退温函数z(t)和η(t)的时间演化图Fig.1 Time evolution curves on output functions of v(t)、z(t)and η(t)
2 利用混沌神经网络进行集成块布局优化设计
液压集成块的布局布孔优化设计可以通过每个液压元件的安装面Fk、安装角度αk及其在安装面上的相对坐标(Xk,Yk)来表示.
2.1 安装面Fk
液压集成块的底平面为安装底面,不安装任何元件,所以,可以将n个液压元件分别布局到前、后、左、右、上5个面中,则网络可以使用5× n个神经元,并按5行n列排列.第1项为列约束,表示网络达到稳定状态时,每一列中只能有1个神经元输出为1,其余神经元输出为0,即每一个布局元件只能在某一确定的面上使用1次,此项为0;第2项为全局约束,表示所有神经元中输出值为1的神经元个数必须为n,确保仅使用n个待布局元件,此项也为0.根据上述布局目标,构造如下安装面能量函数:

式中,E1表示液压集成块安装面能量函数;vxi表示第x行i列的神经元输出;vyi表示第y行i列的神经元输出;n表示待布局的液压元件的个数; A1和B1为正的权值.
2.2 安装角度αk
每个待布局液压元件的安装角度一般为0°、90°、180°、270°,各元件的角度互相独立,互不相关.因此,可以使用4×n个神经元的网络,按4行n列排列.第1项为列约束,表示网络达到稳定状态时,每1列中只能有1个神经元输出为1,其余神经元输出为0,即每一个布局元件只能有1个安装角度,此项为0;第2项为全局约束,表示所有神经元中输出值为1的神经元个数必须为n,确保仅使用n个待布局元件,此项也为0.根据上述布局目标,构造如下安装角度能量函数:

式中,E2表示液压集成块安装角度能量函数;vxi表示第x行i列的神经元输出;vyi表示第y行i列的神经元输出;n表示待布局的液压元件的个数;A2和B2为正的权值.
2.3 相对坐标(Xk,Yk)
由于单线网布孔算法可以保证满足单线网的最少孔道设计、最短路径设计和极大极小设计要求,集成块总体优化的目标中就只剩下阀块体体积最小、所有连通线网总路径最短和所有连通线网工艺孔总数最少这3个目标,采用线性加权和法,将下面的目标函数式作为问题的评价函数:

式中,S—集成块体上布置的液压元件总数;
W—阀块体体积;
G—连通线网路径总长;
H—工艺孔总数;
λ1、λ2和λ3—W、G和H的权值.
根据总体目标函数定义如下的能量函数:

式中,E3表示液压集成块总体目标函数能量函数;A3为正的权值.
由式(5)、(6)和(8)3个能量函数可以得出液压集成块自动优化布局的总的能量函数:

当系统达到全局最优时,式(9)中的前两项为0,第3项的值即为整个求解过程的总体目标最优值.通过上述能量函数,结合混沌神经网络的求解,可以确定每个布局元件的安装面、安装角度及其在安装面上的相对坐标,从而完成液压集成块的自动布局布孔优化设计.
3 布孔优化设计
根据集成块内部孔道空间关系及孔道连通设计规律,在实时孔道干涉校核下,分别对单条线网内多个两端线网的连通顺序和多条线网之间的布线顺序进行优化,在保证所有孔道百分之百连通下完成全部孔道的最优化设计.
4 设计实例
为了验证上述算法的实用性,下面以某液压系统为例进行计算.系统原理如图2所示.模拟退火运算起始温度为5℃,温度衰减系数为0.9,目标函数中的体积、路径总长、工艺孔总数的权值分别取为0.000 01、0.01、1 000,这样可尽快消除含有禁忌的布局方案,并使得工艺孔总数最少.在输入连通关系和元件信息后,得到优化结果较优备选方案,见表1.从表1中可以得出优化结果:共有工艺孔12个,集成块的各边长分别为200 mm,220 mm,128 mm.根据优化设计结果,可画出孔道网络桁架结构图和集成块立体装配图(如图3所示)供设计人员参考.

图2 插装阀液压系统原理Fig.2 Schematic of cartridge valve system

表1 优化设计备选方案Table 1 Prepared schemes from optimal design
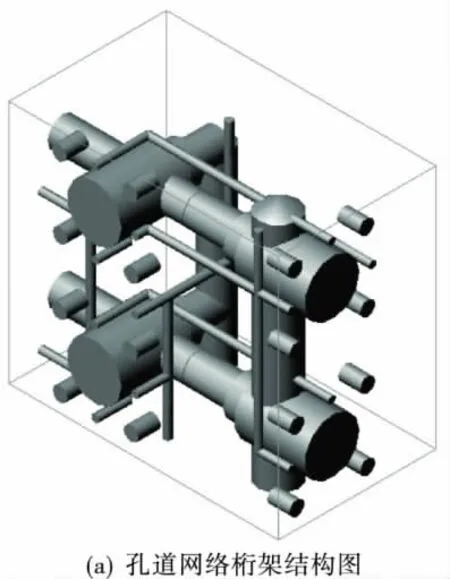

图3 插装阀集成块设计实例Fig.3 The design result of cartridge valve system
5 结论
液压集成块设计的核心问题是内部布孔和外部布局集成方案的组合优化问题.将基于退火的混沌神经网络技术应用到液压集成块设计中,成功解决了集成块布局布孔优化设计问题,并以工程设计实例验证了该系统的可行性和有效性.结果表明:基于退火控制的混沌神经网络模型在液压集成块自动布局优化设计上表现出较强的全局寻优能力,能快速、准确地生成集成块布局布孔优化方案,是寻找组合优化问题全局最优解的一种有效工具,为三维布局优化问题提供一个较好的前景.
[1] 李利.液压集成块智能优化设计理论与方法研究[D].大连:大连理工大学,2002:10-15.
[2] 冯毅,张宏,田树军,等.基于智能虚拟设计方法的液压集成块设计[J].计算机集成制造系统,2006,12(3):339-345.
[3] 王凌.智能优化算法及其应用[M].北京:清华大学出版社,2001:17-116.
[4] 李建勇,鄂明成,曹月东.利用混沌人工神经元网络进行布局优化设计计算[J].制造业自动化,2000,22(1):21-29.
[5] 毛亚林,张国忠,周明,等.一种改进混沌神经网络及其在组合优化问题中的应用[J].山东大学学报,2005,35(2):72-76.
