如何解决“绳”和“弹簧”的突变类问题

张强

(奎屯市第一高级中学 新疆 奎屯 833200)

在中学物理中“绳”和“弹簧”都是一种理想化的物理模型.以轻质“绳”和轻“弹簧”为载体，设置复杂的物理情境，考查力的概念、物体的平衡、牛顿定律的应用及能的转化与守恒，是历年来高考命题的重点，几乎每年高考试题均有所见.因此在高考复习中也引起了教师和学生的足够重视．

大多数学生对此类问题涉及的知识要点不能深化理解，思维不够灵活而导致容易出错．而一些缺少经验的教师通常又讲不透彻涉及的知识要点，无法引导学生用创新思维去灵活运用解决这类问题．下面笔者通过多年积累的一些经验，谈谈如何引导学生解决“绳”和“弹簧”的突变类问题．

首先要掌握“绳”和“弹簧”具有的基本特性.在中学物理中涉及到的“绳”和“弹簧”都是一种理想化的物理模型，都是轻质“绳”和轻“弹簧”，不计质量或者说质量和重力均可视为零.除此以外各自具有以下基本特性.

(1)对于“绳”来说，同一根绳的两端及其中间各点的张力大小相等，绳只能受拉力，不能承受压力(因绳能变弯曲)；绳对物体拉力的方向总是沿着绳指向绳收缩的方向，无论绳所受拉力多大，绳子的长度认为不变，即不考虑或忽略绳子的形变；若突然烧断(或剪断)绳的瞬间，绳子的拉力立即消失，即绳子中的张力可以突变．

(2)对于“弹簧”来说，同一弹簧的两端及其中间各点的弹力大小相等，弹簧既能承受拉力，也能承受压力(沿着弹簧的轴线)；由于弹簧受力时，发生形变需要一段时间，形变恢复也需要一段时间，在瞬间内形变量可以忽略；因此，在分析瞬时变化时，可以认为弹力大小不变，即弹簧的弹力不发生突变．

其次要灵活应用力与加速度的瞬时对应关系.由牛顿第二定律知，加速度是由合外力决定的，即有什么样的合外力就有什么样的加速度相对应．当合外力恒定时，加速度也恒定；合外力随时间变化时，加速度也随时间改变，且瞬时力决定瞬时加速度．可见，确定瞬时加速度的关键是正确确定瞬时作用力.因此“绳”和“弹簧”具有的基本特性的最后一点就是解决这类突变问题的关键．

下面通过几道由浅入深的例题来详细分析和讨论如何解决“绳”和“弹簧”的突变类问题．

【例题1】天花板上用细绳吊起一个质量为m的小球,小球保持静止，如图1(a)．当突然烧断(或剪断)细绳的瞬间，下面小球的加速度为多大？

图1

解析：以小球为研究对象，做烧断(或剪断)前和烧断(或剪断)时的受力分析.

剪断前小球保持静止，小球受两个力，拉力T、重力mg，如图1(b).有

T-mg= 0

剪断细绳的瞬间，绳子的拉力立即消失，小球只受一个力，重力mg，如图1(c)，有

mg=ma

解得a=g， 方向竖直向下.

【例题2】同时用细绳和轻质弹簧挂起一个质量为m的小球,小球保持静止，如图2(a)．当突然烧断(或剪断)细绳的瞬间，下面小球的加速度为多大？

解析：以小球为研究对象，做细绳烧断(或剪断)前和细绳烧断(或剪断)时的受力分析.

剪断前小球保持静止，小球受两个力，弹力F弹、重力mg，如受力图2(b).有

F弹-mg=0a=0

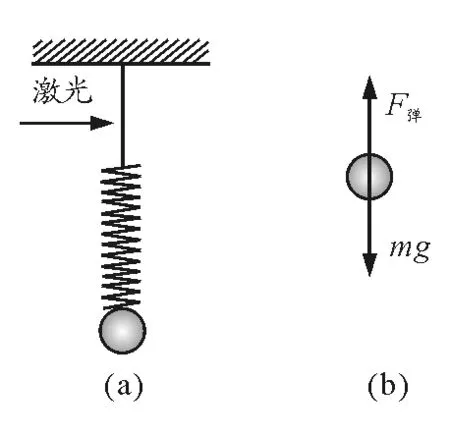
图2

剪断细绳的瞬间，绳子的拉力立即消失，但弹簧弹力大小不变，即弹簧的弹力不突变，小球仍受两个力，弹力F弹和重力mg，如图2(b).有

F弹-mg=0a=0

小球的瞬时加速度仍然为零.

【例题3】用轻质弹簧挂起一个质量为m的小球,小球保持静止，如图3(a).现用一束激光射向轻质弹簧，在烧断轻质弹簧的瞬间，下面小球的加速度为多大？

解析：以小球为研究对象，轻质弹簧突断前和轻质弹簧突断时的受力情况一样，如图3(b).

弹簧突断前

F弹-mg=0a=0

图3

由于同一弹簧的两端及其中间各点的弹力大小相等，弹簧突断时，两段弹簧的形变量都未来得及改变，弹簧弹力大小不变，即弹簧的弹力不突变，小球仍然满足

F弹-mg=0a=0

小球的瞬时加速度仍然为零.

对于用激光打弹簧或弹簧突断的问题，大多数学生包括教师都会产生疑虑：弹簧突断前整根弹簧对物体的弹力和弹簧突断瞬间下半段弹簧对物体的弹力能相等吗？弹簧突断瞬间毕竟变成两根不同的弹簧，弹簧的劲度系数发生改变，两根弹簧的形变量也不同，弹簧突断的瞬间下半段弹簧对物体的弹力还等于物体的重力吗？这个结论让学生一时无法接受.如果学生能接受和理解，这类弹簧突断的问题就非常简单了，甚至题目一出答案直接就看出来．那么如何在教学中 突破这个问题？下面笔者介绍一种创新性思维方法来突破这个问题．

方法：用打断后的两段弹簧通过轻绳串联等效替代即将打断的原弹簧(图4).用激光打断弹簧就相当于直接打断中间的轻绳．在打断前，两段弹簧的弹力相等都等于小球的重力.当打断轻绳的瞬间，绳子的拉力立即消失，但弹簧B对小球的弹力大小不变，弹簧的弹力不突变，小球仍受两个平衡力.有

F弹-mg= 0a=0

小球的瞬时加速度为零.

图4

今后再遇到弹簧突断的问题，就可以事先用打断后的两段弹簧通过轻绳的串联来等效替代即将打断的原弹簧，弹簧突断的问题就转化成了连接下半段弹簧的轻绳突断的问题，这个问题就又回到了例题2．用这种创新性思维的方法来突破这个问题使复杂的问题变得浅显易懂，学生也容易接受，更具有说服力．

【例题4】如图5(a)，天花板上用细绳连接A球后悬于O点，A、B两球由一轻弹簧相连保持静止，A、B两球质量都为m.如果将细绳烧断，则在绳断瞬间，两球的加速度分别为多大？如果将弹簧烧断瞬间，两球的加速度又分别为多大？

解析：以A、B两球分别为研究对象，做烧断前和烧断时的受力分析．

烧断前A、B静止，如图5(a);A球受三个力，拉力T、重力mg和弹力F弹，如图5(b)；B球受两个力，重力mg和F弹′，如图5(c)，取向上的方向为正.

A球T-mg-F弹=0

(1)

B球F弹′-mg=0

(2)

图5

由式(1)、(2)解得

T=2mgF弹=F弹′=mg

(1)将细绳烧断时，A球受两个力，因为绳的拉力T立即消失，而弹簧有形变，瞬间形变不改变，弹力还存在．如图5(d)，A球受重力mg、弹簧给的弹力F弹．同理，B球受重力mg和弹力F弹′．

A球 -mg-F弹=maA

(3)

B球F弹′-mg=maB

(4)

由式(3)解得aA=-2g(方向向下)

由式(4)解得aB=0

错解：细绳烧断时，以(A+B)为研究对象，系统只受重力，处于完全失重状态，所以加速度为g，则A、B球的加速度为g．出现上述错解的原因是研究对象的选择不正确.由于细绳烧断时，A球受力发生改变，B球受力不变，A、B球具有了不同的加速度，不能做为整体研究．

(2)将弹簧烧断瞬间，弹簧有形变，瞬间形变不改变，弹簧弹力大小不变．因此弹簧烧断瞬间A、B两球受力情况不变．由图5(b)，A球受三个力，拉力T、重力mg和弹力F弹；如图5(c)，B球受两个力，重力mg和F弹′．

A球T-mg-F弹=0

B球F弹′-mg=0

解得aA=0aB= 0

【例题5】如图6(a)所示，一质量为m的物体系于长度分别为L1、L2的两根细绳上，L1的一端悬挂在天花板上，与竖直方向夹角为θ，L2水平拉直，物体处于平衡状态．

(1)现将细绳L2剪断，求剪断时物体的瞬时加速度多大.

(2)若将图6(a)中的细绳L1改为长度相同、质量不计的轻弹簧，如图6(b)所示,其他条件不变.求剪断细绳L2时物体的瞬时加速度多大.

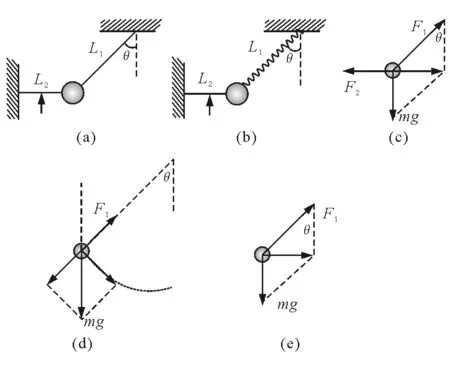
图6

解析：(1)如图6(a)，以质量为m的物体为研究对象，细绳L2剪断前受力情况如图6(c),物体受三个力,即细绳L1、L2的拉力分别为F1、F2和重力mg,物体处于平衡状态，此时满足

当细绳L2剪断瞬间，绳L2的拉力F2突然消失，绳L1上张力的大小发生了突变，物体在细绳L1的拉力F1、重力mg的作用下将沿弧线下摆，如图6(d).

此瞬间

F1=mgcosθ

F合=mgsinθ=ma

解得

a=gsinθ

(2)如图6(b)，当细绳L2剪断瞬间，绳L2的拉力F2突然消失，弹簧L1的形变量未来得及发生变化，弹力F1的大小和方向都不变，此时物体只受重力mg和弹力F1两个力，如图6(e)，物体所受的合力与F2等大反向.由牛顿第二定律得

F合=mgtanθ=ma

所以

a=gtanθ