数值模拟和集中参数分析法确定熔模铸造工艺凝固时间的对比分析

夏伯雄，杜 军，汪明玲，葛晓健，张 玲

（武汉软件工程职业学院机械制造工程系，湖北 武汉 430205）

熔模铸造对于生产净形零件是一个重要的生产过程。这个过程基本上是在一个预热陶瓷沙箱内凝固的。热分析是此系统设计的关键领域[1]。虽然凝固时间的估计是车间的第一手需求，然而当微观结构与散热路径密切相关时，热随时间的变化决定着产品的质量。热从熔模铸造铸型的转移受辐射和对流的双重控制。研究人员试图提出一次性模型来预测凝固时间，这是以简单的假设为基础的，如恒壁温。随着数字化计算机的问世和商业工程软件包的激增，在设计优化和原型开发的过程中，该行业已经成熟到能足以使用这样的代码。值得注意的是今天的模拟已达到了成熟的水平，造型既进行到了宏观尺寸，又扩展到了更精细的枝状水平[2]。这种战略尤其重要的是消除了铸件的缺陷。

从文献调查来看，全面计算流体动力学（CFD）和集中参数都曾经尝试过用于分析熔模铸造。然而，这两种方法从未比较过。设计师第一手的预测总是运用集中计算，这样可能导致误差。因此，在本文中，将全相能量数值计算法与集中参数公式法的求值进行了比较。为此，以一个圆柱形几何图形为对象考虑分析。铸型假设是充满了处于908 K时的A356合金，即20℃的过热。壁上的热传导既有对流又有辐射。对流换热系数取固定值5 W/m2K，这是对静态空气的合理估计。辐射部分的计算不妨以15元左右的人民币价值来描述。该材料性能列于表1。模具填充物的热效应被忽略，换句话说，已经在最初的过热质量要求中予以了考虑。

表1 材料特性

1 方法介绍

1.1 数值模拟方法

凝固过程由能量方程控制：

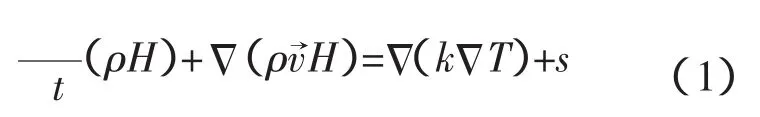
在这里，ρ为密度，H为焓，T是温度，t表示时间。等式右边的s项是一个原始项，当没有内热产生时其值为零。速度部分的影响可被忽略，当尺寸是几cm的中型铸件时，速度没有影响到铸件凝固前沿的热放出。

液体部分糊状区与其温度的关系如下：

对于 T＞Tliq，β=1；而当 T＜Tsol时，β=0

Tliq为液相线温度；Tsol为固相线温度。

液体部分非线性方程也有报道，公式固然接近于物理学。然而，Bakhtiyarov等[3]表明，对于不同类型的方程，如Sceil模型，铝合金等不会有太多的液体方程的变化，建议在工程实践中可直接采用线性规律。

能量方程是一个线性方程，当适当的边界条件已知时可进行数值求解。边界条件可能是Dirrichlet型或Neumann型或它们的组合。在Dirrichlet型中，可提供温度值。在Neumann型中，可使用热通量值。绝热，即绝缘边界是其中特殊的一类，热通量为零。

焓的定格法是建模凝固非常流行的一个方法，这要归因于Voller和Prakash[4]。这种方法不是将液体和固体区域进行分开处理，而是将液体和固体区域当成一个共同的网格用于整个区域。作为焓方程的部分解法是跟踪凝固前沿。糊状区的液体部分可从方程（2）描述的线性关系中得到。使用上述方程是要建立一个模型来运用FLUENT商业CFD代码[5]。流体体积的方法已被用于捕捉边界[6]。

边界条件是：

在坐标轴上：偏导数趋进于零，即 U/ri和T/ri=0，其中ri指坐标，U和T分别为速度和焓场。

在铸型壁上：传导热系数值h是已知的。铸型壁的传热率由q=-h（Tw-Tamb）给出，其中T为铸型壁温度；Tamb为环境温度。

1.2 集中参数分析法

Upadhya等人[7]提出的集中分析法，可以用以下方式进行。铸造的热传导率由下式给出：

其中h是传热系数，A为表面积，Ts和T∞分别是外壳和周围环境的温度。

如果L*是金属溶融的有效热，总凝固过程的传热时间为tsol，则总传导热量为：

其中，ρ为密度，V为体积。

其中，L是潜热，ΔTsuper是过热度。

凝固所需时间：

我们将物体的模数定义为体积与面积的比率，即M=V/A。模数值低就表示物体相对体积具有较高的表面积。因此，模数接近零，标志着物体具有很高的表面面积。

现在可以看出：

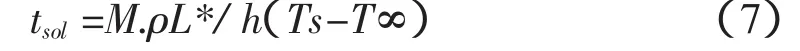
因此，我们观察到凝固时间与模数成正比。

热传导包括辐射和对流。热传导系数的辐射部分可从Stephan-Boltzmann辐射方程获得，给出如下：

对流部分可以用不同的方式加以分析。一个简单的方法是建议取 hconv=c（Ts-T∞）1/3，其中 c 是一个依表面几何形状而定的常数，hrad为辐身传热系数；hconv为对流传热系数。另一种方法是，以表面的方向性为基础来选择自然对流的相关性，见参考文献[8]。然而，对于目前的计算，我们使用了以前讨论过的hconv固定值。

2 分析与讨论

模拟是在模数M的几个不同层次上进行的。包括使用了以前所提到的约10000个节点的轴对称方程。通过比较三种格层次的结果来确保格的独立性。格独立凝固时间的推导值与目前网格配置的计算值相差仅约0.5%。

控制传导方程可利用已经提及的商业CFD求解器FLUENT进行数值求解。方程式基本上整理成以下形式，以利于用一种标准形式进行方程的离散化：

按照SIMPLE算法运用以压力为基础的有限体积法使方程离散化[9]。其中φ表示任何守恒的变量，S是原始边界。在计算流体力学（CFD）过程中，上述类型的微分方程可转换成一个由数字计算机解决的代数方程。对于控制方程的解法，规定了一个带有1×10-7偏差的收敛判断准则。作为离散处理，使用了具有较高准确性级别输出的二阶展开方法。详细数值实施过程可参见[5]，对模具进行注射成形工艺的填充工作过程可参见[10]。

通过监测最内侧的液体部分的凝固端点，可估算出凝固时间。

如果已知物体的模数，运用方程（2）也可估计出凝固时间。在这里应当指出的是，Upadhya等没有以物体对象作为整体来确定模数[7]，而是将物体对象离散成若干个小体积，显然这样做会更好地预测凝固时间。在[7]中提到的这个方案称为节模数方法，并发现这种方法在精度和计算资源方面非常具有竞争性[11]。

图1显示了模数为0.0125的物体对象的温度随时间变化的曲线。这个M值对应一个长度为5.0cm，直径10.0cm的圆柱体。从图1可观察到，最初有一个平缓区，这说明过热材料的冷却约21 s。一旦凝固开始，潜热释放到环境。液体部分随着时间逐渐减少，直到凝固停止在固相线的温度。

现在定义一个术语Tr，Tr是通过全相的分析获得的凝固时间与集中参数公式法预测的凝固时间的比率。Tr将随着材料内较大梯度的大体积的模数增加而变化。

这可从图2中观察到，时间比Tr随着模数增加的二次方而增加。Tr的表达式为：

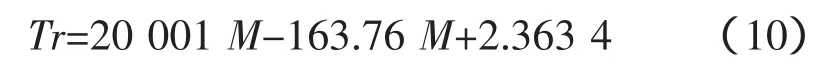
从以上函数中可以看出，当模数为零时，Tr=2.36。极限值零模数对应于非常高的表面积情形。零模数的极限情况是研究人员特别感兴趣的，因为它涉及到的能源的最高可能传导区域。

图1 液体部分随时间的变化（M=0.0125）

图2 模数对凝固时间的影响

3 总 结

本文表明，可以从能量方程的完整解法得到的凝固时间和集中分析法得到的凝固时间之间建立的一个函数关系。这样的函数关系一旦建立，可以通过计算对一定模数物体的凝固时间做出快速的预测。分析还表明，对于模数接近零值的高表面体积比，实际凝固时间大约为集中分析法预测时间的2.36倍。一般认为是低模数高价值的小件物品如黄金饰品往往走熔模铸造的生产路线。

［1］G.H.Geiger.and D.R.Poirier.Transport Phenomena in Metallurgy［J］.Addesson Wesley，1980.

［2］Hamilton RW，See D，Butler S et al.Multiscalemodeling for the prediction of casting defects in investment castaluminum alloys［J］.Mater Sci Eng，2003，A 343：290-300.

［3］Bakhtiyarov SI，Overfet RA，Teodorescu SG.Fractionalsolid measurements of solidifying melt［J］.J Fluids Eng 2004，126:193-197.

［4］Voller VR，Prakash C.A fixed-grid numerical modelingmethodology for convection-diffusion mushy region phase-change problems［J］.Int J Heat Mass Transfer 1987，30：1709-1720.

［5］Fluent Inc.FLUENT Users Manual[M].Lebanon，2004.

［6］Hirt W，Nichols BD.method for thedynamics of free boundaries［J］.J Comput Phys，1981，39：202-225.

［7］Upadhya GK，Das S，Chandra U et al.Modeling theinvestment casting process：a novel approach for view factorcalculations and defect prediction［J］.Appl Math Model，1995，19：354-362.

［8］Bejan A.Convective heat transfer[M].Wiley,New Jersey，2004.

［9］Patankar SV.Numerical heat transfer and fluid flow［J］.Hemisphere Publication，Washington，1980.

［10］Samanta SK，Chattopadhyay H，Godkhindi MM et al.A numerical study of solidification inpowder injection molding process［J］.Int J Heat Mass Transfer，2008，5：672-682.

［11］Kotschi R，Plutshak L.An easy and inexpensive techniqueto study solidification of castings in three dimensions ［J］.AFS Trans，1981，89：601-608.