碳纳米管增强复合材料的界面破坏形态及改善措施

罗冬梅,朱文亮

(1.佛山科学技术学院土木与建筑工程系,广东佛山,528000;2.华南理工大学土木工程系,广东广州,510641)

自1991年Iijima[1]发现碳纳米管(carbon nano-tubes,CN Ts)以来,碳纳米管增强复合材料一直受到广泛关注,很多学者用不同的方法研究碳纳米管增强复合材料的力学性能。Chen等[2]从碳纳米管复合材料中取出一个代表性体积胞元,用有限元方法计算复合材料的有效弹性模量。罗冬梅等[3]用双尺度均值化法和多相Mori-Tanaka法计算了界面碳纳米增强复合材料中界面层特性对复合材料整体力学性能的影响。Fisher等[4]用有限元方法研究碳纳米管弯曲对复合材料性能的影响。Gao等[5]将碳纳米管视为纤维,用剪滞模型研究碳纳米管增强复合材料的性质。Odegard等[6]利用分子结构力学模型将碳纳米管简化为等效连续纤维,用细观力学方法建立碳纳米管增强聚合物复合材料的本构关系等。目前,大多数研究针对的是碳纳米管增强复合材料整体的有效弹性模量及强度,对复合材料局部破坏特征的研究却很少。

本文利用文献[7]中推导的均质化理论和精确的周期性边界条件,计算包含界面相的非贯穿二维连续碳纳米管增强复合材料的整体弹性模量,并与文献[8]进行比较,以证明二维平面模型计算的可行性。考虑基体材料的非线性,对复合材料施加沿长度方向的边界位移,考察碳纳米管增强复合材料出现塑性变形或破坏的部位,进一步分析界面层特性对复合材料塑性变形及破坏的影响,通过对破坏端部的局部处理,探索性地提出两种改善碳纳米管复合材料破坏形态的方法。

1 二维平面模型模拟碳纳米管增强复合材料的力学性能

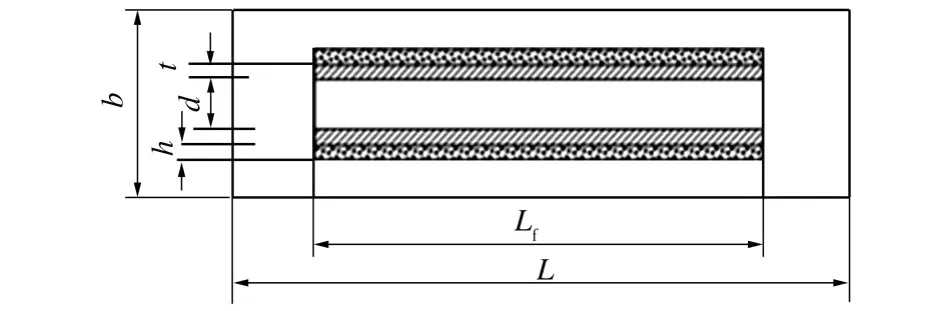
图1 碳纳米管增强复合材料平面模型Fig.1 Planar model of carbon nano-tube reinforced composites

文献[8]建立了包含界面相的三维非贯穿连续碳纳米管圆筒增强复合材料实体模型,用纳微观均质化法计算了复合材料整体有效弹性模量,并与经典Halpin-Tsai、Mo ri-Tanaka方法进行了比较,发现几种方法所得结果相当吻合。考虑到在三维实体模型中处理界面破坏问题的复杂性及计算时间的浪费,本文首先采用文献[7]中的均值化法基于二维平面模型计算碳纳米管增强复合材料的力学性能,并与三维实体模型计算结果进行比较。碳纳米管增强复合材料的平面模型如图1所示,其中,L=200 nm,Lf=100 nm,b=50 nm,d=14.66 nm,t=0.34 nm,h=6 nm。平面模型的典型有限元网格划分(取平面模型面积的1/4)如图2所示。

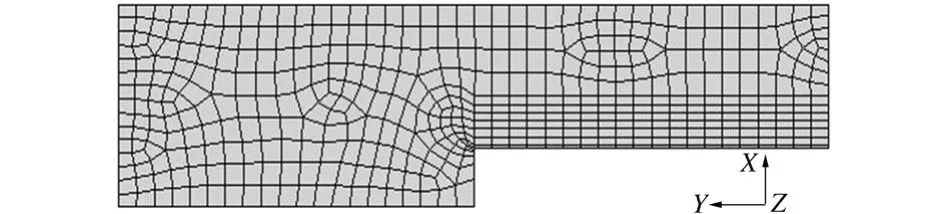
图2 平面模型的有限元网格Fig.2 FEM mesh of planar model

界面层体积比对复合材料弹性模量的影响如图3所示,界面层弹性模量对复合材料弹性模量的影响如图4所示。从图3和图4中可以看出,平面模型模拟结果的变化趋势与其他3种方法一致。由于二维平面模型忽略了碳纳米管的空间管状特性,平面情况下的单元网格划分和处理较为粗化简单,其结果更接近于基于平均法计算有效力学性能的经典Halpin-Tsai和Mori-Tanaka法,而较三维模型计算结果偏高,但最大误差不超过16%,且二者的差距比较稳定,可以通过网格的局部细化处理来提高计算精度。因此,用简单的二维平面模型模拟碳纳米管复合材料的力学性能以简化计算是可行的。

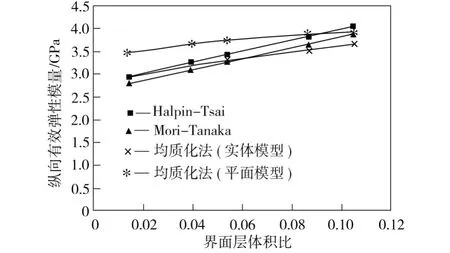
图3 界面层体积比对复合材料弹性模量的影响Fig.3 Effect of volume fraction for interface on effectiveelastic modulus of nano-composites

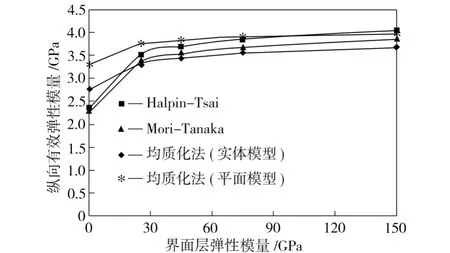
图4 界面层弹性模量对复合材料弹性模量的影响Fig.4 Effect of elastic modulus for interface on effective elastic modulus of nano-composites

2 界面层对碳纳米管增强复合材料破坏形态的影响

2.1 碳纳米管增强复合材料的破坏形式及部位

设碳纳米管纤维及界面层为线弹性材料,基体采用双线性随动强化非线性模型,主要材料性质如表1所示。边界条件为:在复合材料两端施加拉伸位移使其伸长率ε达到5%,ε=(su+sd)/Lm,其中(su+sd)为两端施加的拉伸位移之和,Lm为复合材料总长度。

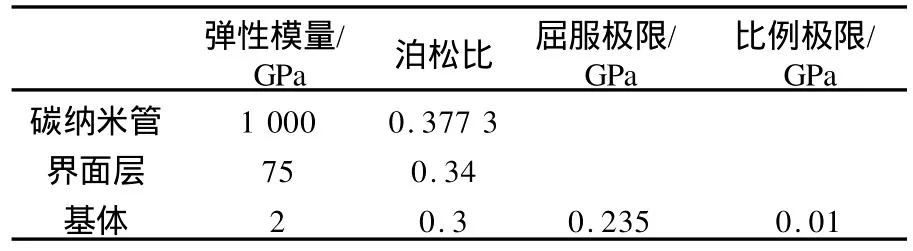
表1 材料性质[8]Table 1 Properties of thematerials

图5为碳纳米管复合材料等效塑性应变图,由图5可见,塑性变形发生在纤维端部与基体接触的界面处,其应力集中因子为

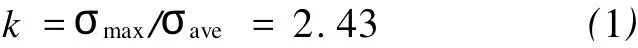
式中:σmax为塑性区最大应力;σave为离塑性区较远处的平均应力。基体与纤维粘结处的正应力与剪应力之比为8.746 4,正应力远大于剪应力,由此可见,纤维与界面结合端部的应力集中是导致碳纳米管增强复合材料破坏的主要原因。

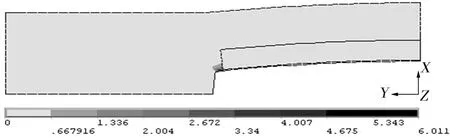
图5 等效塑性应变云图Fig.5 Distribution of effective plastic strain

2.2 界面层特性对碳纳米管增强复合材料破坏区应力的影响

分别取5组不同的界面层厚度(界面层弹性模量均为75 GPa)和5组不同的界面层弹性模量(界面层厚度均为6 nm),计算不同条件下在Y方向拉伸荷载作用下破坏区正应力的变化情况。图6所示为界面层弹性模量变化时,破坏区正应力随复合材料伸长率的变化情况。图6中每条曲线的第一个波峰点所对应的伸长率即复合材料刚出现塑性变形时的伸长率。随着界面层弹性模量的增大,波峰点对应的伸长率也在增大,界面层弹性模量增大到一定程度时(E>40 GPa),第一个波峰点所对应的伸长率几乎相同,只是正应力值随界面层弹性模量的增大而逐渐降低。图7所示为界面层体积比变化时,破坏区正应力与复合材料伸长率的关系。图7中各曲线第一个波峰点的意义与图6中的相同。从图7中可以看出,随着界面层体积比的增大,第一个波峰点所对应的伸长率逐渐增大,但最大正应力变化不大。由此可见,随着界面层弹性模量及体积比的增大,能够通过降低正应力或增大伸长率来延缓复合材料的破坏,但由于界面层特性变化不能改变结合端部的截面突变现象,端部应力集中无法消除,因而材料在结合端部的塑性破坏仍然不可避免。

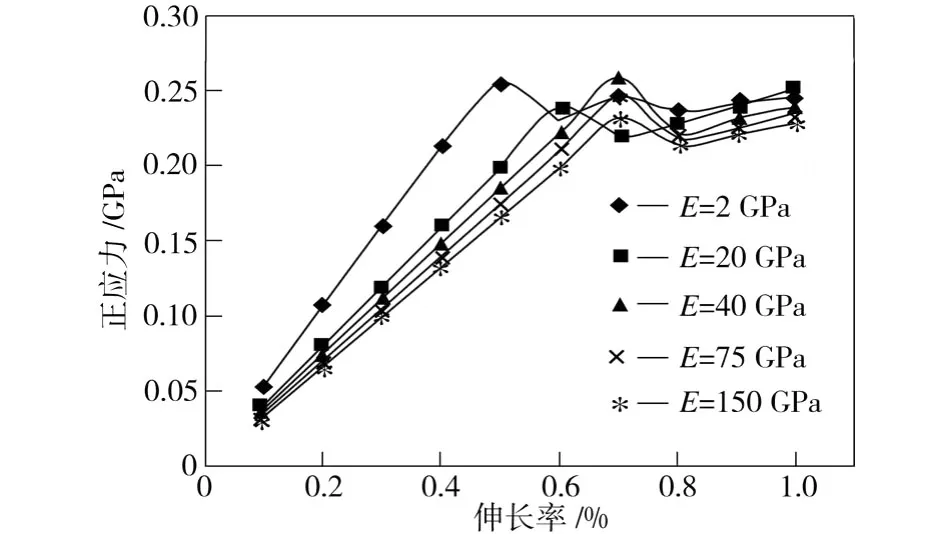
图6 界面层弹性模量对正应力的的影响Fig.6 Effect of Young’s modulus for interface on the normal stress

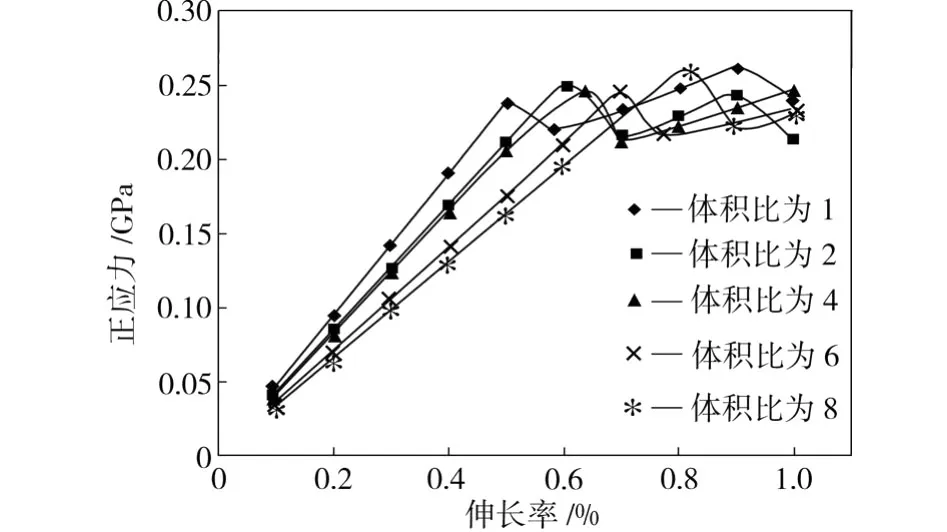
图7 界面层体积比对正应力的影响Fig.7 Effect of volume fraction for in ter face on the normal stress

3 改善碳纳米管增强复合材料破坏形态的两种方法

碳纳米管增强复合材料端部的应力集中是材料产生塑性变形的主要原因,针对这个现象,本文探索性地提出两种改善其破坏形态的方法。

3.1 改变纤维及界面层端部与基体的界面特性

3.1.1 内聚力模型

内聚力实质上是物质原子或分子之间的相互作用力,基于这种相互作用力与相对位移间的对应关系,周储伟等[9]推导了一种模拟复合材料界面的模型即内聚力模型,在模型中引入软化界面以取代与实际不相符的理想刚性界面。本文通过内聚力模型指数形式的表面势能得到内聚力界面单元界面应力(牵引力T)、界面相对位移(分离距离δ)、界面最大正牵引力σmax、最大正牵引力作用下的法向界面距离以及最大剪牵引力作用下的切向界面距的关系,以此描述界面的本构关系。

对于界面单元,界面的分离距离为界面的跳跃距离,即上、下界面的距离增量:

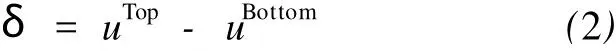
式(2)中的界面分离距离定义在如图8所示的局部坐标系中,可沿局部坐标中界面的法线方向n和切线方向t分解为

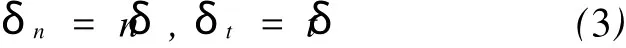
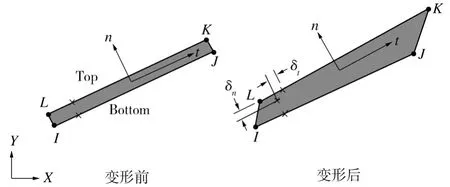
图8 界面单元原理图Fig.8 Schematic of Interface Elements

Xu等[10]提出了内聚力模型指数形式的表面势能:

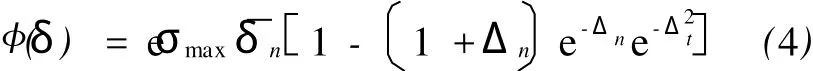
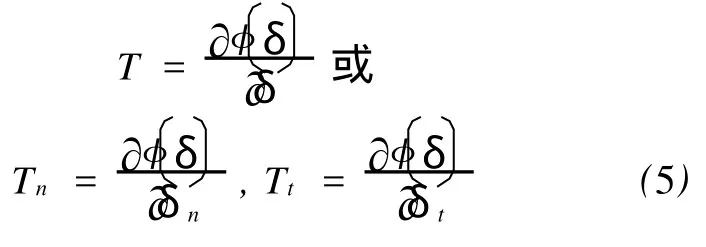
根据式(4)和式(5),得到正牵引力与剪牵引力为:

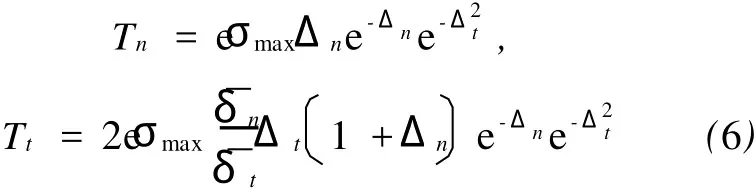
3.1.2 纤维及界面层端部与基体连接处的内聚力模型

在复合材料破坏形态的分析模型中,纤维及界面层端部与基体连接的界面被假设是理想刚性的,因而应力集中现象较为严重。为了真实反映界面特性对复合材料宏微观力学性能的影响,在纤维及界面层端部与基体连接处引入内聚力模型。

在纤维及界面层端部与基体连接处设置一个呈二次线性的内聚力界面单元,如图9中黑色部分所示。这种界面单元有6个节点,每个节点各有2个自由度,如图10所示。界面单元的初始厚度可以为0,即节点I和L、J和K、M和O是连结在一起的,这为模拟界面表面及界面间的分离过程带来了便利,初始连结在一起的2个节点的分离代表界面间的分离过程。

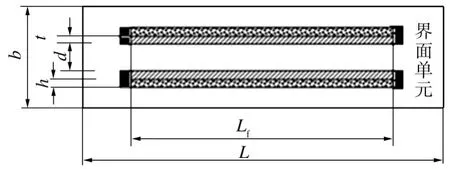
图9 设置内聚力界面单元的平面模型Fig.9 Planar model with cohesive interface element

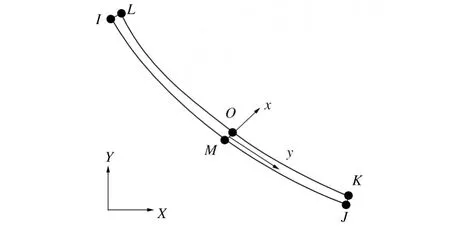
图10 二次线性单元Fig.10 6-node quadratic interface element

取两组模型来比较复合材料整体力学性能的变化。第一组模型为常规模型,第二组模型包含内聚力界面单元,称为内聚力模型。设界面单元初始厚度为0,界面单元的概念力学参数设为:最大界面正牵引力σmax=0.26 GPa,最大界面正牵引力所对应的正界面距离δn=2 nm,最大切界面距离δt=2 nm。设两组模型的几何尺寸相同,单元长度均为200 nm,各组分材料特性均按表1取值。

沿两组模型的Y方向逐渐施加位移,直到模型出现塑性变形为止。第一组模型出现塑性变形时的等效塑性应变云图参见图5,第二组模型的等效塑性应变云图如图11所示。对比图5和图11可见,两组模型发生塑性变形的位置有所变化。另外,内聚力模型刚出现塑性变形时的伸长率为2.4%,是常规模型对应值(0.77%)的3.1倍。内聚力模型通过内聚摩擦力消耗一定的断裂能,延缓了塑性应变的出现,提高了复合材料的整体力学性能

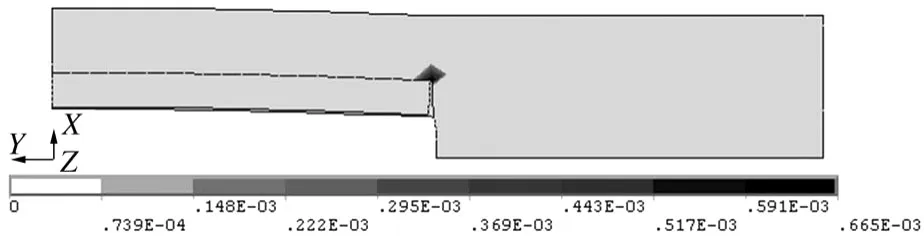
图11 内聚力模型的等效塑性应变云图Fig.11 Distribution of effective plastic strain of cohesive zonemodel

3.2 封闭碳纳米管和界面层

该措施通过封闭碳纳米管及界面层以达到提高复合材料的抗塑性变形的能力,如图12所示。封闭型模型的参数设为L=200 nm,Lf=80 nm,b=50 nm,d=14.66 nm,t=0.34 nm,h=6 nm,其1/4平面模型的有限元网格如图13所示。沿模型的Y方向施加拉伸位移直到碳纳米管增强复合材料出现塑性变形,此时其等效塑性应变云图如图14所示。由图14可见,复合材料塑性变形主要发生在界面与基体的接触面方向。在其他条件相同的情况下,封闭型碳纳米管增强复合材料刚出现塑性变形时的伸长率为4.5%,是常规模型的5.8倍,是内聚力模型的1.88倍,由此可见,封闭型碳纳米管改善了复合材料的应力集中现象,可更有效地延缓塑性变形的出现。

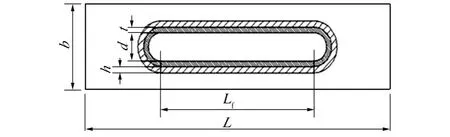
图12 封闭型平面模型Fig.12 Capped planar model

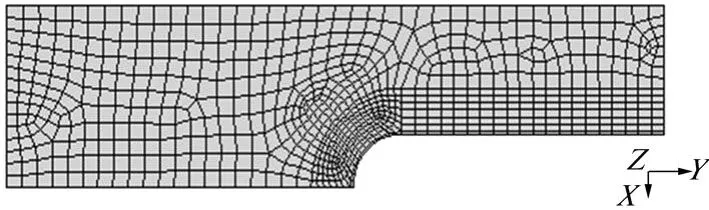
图13 封闭型模型的网格划分Fig.13 FEM mesh of capped planar model

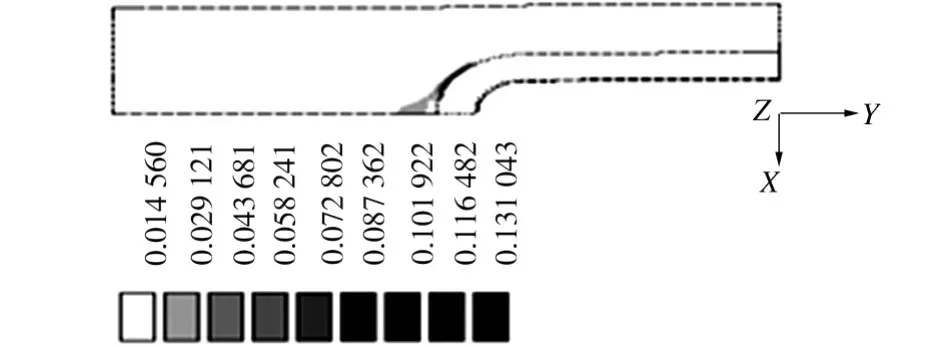
图14 封闭型模型的等效塑性应变云图Fig.14 Distribution of effective plastic strain of capped planar model

4 结论

(1)在拉伸载荷作用下,碳纳米管增强复合材料发生破坏的部位为碳纳米管及界面层端部与基体的连接处,应力集中是导致破坏的主要原因。

(2)随着界面层弹性模量及界面层体积比的增大,通过降低最大正应力、增大塑性伸长率,能够在一定程度上延缓复合材料的破坏,但不能改变界面结合端部应力集中的破坏本质。

(3)内聚力模型为模拟复合材料的真实界面提供了一种有效、便利的方法。

(4)封闭碳纳米管和界面层对延缓碳纳米管增强复合材料的塑性变形具有明显效果。

[1] Iijima S.Helical microtubules of graphitic carbon[J].Nature,1991,354:56-58.

[2] Chen X L,Liu Y J.Square representative volume elements for evaluating the effective material properties of carbon nano-tube-based composites[J].Computational Materials Science,2004,29:1-11.

[3] 罗冬梅,吴莹,黄健,等.纳米碳管增强复合材料界面特性对力学性能影响的数值分析[J].武汉科技大学学报,2009,32(3):279-283.

[4] Fisher F T,B radshaw R D,Brinson L C.Fiber waviness in nano tube-reinforced polymer composites-I:modulus predictions using effective nanotube properties[J].Composites Science and Technology,2003,63:1 689-1 703.

[5] Gao X L,Li K.A shear-lag model fo r carbon nanotube-rein forced polymer composites[J].International Journal of Solids and Structures,2005,42:1 649-1 667.

[6] Odegard GM,Gatesb T S,Wisea K E,et al.Constitutive modeling of nano-tube-reinforced polymer composites[J].Composites Science and Technology,2003,63:1 671-1 687.

[7] Luo D M,Wang W X,Takao Y.Application of homogenization method on the evaluation and analysis of the effective stiffness for noncontinuous carbon nanotube/polymer composites[J].Polymer Composites,2007,28(5):688-695.

[8] 罗冬梅,朱文亮,杨虹,等,界面特性对非贯穿连续碳纳米筒体增强复合材料力学性能的影响[J].机械强度,2011,33(3):396-402.

[9] 周储伟,杨卫,方岱宁.内聚力界面单元与复合材料的界面损伤分析[J].力学学报,1999,31(3):372-376.

[10] Xu X P,Needleman A.Numerical simulations of fast crack grow th in brittle solid[J].Journal of the Mechanics and Physics of Solids,1994,42:1 397-1 434.