特低渗透储层产量递减规律物理模拟实验＊

薛成国 杨正明 刘学伟 徐 轩 齐亚东 王名春

(1.中国科学院渗流流体力学研究所; 2.中国石油勘探开发研究院廊坊分院; 3.中海油研究总院)

随着特低渗透油藏的不断开发,对特低渗透油藏产量递减规律的分析与预测也变得越来越重要。与中、高渗透储层相比,特低渗透储层最明显的特点是具有启动压力梯度,其对特低渗透储层的产量递减规律具有不可忽略的影响[1-2]。近年来,一些学者开展了关于特低渗透储层产量递减规律的理论研究[3-5],但目前还未见有通过物理模拟实验进行研究的报道。笔者采用四川特低渗透砂岩露头岩样进行特低渗透储层产量递减规律物理模拟实验研究,以期为分析、预测特低渗透储层产量递减规律提供实验基础。

1 实验方法

选用取自四川某天然砂岩露头岩样制作二维平板模型用以模拟,结合吉林某油田实际生产情况,应用量纲分析方法确定实验所需的各项动态参数(如平板模型的尺寸,实验的初始压力、生产时间等),以确保实验可以较为真实、准确地反映实际生产情况。

1.1 平板模型制作

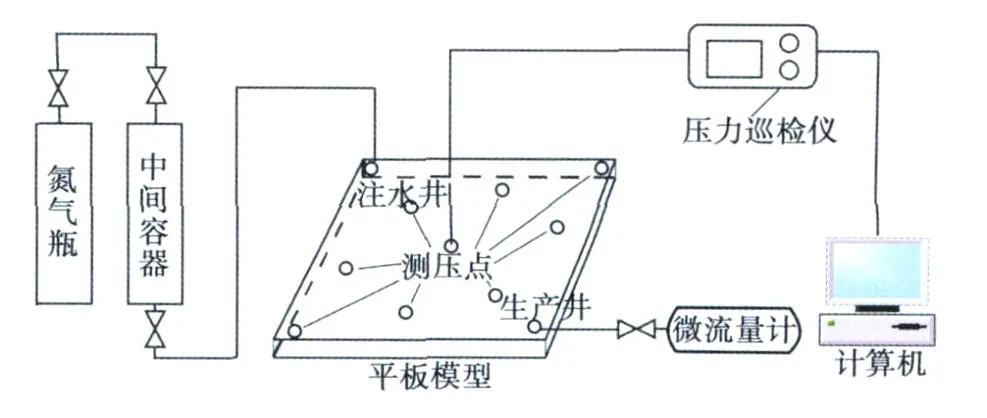
图1 特低渗透平板模型产量递减规律物理模拟实验流程

将取自天然露头的岩样首先加工成尺寸为40 cm×40 cm×30 cm的砂岩平板(共4块),沿对角线在平板两角钻取深孔模拟注采井(本次实验模拟五点法井网的1/4单元),在注采井主流线上及其两侧钻取表层浅孔(降低钻孔对平板模型流场的影响)布置测压点,注采井及测压点的分布如图1所示。烘干平板模型,将连接压力传感器的接头置于钻孔内并用胶固定,最后用按照一定比例混合的环氧树脂和固化剂进行模型的整体浇铸。待封胶固结后,将模型抽真空,在常压下对平板模型进行地层水初步饱和,之后用驱替泵向模型中注入地层水,将泵压稳定在0.5 MPa保持24 h,最后将模型静止放置48 h,以使其充分均匀地饱和地层水。该模型与人工填砂模型[6]相比,可以更真实地模拟特低渗透储层特征。

1.2 平板模型物性参数获取

从每块制作二维模型的岩样的边缘处分别钻取8块(水平、垂直方向各4块)小岩心进行气测渗透率测量,并计算出每块平板模型的平均气测渗透率;选择具有代表性的小岩心进行非线性渗流测试实验[7],得到每块平板模型的启动压力梯度。4个平板模型的物性参数见表1。从表1可以看出,M 0模型不存在启动压力,M 1、M 2、M 3模型均具有启动压力梯度,并且启动压力梯度随渗透率的减小而增大。

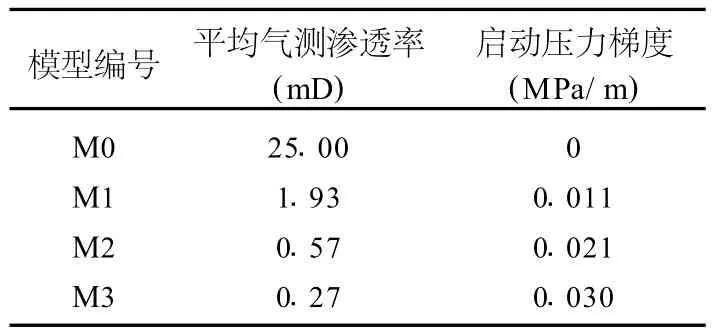
表1 4块平板模型的物性参数

1.3 实验流程

实验流程见图1。实验时,在常温下选用高精度的定压装置将平板模型的压力升高至0.1MPa,然后进行衰竭式生产实验。在测压点处连接高精度压力传感器,用压力巡检仪监测压力传感器的压力变化,设定每隔一定时间采集一次压力数据,并将信号传输给计算机,实现压力数据的自动采集;在采出井处用微流量计每隔一段时间人工采集流体流量。

2 实验结果分析与讨论

2.1 实验结果分析

图2和图3分别为模型生产井的无因次产量及模型压力随生产时间的变化曲线,其中无因次产量为生产井的瞬时产量与初始产量的比值。

根据阿普斯(A rps)产量递减模型[8],油气田的产量递减公式为

式(1)中:qi为初始时刻的产量,104t/a;Di为初始产量递减率,h-1;b为递减指数,无量纲常数。

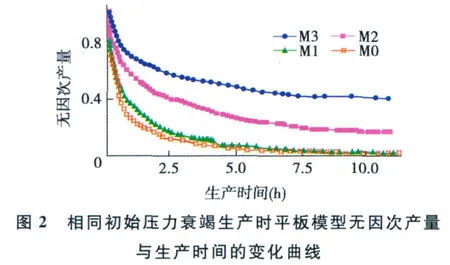
根据试凑法[9],利用式(1)对实验结果进行拟合,得到各个平板模型进行衰竭生产的初始产量、初始递减率和累积产量(表2)。

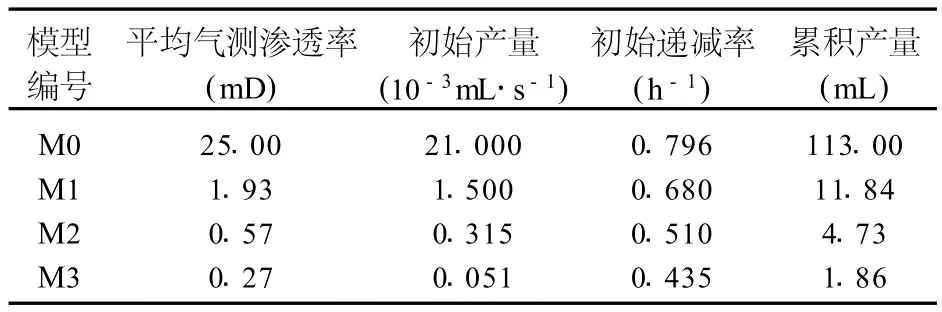
表2 相同初始压力衰竭生产时平板模型产量递减参数

据表2、图2、图3分析可知,平板模型渗透率越低,初始产量、初始递减率、累积产量越小,模型压力及生产井产量下降的速度越慢。

2.2 实验结果讨论

由表1可知,模型的渗透率越低,模型的启动压力梯度越大。启动压力梯度实际上是流体在特低渗透地层中的渗流阻力,而地层中真正用于生产的能量是在克服掉启动压力梯度后剩余的地层能量。因此,启动压力的存在降低了地层的初始产量、产量递减速度以及累积产量,也降低了地层能量亏空及地层压力下降的速度。徐运亭等[10]定义了特低渗透油藏有效驱动因子的概念,由其物理意义,特低渗透储层产量递减时的递减参数与有效驱动因子有着密切的关系。

注采井间建立有效注采系统时,由于启动压力梯度的存在而消耗的驱替压差(Δp消耗)为[11-12]

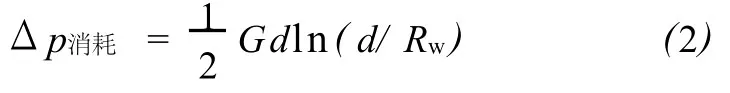
因此,特低渗透平板模型的有效驱动因子(E)为

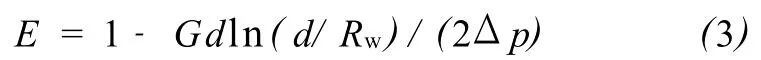
式(3)中:Δp为注采压差,M Pa;G为启动压力梯度,M Pa·m-1;d为注采井距,m;Rw为注采井半径,m。

根据式(3)可以计算得到各个平板模型在0.1 M Pa压力下进行衰竭生产时初始时刻的有效驱动因子分别为 1.00(M 0)、0.83(M 1)、0.67(M 2)、0.53(M 3)。平板模型初始递减率与有效驱动因子的关系如图4所示。

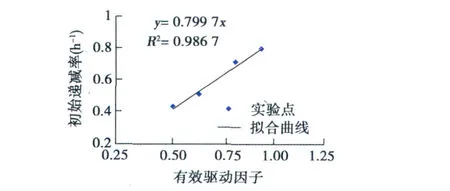
图4 平板模型初始递减率与有效驱动因子关系曲线

由图4可以看出,初始递减率与有效驱动因子之间有着较好的线性关系,其斜率大小(为0.799)与M 0模型(启动压力梯度为零的储层)的初始递减率(为0.796)基本吻合。因此,特低渗透储层的初始递减率与有效驱动因子具有以下关系:

式(4)中:D′i、Di分别为特低渗透储层和常规储层产量初始递减率,h-1;E为有效驱动因子。

因此,在低渗透储层(尤其是特低渗透储层)的产量递减分析时,必须考虑启动压力梯度的影响。

3 结论

(1)本文建立了进行特低渗透储层产量递减规律实验的方法,为特低渗透油藏产量递减规律的研究提供了一种新的思路和方法,通过本文方法封装的物理模型能够更真实地模拟特低渗透储层特征。

(2)对于特低渗透储层,在储层初始压力相同的情况下进行衰竭式开采时,渗透率越低,储层压力下降的速度越慢,储层的初始产量、初始递减率和累积产量也越小,这是由于储层渗透率低,启动压力梯度较大,储层内部流体流动阻力较大造成的。

(3)特低渗透储层产量递减规律与特低渗透油藏有效驱动因子有着密切的关系,因此,在低渗透储层(尤其是特低渗透储层)的产量递减分析时,必须考虑启动压力梯度的影响。

[1] 姜瑞忠,张晓亮,马江平,等.特低渗透油藏弹性采收率计算新方法[J].中国海上油气,2010,22(1):27-29.

[2] 黄延章.低渗透油层非线性渗流特征[J].特种油气藏,1997,4(1):9-14.

[3] 刘义坤,孙娜,文华.大庆外围低渗透油田产量递减分形特征及预测[J].油气地质与采收率,2008,15(6):80-82.

[4] 邓玉珍.异常高压特低渗透油藏产量递减规律预测方法[J].油气地质与采收率,2009,16(6):84-87.

[5] 杨正明,刘先贵,孙长艳,等.低渗透油藏产量递减规律及水驱特征曲线[J].石油勘探与开发,2000,27(3):55-56.

[6] 秦积舜,李久娣,孟红霞.平面物理模型的拟相渗规律研究[J].重庆大学学报:自然科学版,2000,23(增):111-113.

[7] 刘志远,杨正明,刘学伟,等.低渗透油藏非线性渗流实验研究[J].科技导报,2009,27(17):57-60.

[8] 姜汉桥,姚军,姜瑞忠.油藏工厂原理与方法[M].东营:中国石油大学出版社,2006:247-250.

[9] 王金多,刘国静,秦凯峰,等.产量自然递减类型的综合判断及构成分析[J].断块油气田,2007,14(2):44-45.

[10] 徐运亭,徐启,郭永贵,等.低渗透油藏渗流机理研究及应用[M].北京:石油工业出版社,2006:64-66.

[11] 何贤科,陈程.低渗透油田建立有效驱替压力系统研究[J].特种油气藏,2006,13(2):56-57.

[12] 吴柏志.低渗透油藏高效开发理论与应用[M].北京:石油工业出版社,2009:80-83.