有限容量Geom/Geom/1/MWV离散时间排队

,,

(1.燕山大学 里仁学院 数学系,河北 秦皇岛 066004；2.燕山大学 理学院 应用数学系,河北 秦皇岛 066004)

0 引言

与计算机网络的发展相适应,离散时间排队系统的研究得到了广泛的重视,田乃硕等[1]的专著比较系统的介绍了离散时间排队系统．由于实际条件的限制,有限容量系统的研究具有现实意义,田乃硕[1]等和杜欣欣[2]等研究了Geo/Geo/1/N型离散时间单重工作休假排队,我们讨论的是有限容量Geom/Geom/1/N多重工作休假离散时间排队系统,系统容量为N,当系统中顾客数为N时,新到达顾客不进入系统,自动消失．图1为模型示意图．

1 拟生灭链模型的建立

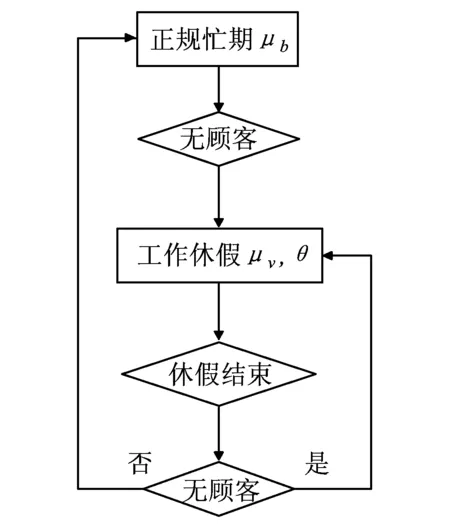
图1 模型示意图

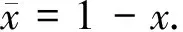
(a)系统容量为N,当系统中顾客数为N时,新到达的顾客消失．

(b)潜在的顾客到达发生在时隙末端(n-,n)处,到达间隔独立同分布:A～Geom(p)

(c)正规忙期,服务开始和结束均发生在时隙分点t=n,顾客服务时间相互独立同分布:Sb～Geom(μb)

(d)正规忙期某个服务结束后,若系统内无顾客,则进入工作休假,开始和结束均发生在时隙分点t=n,工作休假时长:V～Geom(θ)

工作休假期间,每个服务开始和结束亦发生在时隙分点t=n,服务时间相互独立同分布Sv～Geom(μv)

(e)当一个工作休假结束后,若系统中无顾客,进入下一个独立同分布的工作休假;若有顾客,服务率升至μb,进入正规忙期．

(f)顾客接受完服务立即离开系统,即顾客离开发生在时刻t=n,服务机制为先进先服务(FIFO)．

(g)到达间隔A,休假时长V,服务时间Sb,Sv,相互独立．

2 状态转移概率阵

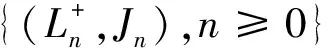
Ω={(k,j)|1≤k≤N,j=0,1}∪{(0,0)}.

对状态按字典顺序进行排列,可得其转移概率阵

(1)

其中

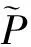
3 稳态下联合分布

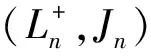
定理1 (L+,J)的联合概率分布为

(2)

其中

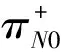
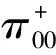
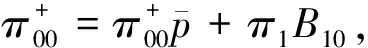
(3)

(4)

当2≤k≤N-1时,由πk=πk-1A0+πkA1+πk+1A2,可得

(5)

由πN=πN-1A0+πNB0,可得

(6)

由(6)第一式,可得

(7)

由(5)第一式,可得二阶逆向递推公式,即二阶齐次差分方程

(8)

解此差分方程可得通项．再由(4)第一式可得π00．

由式(3)可得π11,把(4)两式相加,整理得

(9)

可得π21,把(5)两式相加,整理得3≤k≤N时的递推公式

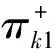
(10)

由式(9)、式(10)可得πk1,3≤k≤N.

4 稳态指标

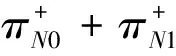
定理2 消失概率

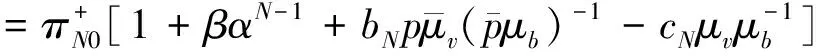
(11)

由稳态分布,易得

定理3 稳态下系统处于各状态的概率,即状态变量J的边缘分布

(12)

其中

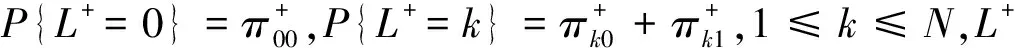
定理4 稳态下队长L+具有母函数(PGF)

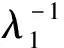
(13)

其中

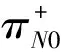
由式(13)易得稳态下系统中平均队长

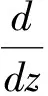
(14)

这里f′(z)=[(z-zN+1)(1-z)-1]′=[1-(N+1)zN+NzN+1](1-z)-2．

用H0表示工作休假期间系统中顾客数小于N且到达的顾客需要等待的概率,H1表示正规忙期系统中顾客数小于N且到达的顾客需要等待的概率,有

其中

应用文[1]中引理,并仿照其中的定理的证明过程,可得如下结果：

定理5 稳态下某顾客的等待时间W的PGF

(15)

其中

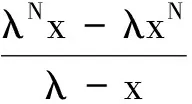
5 总结

通过对有限容量Geom/Geom/1多重工作休假离散时间排队系统的研究,我们得到了该模型的顾客消失概率、队长的PGF和平均队长、顾客等待时间的PGF等稳态指标．今后可继续对由本系统得到的结果进行随机分解、忙期分析,还可添加启动期、关闭期、N-策略等排队策略,使模型能更好的模拟现实复杂系统,为决策者们提供帮助．

[1]田乃硕,徐秀丽,马占友.离散时间排队论[M].北京:科学出版社,2008:206-211.

[2]杜欣欣,赵国会,田乃硕,等.Geo/Geo/1/N型离散时间单重工作休假排队[J].运筹与管理,2008,17(3):58-63.

[3]Hunter J.Mathematical Techniques of Applied Probability[M].New York： Academic Press,1983.