湖西矿深部大断面软岩巷道支护的DDA数值研究

王雁冰，郭东明，薛华俊，李树荣

(1.深部岩土力学与地下工程国家重点实验室，北京 100083； 2.中国矿业大学(北京)力学与建筑工程学院，北京 100083)

近年来，随着矿井开采深度的不断加大，巷道大变形、高地压、难支护的工程问题日益严重。深部岩体的结构、强度、变形、破断等力学特性变异复杂，导致巷道表面位移增加，返修量剧增，巷道维护变得异常困难，尤其是大断面软岩巷道这种问题更为突出。目前，对于深部采矿工程，主要采取锚杆、锚索等联合支护方式，对一些极破碎围岩采用锚注进行加固，均获得了一定效果。这些技术主要是通过支护，提高围岩岩体强度，改善围岩应力状态，以达到控制围岩松动圈的过度发展，保证围岩的稳定[1-5]。长期以来，人们试图从理论上分析和研究巷道的变形，并提出支护设计，但由于问题的复杂性，很难给出精确的解析解。数值模拟技术在解决此类问题中显示出巨大的优越性，取得了令人瞩目的成绩。不连续变形分析(Discontinuous Deformation Analysis)方法，兼有有限元法和离散元法的优点，较适合于模拟岩体结构的不连续大变形力学行为。本文通过不连续变形分析(DDA)方法，以湖西矿31102上顺槽深部大断面软岩巷道支护为研究背景，提出四种支护方案进行数值分析研究，从中择优并应用于现场，取得良好的效果。

1 概况

湖西矿位于山东省微山湖中部西岸。正常煤层厚度4.5m左右，结构简单，倾角5～15°，煤层以亮煤为主，镜煤、暗煤次之，玻璃光泽，裂隙较发育，性脆，易碎，f=1.5左右，煤岩类型为半亮型。由于受构造影响，开门后350m范围内，局部煤层厚度可能变薄，甚至缺失。煤层顶板为泥岩，其单轴抗压强度为18.4MPa；底板大成分为泥岩, 单轴抗压强度为15.8MPa。顶板与煤层都比较软，煤层顶底板岩性特征，如表1所示。31102工作面位于-750m水平，上顺槽巷道地面位于昭阳湖区，井下位于胶带大巷西北侧，服务于31102工作面的进风、行人、运输、管线敷设。巷道采用矩形断面，净宽4.5m，净高4.8m，属深井大断面软岩巷道。

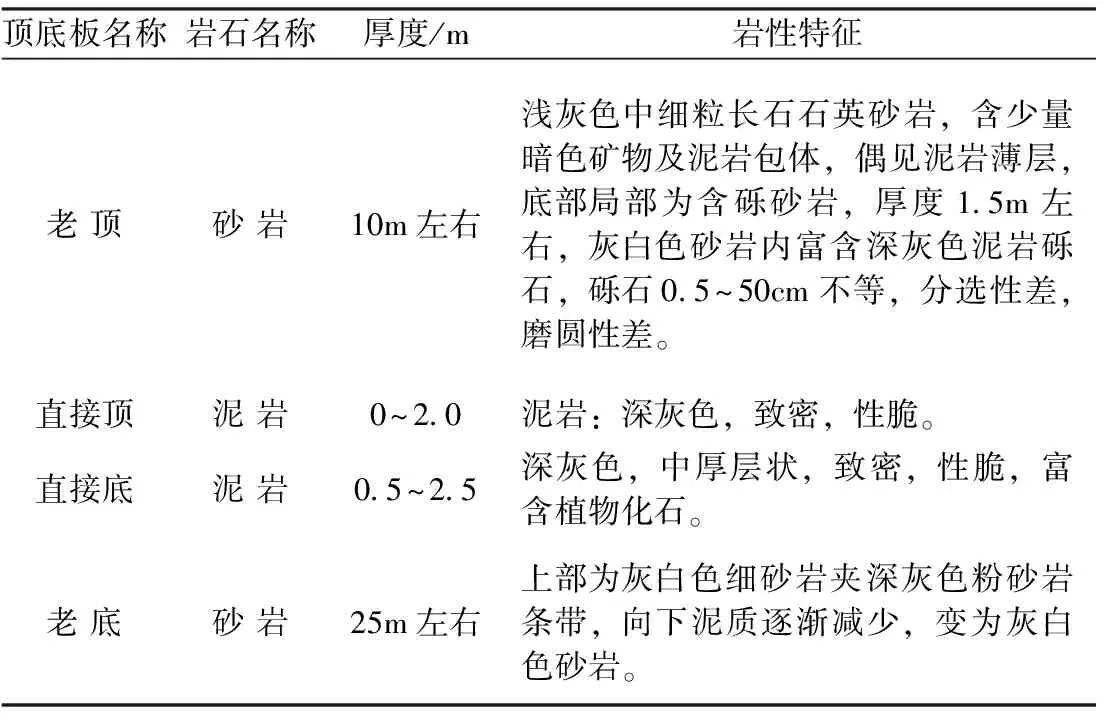
表1 煤层顶底板岩性特征

2 数值模拟研究

2.1 DDA基本理论

DDA法把结构面切割而成的块体单元作为基本单元，有描述块体运动的位移形函数，选择位移为联立方程式的未知数，利用最小势能原理建立控制方程[6]。当块体系统中每个块体的几何条件、边界条件及力学条件确定后，由DDA法就可以计算块体系统中每个块体的位移、应变及应力，从而确定块体间相对移动及滑动。因此，DDA方法可以模拟出块体的移动、转动、张开、闭合等全部过程，并据此判断块体系统的破坏情况。

2.2 模型的建立

选取31102上顺槽巷道中部具有代表性的局部区段进行模拟。根据该区段的地质资料，使用2D-DDA程序，将实际巷道情况简化为沿巷道横切面的二维平面应变块体模型，模型计算域为25m×20m，共划分为650个块体。模型底面和侧面采用固定约束。巷道距地表距离H=750m，取上覆岩层近似平均密度ρ= 2.60×103kg/m3，为了模拟地应力的作用，巷道所在位置的垂直地应力近似为：σ1=ρgH= 19.5 MPa。现场估测水平构造应力略大于垂直地应力，取构造应力σ2=20 MPa。根据已有的工程地质剖面图和岩体的结构特征，划分DDA模型的单元网格。计算域分为5个材料区域，如图1所示。在巷道周围布置了4个测点，记录测点的位移变化，测点①监测顶板位移；测点②监测底部位移；测点③监测左帮位移；测点④监测右帮位移。图2为初始模型。表2给出了岩层的力学参数。

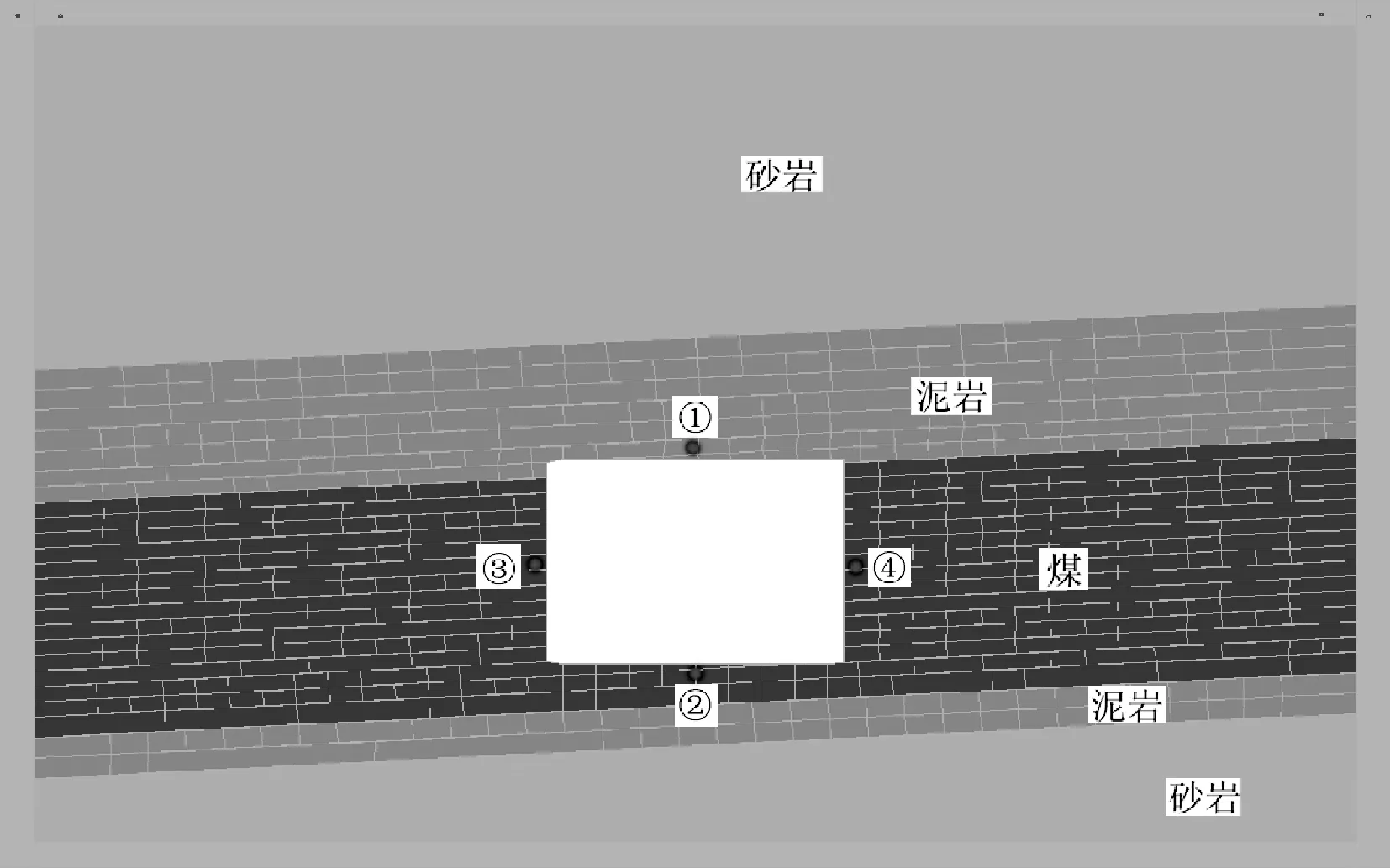
图1 模型层状材料区域及测点布置

图2 建立初始模型

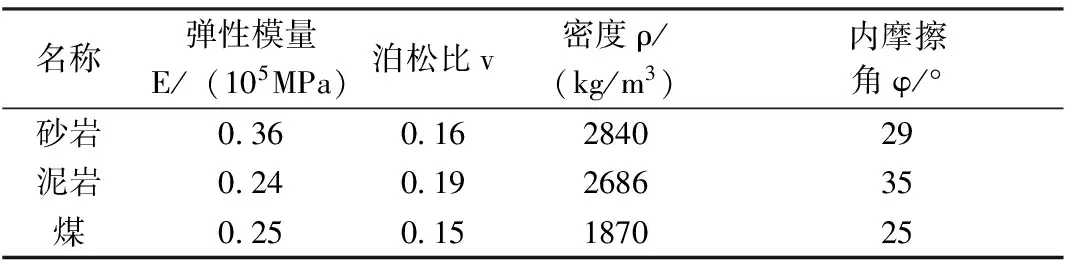
表2 典型岩层力学参数

2.3 无支护情况下DDA模拟巷道的变形破坏

运行2D-DDA程序时，经过反复试算，设计时间步为0.01，步位移取0.001，弹簧刚度取1000000，设置步数为3000步。

图3为无支护情况下DDA模拟巷道的变形破坏，在高地应力作用下，顶板破坏较严重，大量的块体散落到巷道底部，形成堆积，破坏范围大约为2m。底板破坏，底鼓较严重，由监测点②获得的数据知，底部位移约为0.4m。两帮无明显的破坏，但由监测点③、④知，左帮、右帮处块体的位移均约为0.3m，两帮在高地应力作用下移近量较大，局部块体变形严重，但没有出现块体的跨落。顶板应该加强支护，同时要防止较大底鼓的出现。

2.4 设计方案

根据上文无支护条件下巷道破坏的数值模拟情况，结合巷道的用途和服务年限、矿山压力和岩石的物理学性质、巷道的断面形状，与相似工程类比，初步设计了四种支护方案，见表3。其中，锚杆长度2.2m，锚索长度4.5m。

2.5 模拟结果及分析

图4和图5是方案2和方案4模拟后的效果图，从图上并未看出巷道有明显的破坏，方案4中顶板出现明显的离层，但没有块体散落。

表3 支护方案初步设计

图3 无支护情况下DDA模拟巷道的变形破坏

图4 方案2模拟效果

图5 方案4模拟效果

图6是4种方案中，顶、底、左帮、右帮位移监测曲线。由各条曲线知：变形速率先增大后减小，开始运算时，初始荷载施加到块体上，巷道空间成为应力释放区，块体迅速变形。变形到一定程度后，由于锚杆(索)的作用，巷道周围的块体变为整体，巷道表面块体的变形受到抑制，约2500步时，变形趋于稳定。四种方案的顶板最大位移量依次为：163.3mm、20.0 mm、24.6 mm、266.7 mm；底部的最大位移量依次为：37.2 mm、10.6 mm、6.8 mm、92.4 mm；左帮的最大位移量依次为：17.3 mm、9.8 mm、17.3 mm、20.5 mm；右帮的最大位移量依次为：15.9 mm、8.6 mm、14.8 mm、12.5 mm。方案1中，顶锚杆的数量少，间排距大，顶板变形量较大。方案2中，顶板、左帮、右帮位移量均为最小，底部位移仅为10.6 mm。方案3中，帮锚杆数量少，间排距大，但两帮的位移量较其他方案相比，并未明显增大，说明帮锚杆的数量和间排距对于控制两帮的位移未发挥很大作用。方案4中，仅用2根锚索，顶板破坏较严重，出现了明显的离层，由此说明其他三种方案中三根锚索的功用各不相同，中间锚索是控制顶板位移的，而两边的锚索是转移上覆岩层应力到深部去，充分发挥了锚索的支护作用。综合分析认为，方案2的支护效果最佳，将此方案应用于湖西矿31102上顺槽深部大断面软岩巷道支护中。

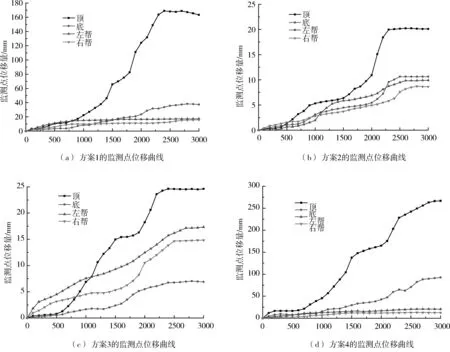
图6 4种方案中顶、底、左帮、右帮位移监测曲线图

3 支护效果检验

在湖西矿31102上顺槽，对方案2的设计进行了试验，同时对试验巷道进行了支护后的表面位移收敛、顶板离层量的现场监测，以检验设计效果。

3.1 现场支护及测站布置

巷道沿煤层顶板掘进，支护为锚网索配合钢带、钢筋梯子联合支护形式。顶部采用Φ20mm×2200 mm圆钢等强锚杆，帮部为Φ20mm×2200 mm全螺纹锚杆，顶板锚杆间排距为750mm×1000mm，两帮锚杆间排距为800mm×1000 mm；锚索间排距为1500mm×2000mm，长度为4.5～12 m，锚入稳定岩层中的长度不少于1.5 m，锚索呈三花型沿巷道分布；全断面挂菱形金属网，网与网压茬100 mm，每200 mm用10#铁丝联接一处。锚固采用树脂药卷锚固，锚杆及锚索锚固剂型号顶部为K2350型，帮部为K2850型。本次矿压观测安装表面位移观测点三处，顶板离层观测点三处。

3.2 表面位移监测

表面位移采用“十”字点测法。通过三个测站的实时监测，选取具有代表性的两测站数据进行分析，数据分析如图7所示。可以看出，巷道的顶底移近量30～35mm，两帮的收敛量在20mm左右，与数值模拟结果基本吻合。

3.3 顶板离层观测

通过对顶板离层测站的监测，选取两个测站数据进行分析，见图8和图9。由图8可见，巷道顶板最大离层量为7mm，其中锚固区内顶板离层量为31mm，锚固区外顶板离层量为38mm。图9所示的2号测站顶板总离层量3mm，其中锚固区内离层量为20mm，锚固区外离层量为23mm。两个测站的共同特点是，离层是在1～3d的短时间内持续完成。该离层量较小，说明方案2的支护效果良好。

3.4 监测结果分析

根据上述监测数据，巷道的顶底移近量为30～35mm，两帮的收敛量为20mm左右，两个测站测试顶板离层在3～7mm之间，顶板稳定，表明该巷道基本上未发生顶板离层，这表明方案2支护方式安全程度高。这也说明了采用DDA数值分析软件，在进行巷道锚杆(索)支护设计上，具有较好的可靠性。

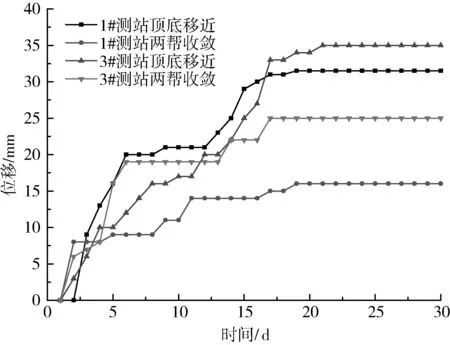
图7 巷道表面位移变化曲线

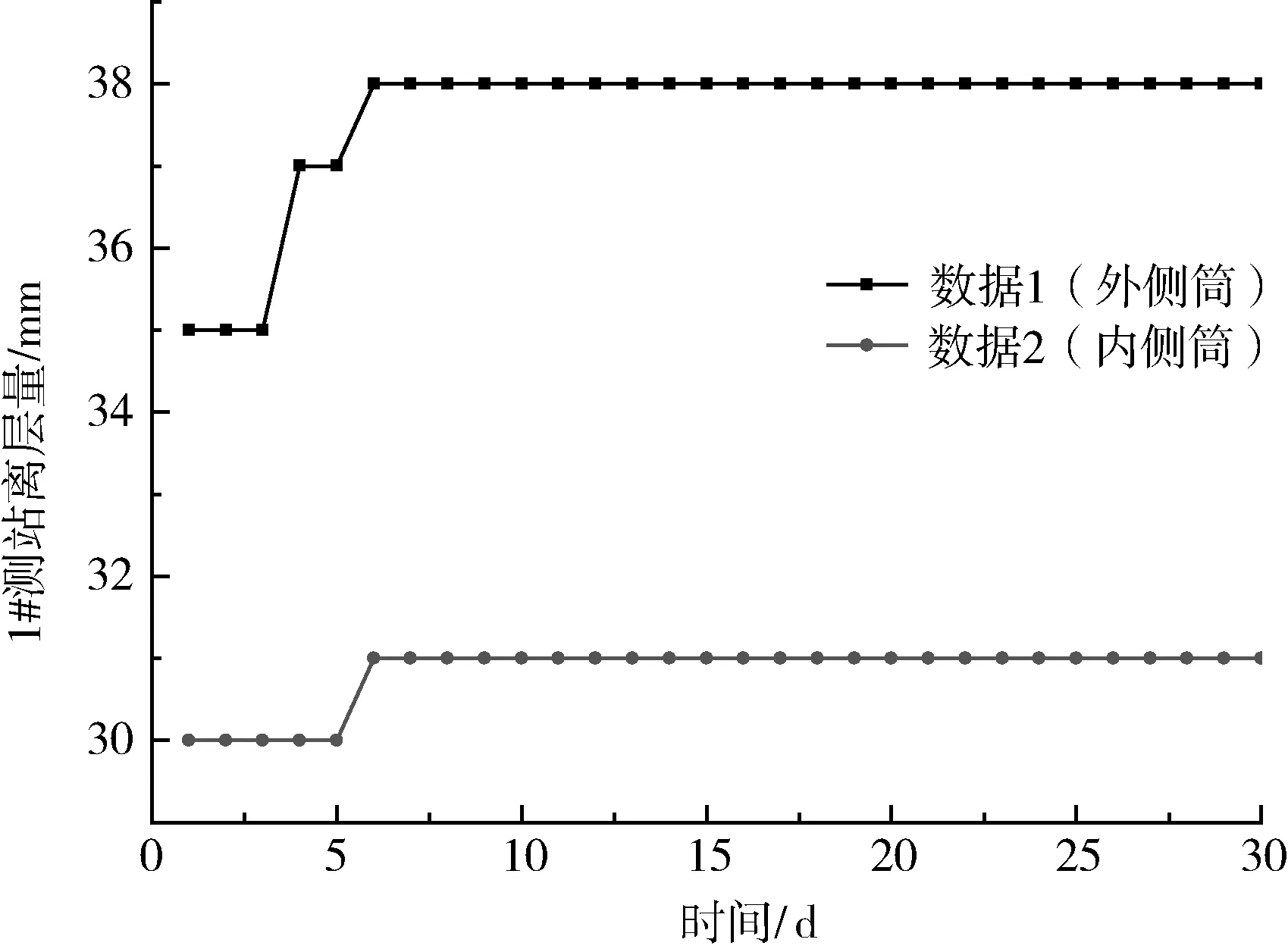
图8 1号测站顶板离层曲线

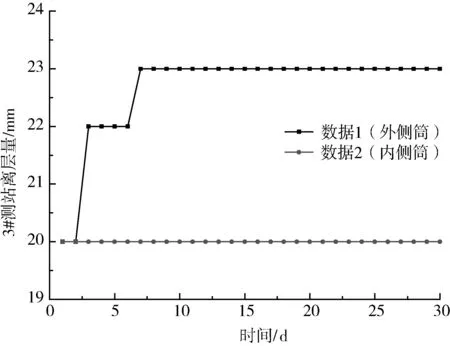
图9 3号测站顶板离层曲线

4 结论

1)数值分析及现场矿压观测结果表明：在湖西矿31102上顺槽深部大断面软岩巷道支护中，方案2(锚杆长度2200mm，顶锚杆间排距750mm×1000mm，帮锚杆间排距800m×1000m，锚索长度4500mm，间排距1500mm×2000mm)是最优的，该方案可保证煤层顶板的完整性，有利于巷道的支护效果。

2)采用不连续变形分析(DDA)方法，再现了巷道在不同支护形式的变形破坏过程，获得了锚杆(索)联合支护形式下，巷道在外部荷载作用下的变形量和破坏形式；同时，现场矿压监测数据与DDA计算结果较为吻合，说明了DDA数值分析方法可为巷道锚杆支护参数设计提供参考。

[1] 何满潮, 袁和生, 靖洪文，等. 中国煤矿锚杆支护理论与实践 [M]. 北京: 科学出版社, 2004.

[2] 董方庭. 巷道围岩松动圈支护理论及应用技术 [M]. 北京: 煤炭工业出版社, 2001.

[3] 柏建彪, 侯朝炯, 杜木民，等. 复合顶板极软煤层巷道锚杆支护技术研究 [J]. 岩石力学与工程学报, 2001, 20(1)：53-56.

[4] 张玉国, 谢康和, 何富连，等. 锚网索支护软煤综放面开切眼围岩稳定性研究 [J]. 岩石力学与工程学报, 2004, 23(19)：3 298-3 304.

[5] 康红普, 林健, 张冰川. 小孔径预应力锚索加固困难巷道的研究与实践 [J]. 岩石力学与工程学报, 2003, 22(3)：387-390.

[6] 石根华著，裴觉民译. 数值流形方法与非连续变形分析 [M]. 北京: 清华大学出版社, 1997.