风动潜孔锤反循环钻井最小注气量模型

黄 勇，殷 琨，朱丽红

(1.吉林大学建设工程学院，吉林长春 130026;2.吉林大学国土资源部复杂条件钻进技术开放研究实验室，吉林长春 130026;3.吉林大学国土资源部地球探测技术与仪器重点实验室，吉林长春 130026;4.中国石油大学 石油工程学院，山东 青岛 266555)

风动潜孔锤反循环钻井最小注气量模型

黄 勇1，2，3，殷 琨1，2，3，朱丽红4

(1.吉林大学建设工程学院，吉林长春 130026;2.吉林大学国土资源部复杂条件钻进技术开放研究实验室，吉林长春 130026;3.吉林大学国土资源部地球探测技术与仪器重点实验室，吉林长春 130026;4.中国石油大学 石油工程学院，山东 青岛 266555)

根据风动潜孔锤反循环钻进技术的特点，借鉴最小动能法推导出风动潜孔锤反循环钻井满足携屑能力的最小注气量和中心通道内最低井底压力，二者耦合得出风动潜孔锤反循环钻井最小注气量模型，结合GQ-320型潜孔锤工程算例，计算出不同机械钻速下最小注气量，并将模型计算结果与现场实测气量值进行比较。结果表明：在地层条件完整或漏失不严重的情况下，风动潜孔锤反循环钻井最小注气量计算值与现场实测值吻合较好;实例井上返岩屑的速度分析与现场未洗井情况一致，验证了模型的可靠性。

气体钻井;潜孔锤;反循环;注气量

风动潜孔锤反循环钻井技术是气体钻井技术的重要分支，集潜孔锤冲击碎岩、流体介质全孔反循环、连续上返岩矿心三项钻进工艺于一体，兼有空气钻井、冲击回转钻井和反循环钻井的优势。钻井过程中，循环的气体体积流量要保证井底清洁，岩屑及时顺畅排出和潜孔锤在孔底做功的需要。但是，空气的压缩性使实际体积流量随井深的增加而逐渐减小，造成孔底潜孔锤工作不正常、岩屑重复破碎、钻孔效率下降。为保证钻进顺利进行应随井深调节地面最小注气量，而关于反循环钻井地面最小注气量调节的可供经验并不多，还缺乏用于实际的理论方法和计算公式。若地面注气量过小，井内岩屑不能及时顺畅排出并逐渐聚集在井底，会导致重复破碎，同时潜孔锤在孔底不能正常工作，最后气量持续降低，井口压力持续升高，直到上返岩屑量越来越少，形成阻塞发生井下事故［1-3］。笔者借鉴最小动能法基本思想推导满足携屑能力的最小注气量计算公式，结合反循环钻头贯通孔结构和反循环钻井工艺的特殊性推导中心通道内最低井底压力计算公式，二者耦合得出风动潜孔锤反循环钻井最小注气量模型。

1 模型推导

风动潜孔锤反循环钻具的主要特征是双通道，即环状间隙和中心通道。受钻具结构和几何尺寸的限制，双通道过流断面固定且值很小。风动潜孔锤反循环钻进技术采用压缩空气作为钻井循环介质，流体介质上返速度高，岩屑颗粒之间、岩屑颗粒与压缩空气之间的相互作用较弱。风动潜孔锤反循环钻井技术当前主要用于钻直井，因此假设［4-10］：①直井钻进;②忽略岩屑颗粒和设备器壁的端末效应影响;③钻进中循环的气体满足理想气体状态方程;④气体和岩屑颗粒的混合物为具有相同密度和流速的均一流体;⑤中心通道和环状间隙内均处于紊流完全粗糙区。

风动潜孔锤反循环钻井中压缩气体流动过程如图1所示。

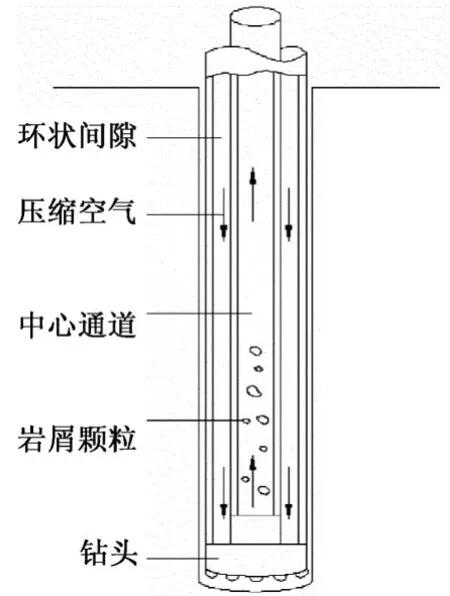
图1 反循环流动示意图Fig.1 Schematic diagram of reverse circulation flow

压缩空气沿双壁钻具的环状间隙进入孔底，驱动潜孔锤做功后携带反循环钻头钻进产生的岩屑沿中心通道上返至地表。结合反循环钻头钻取岩屑的不规则形状和反循环钻井工艺的特殊性，推导风动潜孔锤反循环钻井最小注气量模型。

1.1 最小携岩能力

为保持井底清洁，避免重复破碎，应将反循环钻头钻进产生的岩屑及时顺畅地排至地表。假设井眼内某一井深处的流体具有标准状态下空气的最小携岩能力，根据动能定理则有

式中，γgo为标准状态下气体的重度，N/m3;vgo为标准状态下所需最小气体流速，m/s;γg为计算井深处气体重度，N/m3;vg为计算井深处气体流速，m/s。

由理想气体状态方程可得任意计算井深处气体的重度为

式中，Sd为气体的相对密度;pgo为标准状态下气体压力，Pa;Tgo为标准状态下气体的绝对温度，K;p为计算井深处的压力，Pa;T为计算井深处的绝对温度，K。

任意计算井深处气体的体积流量Qg为

式中，Qgo为标准状态下的气体体积流量，m3/s。

由式(3)可推出计算井深处气体的流动速度vg为

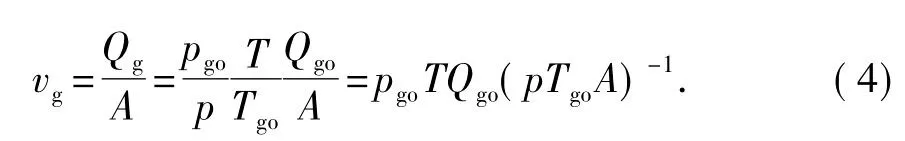
式中，A为计算井深处的过流断面面积，m2。

将式(2)和式(4)代入式(1)中整理得

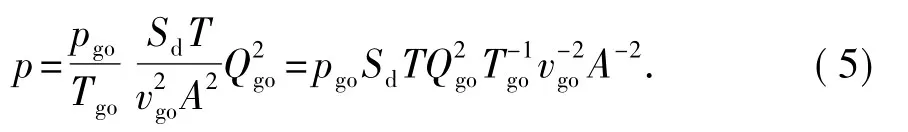
井内压缩空气若要具有标准状态下流速为vgo的气体携岩能力，则注气量与中心通道内井底压力须满足式(5)。

1.2 中心通道井底压力

由于反循环钻井工艺的特殊性，岩屑颗粒、压缩空气、地层流体构成中心通道内向上流动的三相流。在距地表一定井深处取一微元段dz，该微元段内压力梯度dp随井深z的变化而变化：一部分是由多相流运动产生的压力，一部分是由多相流自身重力产生的压力。根据圆形直管阻力损失范宁公式和伯努利方程，推导出微元段内多相流的压力变化dp与井深z的关系为

式中，γm为中心通道内混合均匀流重度，N/m3;Dc为中心通道直径，m;g为重力加速度;f为范宁摩擦系数;v为中心通道内气体上返流速，m/s。

中心通道内压缩空气、固体岩屑和液态地层流体混合物的重度γm为

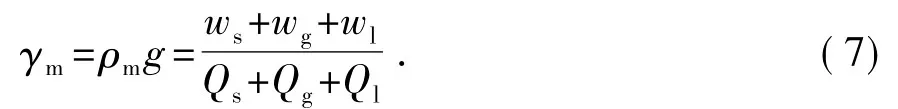
式中，wg、wl、ws分别为气体、液体、固体的重力流量，N/s;Qg、Ql、Qs分别为气体、液体、固体的体积流量，m3/s。

在风动潜孔锤反循环钻井循环系统中，中心通道内液流和岩屑的体积分数都很小，故只考虑气体体积流量的影响。然而，压缩空气的体积流量是井深的函数，根据质量守恒定律推出井内任意点压缩空气的重力流量、重度和体积流量之间的关系为

根据理想气体状体方程整理式(8)后得到任意一点压缩空气的体积流量为

忽略固体岩屑体积和液流体积的影响，将式(9)代入式(7)得到风动潜孔锤反循环钻井系统中心通道内任一点的重度为

式中，Sl为液相地层流体相对清水的相对密度;ρs、ρg和ρair分别为岩屑密度、气体密度和标准状态下空气密度，kg/m3;ρw为清水密度，kg/m3;Mair为空气摩尔质量，g/mol;Dbit为钻头外径，m;vm为机械钻速，m/s。

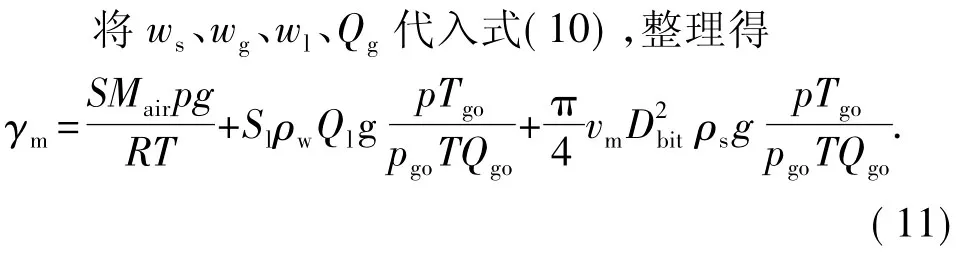
在计算井深处，中心通道内气体上返流速为

式中，Ac为中心通道过流断面面积，m2。

假定中心通道内压缩空气上返流速约为三相流体上返速度，将式(11)和式(12)代入式(6)中得

给定边界条件：在地表出口(z=0)处压力为ps，在井深z处压力为pcz，对式(13)进行积分得

令中心通道井底压力与最小携岩能力满足的压力相等，将式(14)代入式(5)整理得

式(15)即为风动潜孔锤反循环钻井最小注气量模型，求解该方程可得到不同井深条件下所需的最小注气量。

1.3 模型校正

式(15)计算的最小注气量是标准状态下所需的空气量，不能直接用于指导地面注气量的调节，须根据现场压力、温度和湿度进行校正。根据理想气体状态方程将现场压力和温度校正为

式中，pa为现场大气压，Pa;Ta为现场温度，K;Qa为校正后的注气量，m3/h。

考虑压缩机的除水效率，空气湿度校正［11］为

式中，Qh为湿气体的体积流量，m3/h;fw为除水效率;φ为相对湿度;pw为水蒸气的饱和压力，kPa。

2 算例分析

2.1 算例数据

结合GQ-320型油气勘探用风动潜孔锤反循环钻井系统及其在四川某井钻进的地层条件给出模型计算基础数据：中心通道出口压力ps为101.325 kPa，标准状态下压力 pgo为101.325 kPa，气体相对密度Sd为1，管壁粗糙度 Ra为3.81 μm，固相岩屑密度ρs为2700 kg/m3，井深z为2 km，除水效率fw为0.95，钻头直径Dbit为0.45 m，环状间隙外径Do为0.105 m，环状间隙内径Di为0.089 m，中心通道直径Dc为0.08 m，空气绝热指数k为1.4，空气摩尔质量Mair为0.029 kg/mol，相对湿度φ为0.8。

2.2 计算求解

风动潜孔锤反循环钻井最小注气量模型中各系数均是气量的函数，需要迭代求解。计算流程如图2所示。输入基本参数后给定计算初值，以允许误差er作为判断收敛标准，采用Newton迭代法进行计算，给定机械钻速即可得到不同井深条件下的最小注气量变化曲线。

图2 计算流程Fig.2 Calculation flow chart

不同机械钻速下计算得到的最小注气量随井深的变化曲线如图3所示。随着井深的增加，最小注气量增大，且机械钻速越大，相同井深处所需最小注气量越大。

2.3 结果对比

在四川某井应用风动潜孔锤反循环钻进技术，从开孔到600 m平均机械钻速为5 m/h，现场应用的实际气量如图4所示。井深0～550 m实际钻井所需气量与利用风动潜孔锤反循环钻井最小注气量模型计算的气量接近，到600 m时实际钻井所需气量剧增，这是因为550 m开始地层条件复杂，漏失严重。通过对比可知，在地层条件完整或漏失不严重的情况下，风动潜孔锤反循环钻井最小注气量模型

图3 最小注气量变化曲线Fig.3 Variation of the minimum gas volume flow rate

可以用来指导现场实际作业。

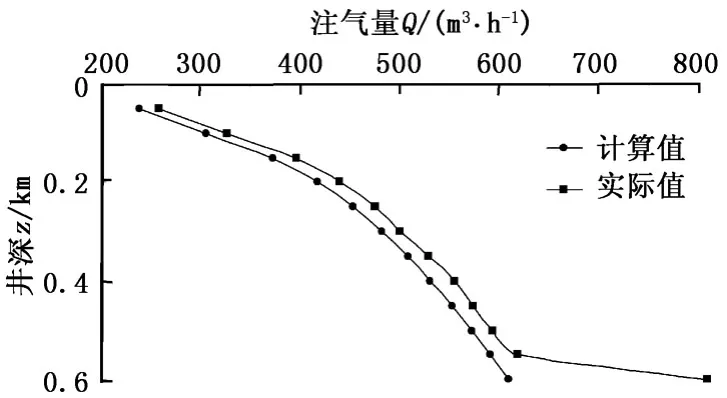
图4 实际注气量变化曲线Fig.4 Variation of actual gas volume flow rate

另外，比较Cray公式［12］计算实际钻进获取岩屑的最小上返速度与最小注气量模型计算岩屑的最小上返速度，进一步验证最小注气量模型。现场实际钻进获取的岩屑并非规整的球形颗粒，而是不规则形状。图5所示为风动潜孔锤反循环钻井上返的岩屑，不同编号的岩屑对应不同井深。将6块岩屑基于体积的当量球直径换算成当量球体，采用Cray公式计算携带岩屑至地表所需的最小气体上返速度。以1号岩屑为例，半径15.74 mm，最大高度22 mm，等效球体直径为34.87 mm，流道水力直径DH为76 mm，阻力系数CD为0.85，颗粒球形度ψ为1，最小上返速度为

图5 反循环钻头钻取的岩屑Fig.5 Cuttings drilled by reverse circulation drilling

同样采用Cray公式计算出其他5块岩屑的最小上返速度，再通过式(12)计算出机械钻速5 m/h条件下采用最小注气量模型时中心通道内压缩空气的上返流速，二者对比如图6所示。

通过上返流速对比可知，采用风动潜孔锤反循环钻井最小注气量模型计算的中心通道内气体上返流速大于采用Cray公式计算实际钻进获取岩屑的上返速度，不会产生岩屑堆积问题。这一结论与该井作业过程中未出现清洗情况相一致，进一步表明该模型可以用于分析和指导现场作业。

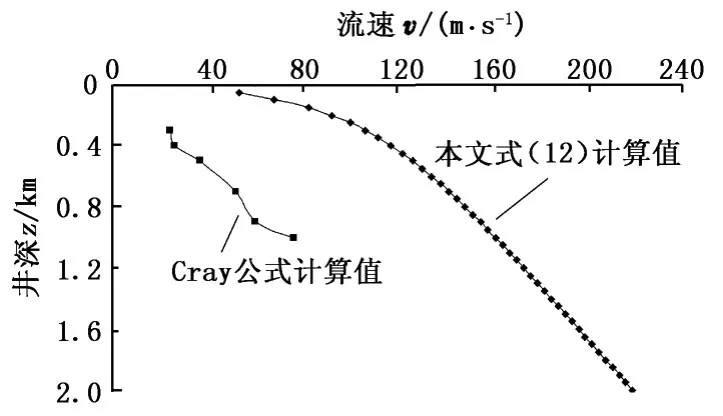
图6 上返流速对比曲线Fig.6 Comparison curve of up return flow rate

3 结论

(1)随着井深的增加，最小注气量逐渐增大，但并非简单的线性增加。

(2)在地层条件完整或漏失不严重的情况下，通过风动潜孔锤反循环钻井最小注气量模型计算得到的注气量与实例井的现场注气量接近，说明该模型可以指导现场作业。

(3)采用风动潜孔锤反循环钻井最小注气量模型计算的岩屑最小上返速度不会产生岩屑堆积问题，与现场未洗井情况一致，验证了模型的可靠性。

［1］张组培，殷琨，蒋荣庆，等.岩土钻掘工程新技术［M］.北京：地质出版社，2003.

［2］ 李世忠.钻探工艺学［M］.北京：地质出版社，1992.

［3］ 罗曼芦.气体动力学［M］.上海：上海交通大学出版社，1988.

［4］ANGEL R R.Volume requirements for air or gas drilling［R］.SPE 873-G，1957.

［5］IKOKU，AZAR J J，WILLIAMS C.Department of energy practical approach to volume requirements for air and gas drilling［R］.SPE 9445-MS，1980.

［6］宋洵成，管志川，陈绍维.斜井岩屑运移临界环空流速力学模型［J］.中国石油大学学报：自然科学版，2009，33(1)：53-56，63.

SONG Xun-cheng，GUAN Zhi-chuan，CHEN Shao-wei.Mechanics model of critical annular velocity for cuttings transportation in deviated well［J］.Journal of China University of Petroleum(Edition of Natural Science)，2009，33(1)：53-56，63.

［7］苏义脑，周川，窦修荣.空气钻井工作特性分析与工艺参数的选择研究［J］.石油勘探与开发，2005，32(2)：86-90，112.

SU Yi-nao，ZHOU Chuan，DOU Xiu-rong.Operation characteristics analysis and process parameters selection of air drilling［J］.Petroleum Exploration and Development，2005，32(2)：86-90，112.

［8］王存新，孟英峰，姜伟，等.气体钻井中井眼温度变化及其对注气量的影响［J］.天然气工业，2007，27(10)：67-69.

WANG Cun-xin，MENG Ying-feng，JIANG Wei，et al.Hole temperature variation and its effects on gas injection rate during gas drilling［J］.Natural Gas Industry，2007，27(10)：67-69.

［9］朱丽红，殷琨，刘建林，等.反循环气体钻井压力计算分析［J］.钻井液与完井液，2009，26(4)：34-37.

ZHU Li-hong，YIN Kun，LIU Jian-lin，et al.Pressure calculation and analysis of reverse circulation air drilling［J］.Drilling Fluid ＆ Completion Fluid，2009，26(4)：34-37.

［10］吴晓东，王庆，何岩峰.考虑相态变化的注CO2井井筒温度压力场耦合计算模型［J］.中国石油大学学报：自然科学版，2009，33(1)：73-77.

WU Xiao-dong，WANG Qing，HE Yan-feng.Temperature-pressure field coupling calculation model considering phase behavior change in CO2injection well borehole［J］.Journal of China University of Petroleum(Edition of Natural Science)，2009，33(1)：73-77.

［11］ 陆厚根.粉体技术导论［M］.上海：同济大学出版社，1988.

［12］郭柏云，格兰伯.欠平衡钻井气体体积流量的计算［M］.胥思平，译.北京：中国石化出版社，2006：9-18.

The minimum gas injection volume model of pneumatic DTH hammer reverse circulation drilling

HUANG Yong1，2，3，YIN Kun1，2，3，ZHU Li-hong4
(1.College of Construction Engineering，Jilin University，Changchun 130026，China;2.Laboratory of Technology for Drilling under Complex Condition of Ministry of Land and Resources，Jilin University，Changchun 130026，China;3.Key Laboratory of Geodetection Technology ＆ Instrumentation of Ministry of Land Resources，Jilin University，Changchun 130026，China;4.School of Petroleum Engineering in China University of Petroleum，Qingdao 266555，China)

According to the characteristics of pneumatic DTH hammer reverse circulation drilling technology，the minimum gas volume flow rate satisfying the minimum capacity of carrying scrap and the minimum bottom hole pressure within the central channel of pneumatic DTH hammer reverse circulation drilling were deduced using the kinetic energy method.Then，the model of the minimum gas volume flow rate of pneumatic DTH hammer reverse circulation drilling was established.Combined with the GQ-320 type DTH hammer practical work，the minimum gas volume flow rates under different penetration rates were obtained and compared with the measured values.The results show that under the condition of formation complete or the loss being not serious，the calculation values of the gas volume flow rate of the pneumatic DTH hammer reverse circulation drilling agree well with the field values.The upward cutting velocity analysis agrees well with the field data，which verifies the reliability of the model.

gas drilling;DTH hammer;reverse circulation;gas injection volume

TE 242.6

A

10.3969/j.issn.1673-5005.2011.05.012

1673-5005(2011)05-0065-05

2011－02－22

中国地质调查局项目(1212010816018);四川石油钻井工艺技术研究院项目(2006220100003435);山东省自然科学基金项目(ZR2011EEQ012)

黄勇(1981－)，男(汉族)，吉林永吉人，博士研究生，主要从事工艺冲击回转钻进技术研究。

(编辑 李志芬)