α-氨基酸癸胺衍生物缓蚀性能的理论评价

胡松青，郭爱玲，陈生辉，胡建春，张 军，郭文跃

(中国石油大学物理科学与技术学院，山东东营 257061)

α-氨基酸癸胺衍生物缓蚀性能的理论评价

胡松青，郭爱玲，陈生辉，胡建春，张 军，郭文跃

(中国石油大学物理科学与技术学院，山东东营 257061)

采用量子化学计算和分子动力学模拟相结合的方法，在液相条件下对2-氨基-N-癸烷-3-(4-羟基苯基)丙酸(A)、2-氨基-N-癸烷-乙酰胺(B)、2-氨基-N-癸烷-丙酸(C)和 2-氨基-N-癸烷-3-甲基-丁酰胺(D)4 种缓蚀剂分子抑制盐酸对低碳钢腐蚀的性能进行理论分析，考察其前线轨道能量、全局反应活性参数、Fukui指数、重原子对前线轨道的贡献，计算缓蚀剂分子与金属Fe(001)表面的吸附能。结果表明：缓蚀剂分子A具有最强的反应活性;缓蚀剂分子B拥有较高的局部反应活性，C次之，D最小;缓蚀剂分子与金属表面的结合力由强到弱依序为A、B、C、D;4种缓蚀剂分子的缓蚀性能由高到低依次为A、B、C、D，缓蚀性能与实验数据相吻合。

缓蚀剂;理论评价;量子化学计算;分子动力学模拟

α-氨基酸癸胺类缓蚀剂在抑制盐酸对低碳钢表面的腐蚀表现出良好的缓蚀性能。笔者采用量子化学方法和分子动力学方法［1-2］，以2-氨基-N-癸烷-3-(4-羟基苯基) 丙酸(A)、2-氨基-N-癸烷-乙酰胺(B)、2-氨基-N-癸烷-丙酸(C) 和 2-氨基-N-癸烷-3-甲基-丁酰胺(D)［3］4种缓蚀剂为研究对象，考察其在水溶液中的反应活性、结构特征及与金属表面的吸附行为，探索其缓蚀机制和溶剂水对吸附过程的影响，并对其缓蚀性能进行理论评价。

1 计算方法

1.1 量子化学计算

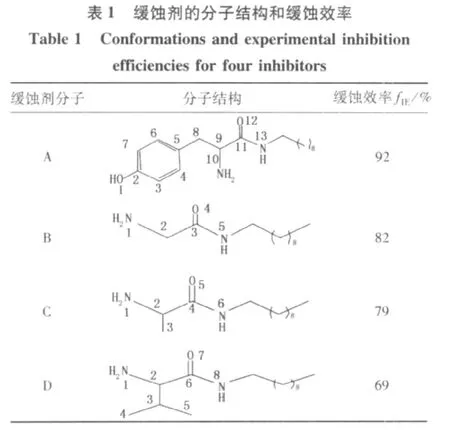
4种缓蚀剂的分子结构和缓蚀效率［4］见表1。缓蚀剂分子的初始构型均由Material Studio4.2程序包中的Visualizer模块构建。采用密度泛函中的广义梯度近似(GGA)［5］方法，在 DNP［6］基组下运用PW91［7］交换关联函数对所有分子进行几何全优化，并进行频率分析，保证所得结构为势能面上的极小点(无虚频)，而不会是过渡态或高阶鞍点，收敛精度为Fine。为进一步接近真实条件，在量化计算部分考虑了溶剂水［8］(介电常数为78.54 F/m)对缓蚀剂反应活性的影响。所有的计算均采用Dmol3模块完成。前线轨道能量、能隙、电荷分布、Fukui指数等量化参数均在同一基组水平上计算得出。

1.2 分子动力学模拟

采用三层结构模型研究液相条件下单分子缓蚀剂与金属表面的相互作用：①建立基底层的 Fe(001)［9］表面。表面厚度为11层，共计1 469个铁原子，3.153 nm×3.153 nm×7.782 nm;②采用AmorphousCell模块建立包含1个缓蚀剂分子和1000个水分子的中间层体系;③利用Amorphous Cell模块建立包含500个水分子的溶剂层结构。模拟中冻结基底层和第三层的水分子，采用Materials Studio 4.2软件包中的 COMPASS［10］力场对体系进行优化，正则系综(NVT)［11］的分子动力学模拟通过Discover模块完成。模拟温度为298 K，采用Anderson［12］方法进行温度控制。分子起始速度由Maxwell-Boltzmann分布随机产生，在周期性边界条件和时间平均等效于系综平均等假设基础上，运用Velocity Verlet［13］算法求解牛顿运动方程。分子间范德瓦尔斯和库仑相互作用通过Charge Group［14］方法计算，该方法所使用的基团势函数为

式中，Q、μ、θ和Θ分别为该基团所带总电量、偶极矩、电四极矩和方位角;R为基团中心所在的径向距离。截断半径为1.5 nm，截断距离之外的分子间相互作用能按平均密度近似方法进行校正。时间步长为1 fs，模拟时间为1000 ps，每1000步记录一次体系的轨迹信息。所有计算均在PentiumⅣ微机上进行。

2 结果分析

2.1 前线轨道分布

分子轨道是由原子轨道线性组合而成的单粒子波函数。根据前线轨道理论［15］，两种分子间的相互作用主要来自最高占有轨道(HOMO)与最低空轨道(LUMO)之间的作用。最高占有轨道能量(EHOMO)是分子供电子能力的量度，即EHOMO越大，分子越容易向低能级分子轨道提供电子;最低空轨道能量(ELUMO)是接受电子能力的量度，即ELUMO越小，分子越容易接受电子［16］。有机缓蚀剂分子 HOMO与LUMO之间的能隙(ΔE=ELUMO－EHOMO)也是评价缓蚀剂分子稳定性的重要因素。ΔE越小，缓蚀剂分子越稳定，其缓蚀性能越好［17］。水溶液中4种缓蚀剂分子的前线轨道分布如图1所示。

图1 水溶液中各分子的最高占有轨道(HOMO)、最低空轨道(LUMO)的0.02 au等值面图形Fig.1 HOMO and LUMO isosurfaces with a value of 0.02 au for molecules in solution phase

从图1可以看出，4个分子最高占有轨道与最低空轨道主要离域于其极性头部，当吸附作用发生时，极性头部优先吸附于金属表面，既有利于金属表面的空d轨道接受缓蚀剂分子所提供的电子形成配位键，也有利于缓蚀剂分子利用其反键轨道接受来自金属表面的电子而形成反馈键，使缓蚀剂分子在金属表面形成稳定吸附。这是由于羰基上的碳原子以sp2杂化轨道形成3个σ键，并且分布在同一个平面上，其中一个sp2杂化轨道和氧形成一个σ键，另外两个sp2杂化轨道和其他两个原子形成σ键。羰基碳原子上还剩下的一个p轨道和氧原子上的一个p轨道垂直于3个σ键形成的平面，侧面重叠形成π键。由于氧原子的电负性较大，有较强的吸电子能力，π电子云偏向氧原子，导致氧原子的电子云密度增加，使其与金属表面形成配位键。此外，两个氮原子都含有一对孤对电子，易与铁的空d轨道形成配位键，形成更加稳定的吸附。在分子A中，除了氮、氧原子外，由于酚羟基的氧原子处于sp2杂化状态，氧上有两对孤对电子，其中一对占据sp2杂化轨道，另一对占据p轨道，p电子云可以与苯环的大π键电子云发生侧面重叠，形成p－π共轭体系，使苯环上的电子云密度增加，有利于其与金属表面发生相互作用。缓蚀剂分子A无论从最高占有轨道能量、最低空轨道能量，还是能隙ΔE都具有明显的缓蚀优势。

2.2 全局反应活性

缓蚀剂分子的全局参数可通过密度泛函理论计算得出。化学势表示在一定的外加电场作用下体系总能量随电子转移的改变，其值可用来衡量电子反应活性的强弱［18］。单位电子转移后，能量改变越大，体系活性越高，越容易与金属基体发生反应。对于包含N个电子的体系，在外场v(r)一定的情况下，化学势(μ)等于电负性(χ)的负值，定义为体系总能量(E)对电子数(N)的一阶导数［19］，即

绝对硬度是表征缓蚀剂分子的稳定性与化学反应活性的重要参数。在密度泛函理论方法中，绝对硬度(η)定义为体系总能量E对电子数N的二阶导数［20］，即

全局软度［21］定义为

Parr等［22］引入亲电指数ω，用来衡量一个分子的亲电子能力大小，定义为

在分子轨道理论中，绝对硬度可用下式［23］近似计算：

在吸附过程中，单独考虑缓蚀剂分子的电子结构性能不足以真实地描述化学反应过程，因此必须同时考虑缓蚀剂分子和金属的电子性能。电子转移参数描述的是缓蚀剂分子与金属表面间的电子转移能力，其计算公式［18，24］如下：

其中，μI和μM分别为缓蚀剂分子和金属原子的化学势。

水溶液中4种缓蚀剂分子的全局活性参数见表2。

表2 水溶液中4种缓蚀剂分子的全局活性参数Table 2 Global reactivity parameters for four inhibitor molecules in solution phase

由表2看出：缓蚀剂分子A的化学势最小，单位电子转移后，分子A的能量改变较其他分子大，体系活性较高，易与金属基体发生反应;分子A具有较大的全局软度、亲电指数、电子转移数和较小的绝对硬度。这充分证明分子A与金属铁之间具有较强的相互作用，易吸附于金属表面，从而抑制其他腐蚀性离子的入侵，因此其缓蚀性能最好，且与实验数据相符［4］。缓蚀剂分子B、C、D的全局参数差别很小，不能作为衡量缓蚀性能的量度。

2.3 局部反应活性

化学势、绝对硬度、软度和亲电指数是从电子的固有属性进行推理的，其中包括原子电荷的计算、电子的自旋布局、电荷密度的拉普拉斯函数等方法。能够表征分子局部反应活性的最成功的方法是Fukui前线轨道理论［25］。

Fukui指数不但可以测定分子的化学反应点位的强弱，而且还可以确定活性区域的亲核或亲电子特性。为了进一步评价其他3种缓蚀剂分子的缓蚀性能，采用各重原子的Fukui指数进行分析。在外加势场v(r)一定的情况下，Fukui函数f(r)定义为电子密度ρ(r)对电子数N的一阶偏导［26-27］，即

根据有限差分近似，Fukui函数［2，4，29］f(r)可表示为

式中，qi(N)、qi(N+1)和qi(N－1)分别是分子为中性、阴离子和阳离子时，分子中原子i所带的电量;fi(r)+和fi(r)－分别为亲核攻击指数和亲电攻击指数，表示分子中原子i得或给电子能力的强弱，数值越大，得或给电子能力越强。

此外，对于某一特定分子，构成其HOMO-LUMO的每一原子轨道的HOMO-LUMO系数的平方，均正比于该原子轨道对分子HOMO-LUMO的贡献［28-30］。因此，可采用重原子对HOMO-LUMO的贡献衡量原子供或得电子的能力。计算公式［29］表示为

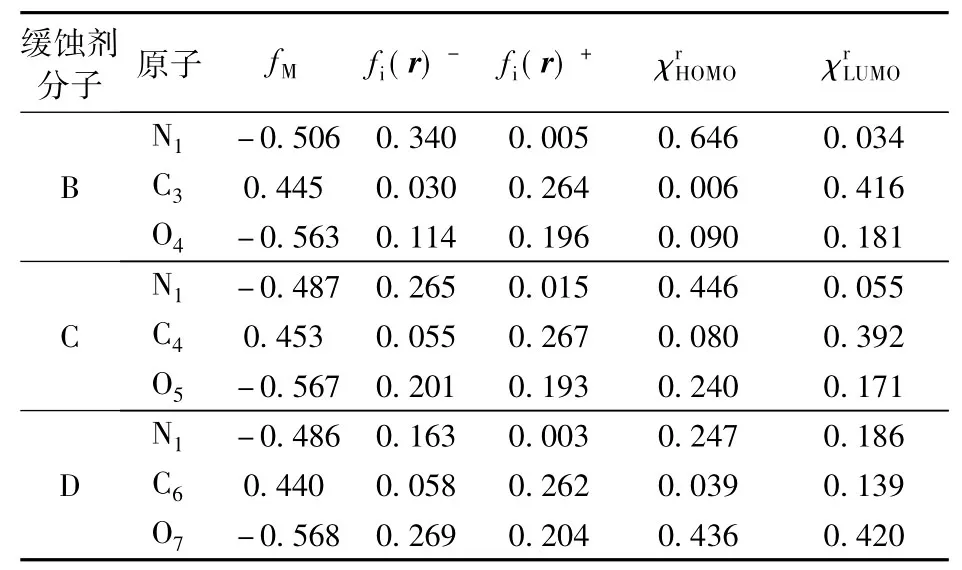
表3 分子B、C、D的Mulliken电荷分布、Fukui指数和重原子对HOMO、LUMO的贡献Table 3 Mulliken charge、Fukui index and contributions of heavy atoms to HOMO and LUMO for B，C and D

从表3中可以看到：碳原子带正电，表明具有亲电性，可能得到电子与金属表面形成反馈键;氮、氧均带负电表明具有亲核性，可能供出电子与金属表面形成配位键;3种分子的反应活性中心均集中在氮、碳和氧上;分子B中N1的fi(r)－最大，且对最高占有轨道的贡献最大，N1为分子B的亲核反应中心，具有最高的供电子能力;3种分子的给电子能力由强到弱顺序为B、C≈D;3种分子中碳的亲核攻击性最强，且其fi(r)+相差不多，但在最低空轨道的贡献中分子D最小，C、B较D具有更好的得电子能力，而C与B在碳原子上的得电子能力相差不多，对最高占有轨道的贡献也相差很小，因此碳点位的化学反应活性由强到弱顺序为B≈C、D;3种缓蚀剂分子的局部反应活性由强到弱依次为B、C、D。

2.4 缓蚀剂分子在Fe(001)表面的吸附行为

2.4.1 平衡吸附构型

体系平衡由温度和能量平衡加以判别。液相条件下4种缓蚀剂在Fe(001)表面的分子动力学模拟经300 ps均已达平衡，图2为液相条件下4种缓蚀剂分子在Fe(001)表面的平衡吸附构型。图中4种缓蚀剂分子的极性头部均吸附于Fe(001)表面，而由10个碳原子组成的烷基链由于溶剂水的作用发生扭转并偏离金属表面指向溶液。当体系达平衡后，缓蚀剂分子在其平衡位置附近做微小的振动，所不同的是烷基链偏离金属表面的程度和极性头部的驱替能力不同。

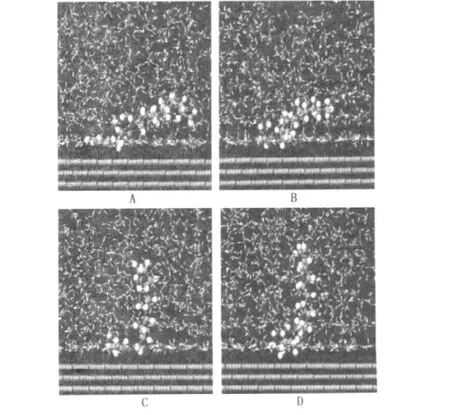
图2 液相中4种缓蚀剂分子在Fe(001)表面的平衡吸附构型Fig.2 Equilibrium configurations of inhibitors adsorbed on Fe(001)surface in liquid phase

为了细致描述缓蚀剂分子的平衡吸附形态，对—NH2中的氮原子、—C O中的碳原子和氧原子与金属铁表面的距离(d)分别测量，其统计平均值列于表4。从表4中可以看出，体系达平衡后，氮、碳和氧与铁表面的距离分别分布在0.294～0.504、0.279～0.378和0.244～0.270 nm，说明缓蚀剂分子在此3个位点具有较强的反应活性，与金属Fe(001)表面形成多中心吸附，且氧原子与表面的距离最近，碳原子次之，氮原子最大。

表4 缓蚀分子在液相中平衡吸附构型的结构参数Table 4 Structural parameters of four simulated molecules in liquid phase

从表4还可以看出，缓蚀剂分子的烷基链倾斜角由74°逐渐减小到31.14°，说明缓蚀剂分子在溶剂的作用下向金属表面“倒卧”能力减弱。这种现象与缓蚀剂分子头部极性和吸附形态有密切关系。缓蚀剂分子A的极性头部平行吸附于金属表面，增强了驱替水分子的能力，与金属表面结合更牢固;对于分子B、C、D，在其极性头部不同程度地加入了非极性基团，而且非极性基团所占的比重越大，越容易受到水分子的影响，因此削弱了缓蚀剂分子与金属表面的结合强度，导致其烷基链倾斜角逐渐减小。

2.4.2 能量分析

缓蚀剂分子的结构及能量参数均在体系达到平衡后提取。图3为缓蚀剂分子A动力学模拟过程的能量和温度随时间变化的波动曲线(B、C和D都具有相似的能量和温度分布曲线)。体系模拟过程中后300 ps的能量涨落约为0.30%，温度涨落为(298±10)K，表明体系已达平衡，由此选取后300 ps进行取样，计算相应缓蚀剂分子结构及能量参数的统计平均值。

图3 缓蚀剂分子A在Fe(001)表面吸附的能量和温度波动曲线Fig.3 Energy and temperature fluctuation curves of A on Fe(001)surface

液相条件下缓蚀剂分子在金属Fe(001)表面的平衡吸附形态有明显的差异，缓蚀剂分子与金属表面的吸附能及缓蚀剂分子的形变能见表5。由于缓蚀剂分子与金属表面之间吸附能在一定程度上能够反映缓蚀性能，其绝对值越大，缓蚀剂与金属表面的结合就越牢固，而形变能反映缓蚀剂分子在溶液条件下的变形程度，分别利用如下公式［31-32］进行计算：

其中，Ea为缓蚀剂与金属表面的吸附能;Em为孤立缓蚀剂分子的能量;Es为未吸附缓蚀剂时金属表面的能量;Em－s为缓蚀剂分子和金属表面体系的总能量;Ed为缓蚀剂分子在液相条件下的形变能;Eimb和Eim分别为缓蚀剂分子在束缚状态和自由状态下的单点能。

根据热力学原理，引起溶液中某种粒子在界面层中吸附的基本原因是由于吸附过程伴随着体系自由能的降低，即体系为放热过程，吸附能必须是负值［33］。其绝对值越大，说明缓蚀剂分子与金属表面的结合能力越强，其缓蚀性能越高。由表5看出，4种缓蚀剂分子的缓蚀性能由强到弱依次为A、B、C、D。4种缓蚀剂分子都发生了不同程度的形变，且随着非极性基团的加入，形变能逐渐增大，但其形变能均小于吸附能的绝对值，表明缓蚀剂分子能克服自身形变而吸附于金属表面。这与量子化学计算分析的结论相一致。

表5 缓蚀剂分子液相条件下吸附能和形变能的统计平均值Table 5 Statistic average values of adsorption energies and deformed energies for four inhibitors in liquid phase

3 结论

(1)4种缓蚀剂分子的最高占有轨道与最低空轨道主要离域于其极性头部，可与金属表面形成配位键和反馈键，其中分子A具有最大的最高占有轨道能量和最小的最低空轨道能量，且反应活性最强。分子B、C、D的反应活性中心均位于—NH2中的氮原子、—C O中的碳原子和氧原子上，与金属表面形成多中心吸附，缓蚀剂分子B的局部反应活性较C强，D最小。

(2)在Fe(001)表面发生吸附时，分子的极性头基优先吸附于金属表面，烷基尾链在水溶液的影响下以不同的倾斜角指向液体。由于头基的极性强弱和吸附形态的差异导致其与金属表面结合力由强到弱依次为A、B、C、D。4种缓蚀剂分子的缓蚀效率由高到低顺序为A、B、C、D，与实验结果一致。

［1］VOSTA J，ELIASEK J.Study on corrosion inhibition from aspect of quantum chemistry［J］.Corros Sci，1971，11(4)：223-229.

［2］ 林梦海.量子化学简明教程［M］.北京：化学工业出版社，2005：262-263.

［3］GOMEZ B，LIKHANOVA N V，DOMINGUEZ-AGUILAR M A，et al.Theoretical study of a new group of corrosion inhibitors［J］.Phys Chem A，2005，109：8950-8957.

［4］OLIVARES O，LIKHANOVA N V，GOMEZ B，et al.Electrochemical and XPS studies of decylamides of a-amino acids adsorption on carbon steel in acidic environment［J］.Applied Surface Science，2006，252：2894-2909.

［5］ DULAK M，KAMINSKI J W，WESOLOWSKI T A.E-quilibrium geometries of noncovalently bound intermolecular complexes derived from subsystem formulation of density functional theory［J］.Chem Theory Comput，2007，3：735-745.

［6］FRANZEN S.Carbonmonoxy rebinding kinetics in H93G myoglobin：separation of proximal and distal side effects［J］.Phys Chem B，2002，106：4533-4542.

［7］张军，赵卫民，郭文跃，等.苯并咪唑类缓蚀剂缓蚀性能的理论评价［J］.物理化学学报，2008，24(7)：1239-1244.

ZHANG Jun，ZHAO Wei-min，GUO Wen-yue，et al.Theoretical evaluation of corrosion inhibition performance of benzimidazole corrosion inhibitors［J］.Acta Phys Chim Sin，2008，24(7)：1239-1244.

［8］KHALEDA K F，FADL-ALLAHB S A，HAMMOUTIC B.Some benzotriazole derivatives as corrosion inhibitors for copper in acidic medium：experimental and quantum chemical molecular dynamics approach［J］.Materials Chemistry and Physics，2009，117：148-155.

［9］RAMACHANDRAN S，TSAI B L，BLANCO M，et al.Self-assembled monolayer mechanism for corrosion inhibition of iron by imidazolines［J］.Langmuir，1996，12(26)：6419-6428.

［10］SUN H.Compass：an ab initio force-field optimized for condensed-phase applicationss overview with details on alkane and benzene compounds［J］.Phys Chem B，1998，102(38)：7338.

［11］ HEERMANN D W.论物理学中的计算机模拟方法［M］.秦克成，译.北京：北京大学出版社，1996：45-47.

［12］BERENDSEN H J C，POSTMA J P M，VAN GURSTEREN W F.Molecular dynamics with coupling to an external bath［J］.Chem Phys，1984，81：3684-3690.

［13］ANDERSEN H C.Molecular dynamics simulations at constant pressure and/or temperature［J］.Chem Phys，1980，72：2384.

［14］ MAITLAND G C，RIGBY M，SMITH E B，et al.Intermolecular forces：their origin and determination［M］.London：Oxford University Press，1987：327-330.

［15］ BEREKET G，HUR E，OGRETIR C.Quantum chemical studies on some imidazole derivatives as corrosion inhibitor for iron in acidic medium［J］.Mol Struct(Theochem)，2002，578：79-88.

［16］KHALIL N.Quantum chemical approach of corrosion inhibition［J］.Electrochimica Acta，2003，48：2635-2640.

［17］TANER A，KANDEMIRLI F，EBENSO E E，et al.Quantum chemical studies on the corrosion inhibition of some sulphonamides on mild steel in acidic medium［J］.Corrosion Science，2009，51：35-47.

［18］LASHKARI M，ARHADI M R.DFT studies of pyridine corrosion inhibitors in electrical double layer：solvent，substrate，and electric field effects［J］.Chem Phys，2004，299：131-137.

［19］ PARR R G，DONNELLY R A，LEVY M，et al.Electrpnegativity：the density functional viewpoint［J］.Chem Phys，1978，68：3801.

［20］PARR R G，PEARSON R G.Absolute hardness：companion parameter to absolute electronegativity［J］.Am Chem Soc，1983，105：7512.

［21］YANG W，PARR R G.Hardness，softness，and the fukui function in the electronic theory of metals and catalysis［J］.Proc Nati Acad Sci USA，1985，82：6723-6726.

［22］PARR R G，SZENTPALY L，LIU S.Electrophilicity index［J］.Am Chem Soc，1999，121：1922.

［23］PEARSON R G.Absolute electronegativity and hardness correlated with molecular orbital theory［J］.Proc Nat Acad Sci USA，1986，83：8440-8441.

［24］ LASHGARI M，ARSHADI M R，PARSAFAR G A.et al.Cluster/polarized continuum models for density functional theory investigations of benzimidazole corrosion inhibitors at metal/solution interface［J］.Corrosion，2006，62：204.

［25］GOMEZ B，LIKHANOVA N V，DOMINGUEZ-AGUILAR M A，et al.Quantum chemical study of the inhibitive properties of 2-pyridyl-azoles［J］.Phys Chem B，2006，110(18)：8928-8934.

［26］LI T L，LIU S B，FENG S X，et al.Face-integrated fukui function：understanding wettability anisotropy of molecular crystals from density functional theory［J］.Am Chem Soc，2005，127：1364-1365.

［27］ BULAT F A，CHAMORRO E，FUENTEALBA P，et al.Condensation of frontier molecular orbital Fukui functions［J］.Phys Chem A，2004，108：342-349.

［28］COSTA J M，LLUCH J M.The use of quantum mechanics calculations for the study of corrosion inhibitors［J］.Corrosion Science，1984，24：929-933.

［29］张曙光.有机阻垢缓蚀剂作用机理的理论研究［D］.南京：南京理工大学化学系，2006.

ZHANG Shu-guang.Theoretical study on the operation mechanism of scale and corrosion inhibitors［D］.Nanjing：Department of Chemistry，Nanjing University of Science and Technology，2006.

［30］FANG J，LI J.Quantum chemistry study on the relationship between molecular structure and corrosion inhibition efficiency of amides［J］.Mol Struct(Theochem)，2002，593：179-185.

［31］KORNHERR A，TORTSCHANOFF A，ERWIN P C.Modelling of aqueous solvation of eosin Y at the rutile TiO2(110)/water interface［J］.Chem Phys Lett，2006，430：375-379.

［32］张曙光，王风云，雷武.水溶性聚合物与硬石膏晶体相互作用的分子动力学模拟［J］.化学学报，2007，65(20)：2249-2256.

ZHANG Shu-guang，WANG Feng-yun，LEI Wu.Molecular dynamics simulaton of interaction between water-soluble polymers and anhydrite crystal［J］.Acta Chim Sin，2007，65(20)：2249-2256.

［33］ 范洪波.新型缓蚀剂的合成与应用［M］.北京：化学工业出版社，2004：9-14.

Theoretical evaluation of corrosion inhibition performance of decylamides of α-amino acids derivatives

HU Song-qing，GUO Ai-ling，CHEN Sheng-hui，HU Jian-chun，ZHANG Jun，GUO Wen-yue
(College of Physics Science and Technology in China University of Petroleum，Dongying 257061，China)

The corrosion inhibition performances of four corrosion inhibitors in HCl on mild steel，including 2-amino-N-decyl-3-(4-hydroxyphenyl)propionamid(A)，2-amino-N-decylacetamide(B)，2-amino-N-decylpropionamide(C)and 2-amino-N-decyl-3-methylbutyramide(D)，were theoretically evaluated using quantum chemistry calculations and molecular dynamics simulations.Frontier orbital theory and global activity，Fukui indices and the contributions of heavy atoms to frontier orbital were studied.Adsorption energy of corrosion inhibitors on Fe(001)surface was calculated.The results indicate that inhibitor A shows the highest reaction activity among the four molecules.The inhibitor B displays higher local reaction activity，followed by C and D minimum.The order of bonding energy between corrosion inhibitors and metal surface is defined as A＞B＞C＞D.Quantum chemistry calculation and molecular dynamics simulations show that the order of corrosion inhibition property for four inhibitors is as follows A＞B＞C＞D，which agrees well with the experimental data.

corrosion inhibitor;theoretical evaluation;quantum chemistry calculation;molecular dynamics simulation

O 647;TG 174.42

A

10.3969/j.issn.1673-5005.2011.03.030

1673-5005(2011)03-0148-06

2011－01－25

中石化普光气田缓蚀剂技术研究专项课题(309003);中国石油中青年创新基金项目(2008D－5006－02)

胡松青(1967－)，男(汉族)，湖北松滋人，副教授，博士，研究方向为金属防腐。

(编辑 刘为清)