含连续整数的3维本原勾股数问题

袁 淑 丽

(东莞市经济贸易学校，广东 东莞 523106)

1 引言

在不定方程x2+y2=z2中有一类特殊的正整数解，3、4、5；5、12、13；7、24、25；9、180、181；……。它们整体互素，且有两个为连续的正整数。这些解也被称之为本原勾股数。它们可以通过公式：a=2n+1、b=2n2+2n、c=2n2+2n+1得到。显见，具有这些性质的勾股数有无穷多个。人们把满足不定方程x2+y2+z2=w2且互素的正整数解称之为3维本原勾股数。我们不禁会想3维本原勾股数也有类似的奇妙现象吗？对应这样的解有多少个？怎样求出对应的解呢？笔者试就以上问题作一些探索。

2 具有三个连续正整数的3维本原勾股数的解

由于3维本原勾股数是由四个数组成，设为a、b、c、d，且(a、b、c、d)=1，其中必然有两个为偶数两个为奇数，其中最大的一个数d一定是奇数[1]，若a、b、c、d四个数是连续正整数，只能是a=2n、b=2n+1、c=2n+2、d=2n+3，则有

(2n)2+(2n+1)2+(2n+2)2=(2n+3)2

所以，至多只能有三个连续的整数。

定理1：设a、b、c、d是本原3 维勾股数，其中含有三个连续的正整数的只有1、2、2、3唯一的一组解。

证：若a、b、c为连续的整数，因为其中有两个偶数一个奇数，分别设为a=2n+1、b=2n、c=2n+2，若存在奇数d=2m+1使得a2+b2+c2=d2，则有

(2n+1)2+(2n)2+(2n+2)2=(2m+1)2

于是有

3n(n+1)+1=m(m+1)

上式中，左边是奇数而右边为偶数，显然不能成立。故a、b、c不能成为连续的整数。

若a、b、d为连续的整数，因为其中有两个奇数一个偶数，分别设为a=2n-1、b=2n、d=2n+1代入a2+b2+c2=d2有

(2n-1)2+(2n)2+c2=(2n+1)2

于是有

c2=4-4(n-1)2

由于a、b、c、d都是正整数，只有n=1，即只有1、2、2、3唯一的一组解。

3 具有两对连续正整数的3维本原勾股数及其算法

对于不定方程x2+y2+z2=w2具有两对连续整数的3维本原勾股数解的问题，我们有如下的结论：

定理2：设a、b、c、d是本原3维勾股数，当a、b为两个连续整数，则c、d也是连续整数的充分且必要条件是c=ab。

证：若b=a+1，d=c+1为两对连续正整数，代入a2+b2+c2=d2有

a2+(a+1)2+c2=(c+1)2

展开化简，即得

c=a(a+1)=ab

若

b=a+1,c=ab=a(a+1)

那么

a2+(a+1)2+[a(a+1)]2=a4+2a3+3a2+2a+1=(a2+a+1)2

即

d=a2+a+1=a(a+1)+1=c+1

c、d也是连续整数。

根据以上的结论，可构造计算公式，并计算结果如下：

令a=nb=n+1c=n(n+1)d=n(n+1)+1ìîíïïïï可得abcd12232367341213452021563031674243…………

满足以上性质的3维本原勾股数都可以由唯一的参数a的取值而随之确定。显然，a可以取任何正整数，对于一个确定a的值有且仅有一组解。

4 具有一对连续正整数的3维本原勾股数的求解问题

假设a2+b2+c2=d2中c=d-1，我们观察一下a、b、c、d有什么关系。

由于

d2-c2=d2-(d-1)2=2d-1

若2d-1=a2+b2有整数解，即已经得到问题的答案。

当2d-1为模4余1的素数时，显然成立[2]128。

如：d=7,2d-1=13为模4余1的素数，对应有解3、2、6、7；

d=9,2d-1=17为模4余1的素数，对应有解1、4、8、9；

当2d-1含有4x-1的素数(即：模4余3的素数)时，2d-1不能表示成a2+b2形式[3]113，也就是说找不到具有以上性质的解。

如：d=5, 2d-1=9=32，因为9不是素数，而3是模4余3的素数，则不存在正整数a、b使a、b、4、5为勾股数。

对于d=11,2d-1=21=3×7，3和7都是模4余3的素数，也不存在正整数a、b使a、b、10、11为3维勾股数。综上所述，我们得到以下结论。

定理3：对于奇数d，存在一组正整数a、b、c、d是本原3维勾股数，且c、d为连续整数的充分必要条件是2d-1为模4余1的素数。

如果2d-1不是素数，而是若干个素数的乘积，设2d-1=p1p2…prM2，其中p1、p2…pr是互不相同的素因子，则2d-1可以表示成两个平方数之和的充要条件是，每一个pi为模4余1的素数[2]128。这表明只要2d-1中除平方因子外不含有模4余3的素因子，则对于奇数d，存在正整数a、b使得a、b、d-1、d是本原3维勾股数。

比如d=33,2d-1=65=5×13，5和13都为模4余1的素数，对应有

2d-1=5×13=(12+22)(22+32)

作如下变式

即可得到a=7、b=4、c=32、d=33为一组具有两个连续正整数的3维本原勾股数。

接下来的问题是，这样的本原3维勾股数有多少个呢？

定理4：对于奇数d，若2d-1=p1p2…prM2，且p1、p2…pr是互不相同的模4余1的素因子，则存在正整数a、b使得a、b、d-1、d是本原3维勾股数的个数有2r-1个(r是模4余1的素因子的个数)。

证(数学归纳法)：当r=1时2d-1=p1M2，根据参考文献[3]109结论

p1=a12+b12

那么

2d-1=(a12+b12)M2=(a1M)2+(b1M)2

取a=a1M、b=b1M得a、b、d-1、d是一组本原3维勾股数，且是唯一的一组解。

结论成立。

假设r=k时结论成立，

当r=k+1时，2d-1=p1p2…pk+1M2；根据归纳假设，对于p1p2…pkM2有2k-1组不同的正整数Ai、Bi(i=1,2,3,…,2k-1)的值，使得p1p2…pkM2=Ai2+Bi2；

又pk+1是模4余1的素数，因此pk+1=ak+12+bk+12

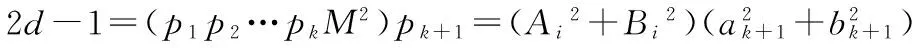
而

=(Aiak+1-Bibk+1)2+(Aibk+1+Biak+1)2

或

=(Aiak+1+Bibk+1)2+(Aibk+1-Biak+1)2

i=1,2,3,…,2k-1

所以，对于2d-1=p1p2…pk+1M2，存在2k-1×2=2(k+1)-1组不同的正整数Si、Ti的值，使得2d-1=p1p2…pk+1M2=Si2+Ti2；

即r=k+1时结论成立。

根据数学归纳法原理，该结论对一切正整数r成立。

例如：d=553,2d-1=1105=5×13×17，符合条件的解应有4组。它们可以通过如下方式求得：

则

=92+322

=232+242

=312+122

=332+42

从而得到9、32、552、553；23、24、552、553；31、12、552、553；33、4、552、553四组具有一对连续正整数的本原3维勾股数。

5 结语

二维勾股数中具有许多奇妙的性质，与之对应三维勾股数也有相应的性质。但由于维数的增加，其对应的性质是大不相同的，变得更加复杂和奇妙。笔者在这里探索了有连续正整数的3维本原勾股数解的条件和求解的方法及其解的个数，并以行列式的计算形式给出了构造有两个连续正整数的3维本原三维勾股数的计算范例。

[1]颜有祥.三维勾股数的性质及其计算方法[J].新乡学院学报：自然科学版，2010，(3).

[2][美]Joseph H.Silverman.数论概论[M].孙智伟，等，译.北京：机械工业出版社，2008.

[3]闽嗣鹤，严士键.初等数论(第三版)[M].北京：高等教育出版社，2003.