一种高效智能的参数化设计方法

胡 宗 政

(兰州职业技术学院，兰州 730070)

随着CAD/CAM/CAE技术的不断发展，参数化设计的建模技术在各行各业已经得到了广泛应用。所谓参数化设计就是指采用一组相关参数来映射产品的几何特征，建立模型几何尺寸与参数的对应关系，通过参数的设置和编辑，快速修改和控制几何形状，自动实现模型的精确造型，快捷高效地完成一系列相似形状的模型的重新设计。Pro/E软件作为一款参数化设计的典型应用软件，整合了包括CAD/CAM/CAE技术在内的很多应用模块，其行为特征建模技术将CAE技术与CAD建模融于一体，通过定义分析特征，驱动参数模型，自动修改模型特征参数，实现设计过程的目标驱动。

本文综合利用Pro/E软件的行为特征建模技术，借助MathCAD软件强大的计算功能和简洁的数据优化功能，通过MathCAD和Pro/E之间的数据传输，完成了渐开线直齿圆柱齿轮的参数化优化设计，阐述了Pro/E行为特征建模的基本过程与步骤。

1 齿轮参数化建模

1.1 建模思路

1.2 优化设计思路

软齿面齿轮传动具有制造方便、成本低等优点。在对精度、强度和速度要求不高、传动功率较低、对齿轮尺寸无严格限制环境下得到了广泛的应用。

本文在综合考虑软齿面齿轮性能要求以及工作条件的基础上，确定齿轮中心距最小为优化目标，利用MathCAD中Minimize函数获得符合优化目标的各齿轮模数、齿数等基本参数的初始值，从而确定齿轮系统所有几何参数。

2 齿轮参数优化数学模型的创建

2.1 目标函数与设计变量

假设以齿轮传动系统中心距最小为优化目标，则目标函数可写为：

(1)

式中：m1、m2为高、低速齿轮模数；z1、z2为高、低速小齿轮的齿数；i1为高速级传动比；i为总传动比。

由式(1)可知,齿轮传动的总中心距a与模数m1、m2,小齿轮齿数z1、z2,第一级传动比i1,齿宽系数φd1、φd2的取值有关,所以选择这几个参数作为独立的设计变量,即:

x=(m1,m2,z1,z3,φd1,φd2,i1)

=(x1,x2,x3,x4,x5,x6,x7)

(1)

2.2 约束条件分析

(1)齿面接触强度约束条件。

接触应力为脉动循环交变应力,齿面接触强度的约束为:

(2)

式中：K1=KA1KV1Kα1Kβ1，d1=m1z1，[σH]为许用接触应力；ZH为节点区域系数；ZE为材料弹性模量；KA为使用系数；KV为动载系数；Kα为齿间载荷分配系数；Kβ为齿向载荷分配系数；T1为高速级传递的转矩。

(3)

式中：K2=KA2KV2Kα2Kβ2，d2=m2z2，T2为低速级传递的转矩，其余参数同上。

(2)齿根弯曲强度约束条件。

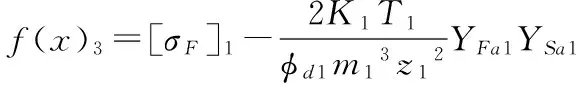
(4)

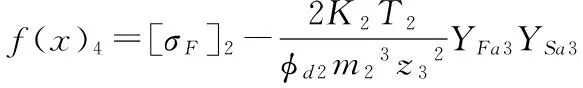
(5)

式中，[σF]为许用齿根弯曲强度；YFa为齿形系数；YSa为应力校正系数。

(3)模数的约束。

对于动力传动齿轮，一般要求模数大于2mm，约束条件可以表述为：

f(x)5=m1-2≥0

(6)

f(x)6=m2-2≥0

(7)

(4)小齿轮齿数约束。

对于压力角为20°的标准直齿圆柱齿轮，为了避免根切，齿数应该大于17：

f(x)7=z1-17≥0

(8)

f(x)8=z3-17≥0

(9)

(5)齿宽系数的选择。

对于标准圆柱齿轮传动,通常要求：0.8≤φd≤1.4，因而有：

f(x)9=φd1-0.8≥0

(10)

f(x)10=1.4-φd1≥0

(11)

f(x)11=φd2-0.8≥0

(12)

f(x)12=1.4-φd2≥0

(13)

2.3 利用MathCAD分析进行优化设计

通过调用MathCAD中maximize、minimize二个函数可以求得目标函数的最大值和最小值。工作步骤如图1所示。

3 MathCAD优化分析

MathCAD是美国PTC公司所属的一款集数理计算、图形和文字处理等功能于一体的工程计算软件，能够进行强大的计算和分析，很好地弥补了Pro/E软件在计算方面的不足。

(1)Pro/E中MathCAD分析的工作流程，见图2。

现要求设计一个二级展开式减速器。已知高速轴输入功率P1=6.2kW,高速轴转速n1=960r/min,总传动比i=15,由电动机驱动,工作寿命15年(设每年工作300天),二班制,大齿轮45钢正火HB187～207,小齿轮45钢调质HB228～255,带式输送机工作平稳,转向不变。要求按总中心距最小来确定总体方案中各齿轮的主要参数。

(2)新建Pro/E装配文件，按照任意中心距装配二级齿轮，装配约束类型为销钉连接方式，如图3(a)所示。在Pro/E中新建一个参数ZD=1，用于Pro/E传送给MathCAD进行计算。

(3)单击主菜单“分析”→“外部分析”→“MathCAD分析”。在弹出的对话框中单击“新文件”按钮，打开MathCAD软件，单击“文件”→“新建”，新建MathCAD文档，并建立优化数学模型，进行计算，最后求得各齿轮的模数、齿数、分度圆直径、齿宽等几何参数。(计算步骤有省略)。

f(x1,x2,x3,x4,x5,x6,x7)

x1∶=2x2∶=3x3∶=19x4∶=19x5∶=1x6∶=1x7∶=6.7

已知

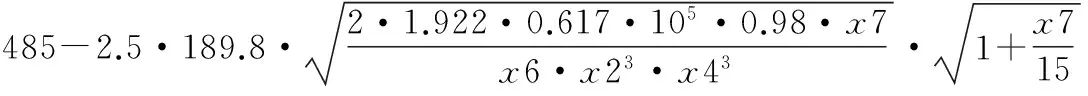
x1-2≥0

x2-2≥0

……

1.4-x6≥0

Minimize(f,x1,x2,x3,x4,x5,x6,x7)

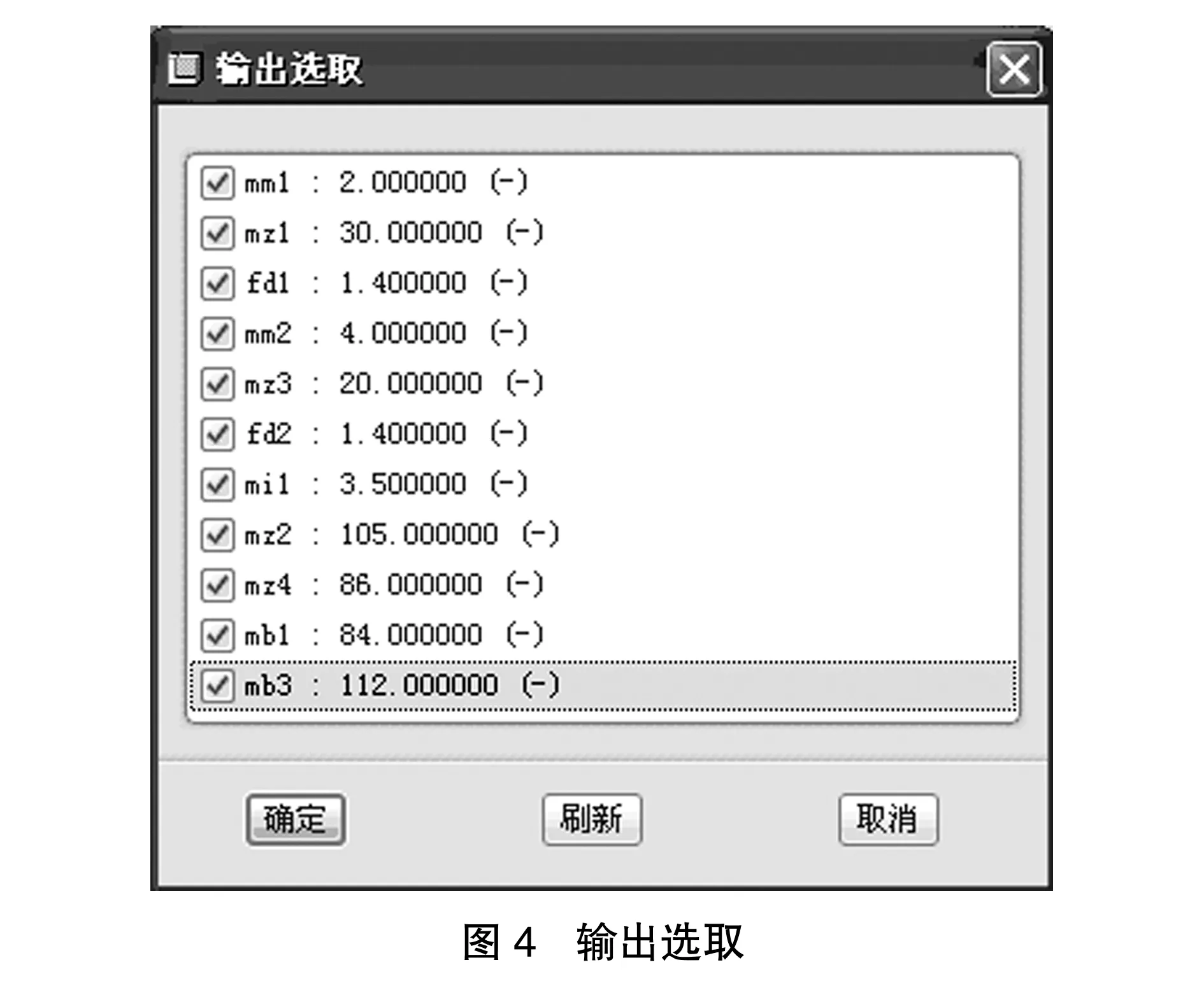
圆整后得到结果：mm1=2、mz1=30、fd1=1.4、mm2=4、mz3=20、fd2=1.4、mi1=3.5

(4)声明变量。

在MathCAD分析过程中，用到的变量有的是从Pro/E输入到MathCAD的，有的是从MathCAD输出到Pro/E的。为了完成数据传送，需要为变量定义一个标签。选中一个变量的定义式，点击右键→“属性”，然后在“显示”选项卡中找到“标签”并输入“proe2mc”或“mc2proe”。在此例中，Z1需要添加第一种标签，mm1、mm2、mz1、mz3等需要返回到Pro/E的参数需要添加第二种标签。完成后保存文件为“gear.xmcd”。

(5)单击“加载文件”按钮，在打开的文件浏览窗口选择刚刚新建的“gear.xmcd”文件。单击“添加参数”在弹出的“参数选取”对话框中选择Pro/E中设定的参数，单击“确定”后在“输入选取”对话框中选择MathCAD中对应参数。

(6)输出MathCAD变量到Pro/E中。单击“输出”，在弹出的“输出选取”对话框中选则需要输出到的Pro/E中的参数，比如大小齿轮的模数、齿数、齿宽等，以便于后续计算，如图4所示。

(7)依次单击“计算”→“添加特征”，并为分析命名。单击“关闭”，完成分析特征的创建，在这个特征中自动建立了结果参数。

(8)在Pro/E中添加关系。

为了将MathCAD中输出的模数、齿数、齿宽等数值再次附值给Pro/E中的对应值，实现模型同步更新，需要在Pro/E中添加相应的关系式，比如：

M:2=MC_MM1:FID_ANALYSIS1

Z:2=MC_MZ1:FID_ANALYSIS1

B:2=MC_MB1:FID_ANALYSIS1

Z:4=MC_MZ2:FID_ANALYSIS1

M:4=MC_MM1:FID_ANALYSIS1

B:4=B:2+5

d0=(M:2*Z:2+M:4*Z:4)/2

Z:6=MC_MZ3:FID_ANALYSIS1

M:6=MC_MM2:FID_ANALYSIS1

B:6=MC_MB3:FID_ANALYSIS1

Z:8=MC_MZ4:FID_ANALYSIS1

M:8=MC_MM2:FID_ANALYSIS1

(9)修改Pro/E中相关参数的数值，再生模型，MathCAD自动计算出来的结果也会动态变化，在MathCAD中数据的更新，传输到Pro/E中后再生模型，特征几何参数同步变化，这样就实现了MathCAD和PRO/E之间数据的传输、计算和同步更新，即如果如图3(b)所示。

4 结语

传统设计中，对于多级展开式齿轮传动系统的设计，一方面计算复杂，容易出错，另一方面无法对传动系外轮廓尺寸、体积、重量以及制造成本等进行优化。本文借助于Pro/E与MathCAD软件集成解决方案，在Pro/E环境中实现了以轮廓尺寸最小为目的的齿轮传动系统的参数最优化设计，实现了优化结果与实体模型的同步更新，不仅充分发挥了Pro/E在机械设计中的参数化造型优势，而且结合了MathCAD的强大工程计算能力，提高了工程技术及优化设计的能力。设计方法高效、智能、简单易行,具有一定的实用价值和推广价值。

[1]刘洁，王德俊，姚志英.齿轮传动的优化设计[J].煤矿机械，2006，27(7)：27～28.

[2]贾吉林.基于Pro/E斜齿圆柱齿轮参数化设计及运动仿真[J].煤矿机械，2010，31(7)：230～232.

[3]庞爱民，生鸿飞，王震国.基于参数化建模的Pro/E齿轮设计[J].湖北民族学院学报：自然科学版，2007，25(3)：298～300.

[4]马本学，彭春雷，刘银，葛建兵，过健.MathCAD在齿轮参数优化设计中的应用[J].石河子大学学报：自然科学版，2006，24(6)：759～760.

[5]朱学文，朱国文，何小新.斜齿轮的参数化建模与动力学分析[J].机械传动，2006，30(2)：32～33.

[6]濮良贵，纪名刚.机械设计[M].北京：高等教育出版社，1996.