超导体二硼化镁电子结构和掺杂研究

刘 洋

(孝感学院 化学与材料科学学院，湖北 孝感 432000)

超导体，顾名思义就是通电流后没有能量耗散的导体.它是由于大量配对电子凝结到一个“布调一致”的相干态后，其运动不受晶格散射的结果.1911年，荷兰的科学家Onnes发现水银的超导现象后，人们一直期望能找到室温超导体，这是人们长期以来的梦想.氧化物超导体的超导机制是物理学家面前的最富有意义和挑战性的课题之一.这是由于此类材料中电子之间的相互作用很强，其运动行为似乎不能用业已成熟的固体物理的知识来理解.对高温超导机理的理解可能会导致人们对很多被称为电子强关联的一大类材料物理本质的理解，同时在科学和技术两个方面产生飞跃.

2001年1月MgB2的超导电性被发现以来[1],这种临界温度高达39 K的简单二元合金超导体引起了人们的强烈关注,短时间内就对其进行了深入、广泛的研究.首先，人们发现，这个超导体在20 K左右的温度和8万倍于地球磁场的情况下，可以承载很大的超导电流，而且能耗极低.由于20 K的温度可以方便地使用小型制冷机获得，因此这使得人们想到在将来的医院里使用的核磁成像仪器的超导磁体再也不要昂贵的液氦来运行，而只需要插上电源就行了.另外，二硼化镁材料的价格很低，而且远比陶瓷特性的氧化物高温超导体容易加工成型，因此在发现后不久，美国Ames实验室就能够拉出长达几十米的线材和带材.此外，二硼化镁超导体的超导相干长度较长，容易制备出超导量子干涉器件用于微弱电磁信号的检测，在大地探矿、医疗仪器、环境和军事方面具有应用前景.

利用基于密度泛函理论(DFT)的线性缀加平面波方法(LAPW)对多频带双能隙超导体二硼化镁进行电子结构研究，并对其进行电子掺杂和空穴掺杂的计算，在掺杂计算中用铝原子代替镁原子，碳原子代替硼原子.二硼化镁在费米面形成四条能带，其中两条是σ带，主要由硼的px+py分量形成，另外两条是π带，主要由硼的pz分量形成，σ带对超导性起主要作用.在二硼化镁超导体中，镁原子能够被铝和钪取代形成Mg1-xAlxB2和Mg1-xScxB2，硼能够被碳取代形成Mg(B1-yCy)2.在这些情况中用来替代的原子在原子实外都包含不止一个电子.如铝为Al：3s23p1；Sc：4s23d1；C：2s22p2.实验显示，无论在哪种替代下，二硼化镁的超导临界温度Tc都会下降.笔者发现不管是哪种掺杂临界温度Tc的下降都和能带的饱和情况和带间散射有关，当这些替代原子的外层电子占据了σ带，使这些带变得饱和时，材料的超导性就下降了.

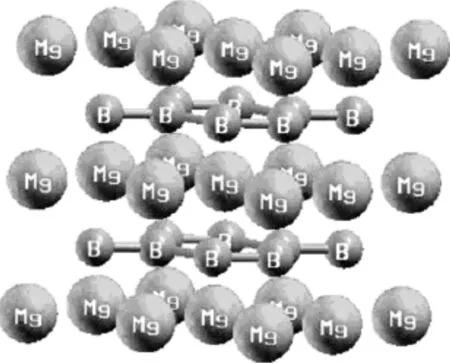
图1 MgB2的原子结构图Fig.1 The atomic structure of MgB2

atomxyzMg000B1/32/33/3B-1/32/31/2

(P6/mmm，lattice a=b=3.086 Å，>c=3.522 Å)

1 二硼化镁电子结构和掺杂研究

二硼化镁具有超导电性，是高温超导界中结构最为简单的一种合金，因此，科学家们对这种物质进行了深入的研究，其中包括理论计算[2-10]和实验[11-16].这些研究包括如何提高二硼化镁的超导临界温度，探讨二硼化镁的根本超导机制.理论计算和实验结果都表明，二硼化镁是以声子为媒介的BCS超导体其超导电性源于硼原子的声子谱，掺杂能够极大的提高二硼化镁的临界超导温度.二硼化镁的结构属六方晶系(如图1)，在两个硼原子层之间有一个镁原子层.各地的实验小组用不同的实验方法和技术发现了二硼化镁许多特别的，不寻常的甚至与超导机制相矛盾的性质.Louie和Cohen的小组用完善的BCS理论研究了二硼化镁的基本性质，Choi发展了复杂电子结构材料的BCS方程的解法，他们用来解决二硼化镁的基本性质.文献报导了从头计算方法计算的超导能隙和它引起的可观测量[17].一个重要的特征是硼原子与某种特定的声子模式形成强烈的耦合，电子态密度被这样的硼原子轨道占据，有助于电子对的形成.这解释了二硼化镁的高超导临界温度，反常的热学现象和多能隙结构.

对二硼化镁的电子结构进行研究，包括它的电子能带图、态密度(DOS)和电荷密度，利用基于密度泛函理论(DFT)的线性缀加平面波方法(LAPW)，使用的程序包是WIEN2K[18].这种方法能够在其它缀加平面波的基础上对局域轨道进行计算，这样便提高了计算的线性化，同时使在一个能量窗口内同时对内层电子和价电子进行计算成为可能.但是这种方法也存在着的近似，首先，晶胞被划分为两个部分：以原子位置为中心的非重叠Muffin-tin球区域和球间区域.其次，晶体势也相应的分为两个部分：

V(r)=∑Vlm(r)Ylm(θ,Ф) (球内)

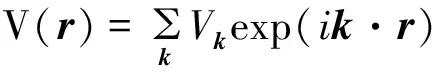
其中Ylm(θ,Ф)为球谐函数，因此必须要设定控制参数.采用实验给出的数据[19，20](见表1).

马玲球半径分别取Mg：2.0，B：1.5.(对此实验数据进行了优化，实验上测得的数值和优化所得到的数值吻合的非常好)故在计算中使用实验数据.第一布里渊区中k点的个数取为100，控制基函数集大小的收敛参数RKmax=8.

图2、3和图4给出了二硼化镁的能带、态密度和费米面的电荷密度分布图.计算的二硼化镁的能带图能量从-15 eV至10 eV，费米面取零.

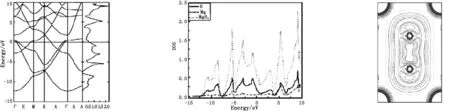
图2 二硼化镁的能带分布图 图3 二硼化镁的态密度分布图 图4 二硼化镁的费米面电荷密度分布图Fig. .3 The profile of states density distribution of MgB2 Fig. .4 The profile of charge density distribution in Fermi surface of MgB2

可以看见有四条能带穿越了费米面，显示了二硼化镁的导电性.穿过费米面的这四条能带主要来源于哪个原子，那么此种原子就对二硼化镁的超导性起主要作用.为了研究这个问题，笔者分别画出了各个原子轨道的能带特征图，经过对比发现穿过费米面的这四条能带来自硼原子的p轨道.图5所示，图中圆圈半径的大小代表此原子轨道对能带形成贡献的大小.图5中的(a)是硼原子的p轨道的能带特征图，可以看出硼原子位于p轨道的电子对于导带和穿过费米面的这四条能带贡献很大，为了对比也计算了硼的s轨道、镁的s和p轨道的能带特征图，确定穿过费米面的这四条能带主要来自硼原子的p轨道.其中两条来自px+py轨道，另外两条来自pz轨道.图5(b)和图5(c)显示.费米面以上的导带则主要源于镁的最外层自由电子和部分硼的p轨道电子.这点也可以从图4中得到证实，图4是二硼化镁在费米面的电荷密度分布图，正中间的是两个硼原子，边上的是镁原子.图4中显示，硼原子和硼原子之间有很强的相互作用，而硼原子和镁原子之间的相互作用很弱，镁原子基本处于电离状态.镁原子的外层电子势必对导带起较大贡献.图2中与能带图相对应的是总态密度，注意到在费米面态密度较小，由图3得知零点能的态密度主要来自硼，图5(d)更清楚地看出硼的p轨道电子及pxy和pz轨道态密度的值.pxy的态密度比pz的高出许多，从图5的(a)(b)(c)可以看到pxy能带穿越费米面四次而pz只穿越两次.从以上的计算和分析肯定了硼原子在超导中起的关键作用.

硼化镁是一种结构简单易于加工的合金，为了寻求临界温度更高的超导体，许多实验小组对二硼化镁进行了掺杂.在这里笔者用构建超元胞的方法对二硼化镁进行碳掺杂和铝掺杂的研究.

二硼化铝没有超导性，为了比较，笔者计算了二硼化铝的电子结构.二硼化铝的结构参数由实验给出：a=b=2.868 2Å，c=3.11Å.经过优化验算，得出实验给出的参数是使二硼化铝处于稳定能量最低的值，所以计算采用实验得出的结构参数.铝的性质介于金属和非金属之间，所以硼和铝形成的化学键既有可能是离子键也有可能是共价键.经过优化计算比较，笔者发现化学键的形成和铝和硼原子之间的距离有关系，当硼铝原子之间的距离大于2.97时，硼和铝原子之间就是离子键，当距离小于2.96，就形成共价键.也就是说，当硼铝之间的距离足够长的时候，硼和铝之间在不会共享任何电子.当距离缩短到某一个范围的时候，硼铝的电子云就会形成交叠.根据优化得到的结果，使二硼化铝处于稳定状态的结构是硼铝都处于离子状态的结构.因此，在计算中，硼铝也形成离子键.

在二硼化镁中掺入适当的铝，形成Mg1-xAlxB2的分子，其中的x代表铝的含量.掺杂时铝的替代位置有八种，分别是(0，0，0)，(0.5，0，0)，(0，0.5，0)，(0.5，0.5，0)，(0，0，0.5)，(0.5，0，0.5)，(0，0.5，0.5),(0.5,0.5,0.5).这些位置当中，(0，0，0)是掺杂位置最简单的，(0，0，0.5)是掺杂以后能量最低的.所以在进行掺杂计算时，笔者尽量采用这些位置进行替代.

分别使x=0.062 5，0.125，0.25，0.375，0.50，0.625，0.75和0.875.在x=0.062 5时，铝占的态密度很小，态密度曲线几乎和二硼化镁没有什么区别，增大掺杂浓度，x=0.125和x=0.25时，铝所占的态密度仍然很小，不能仅从态密度判断出铝和硼，实验表明，在掺杂浓度不太大时，二硼化镁的超导性会下降，但它仍是超导体.当掺杂的浓度继续升高，铝占据的态密度比例增大，而硼和镁的态密度比例下降，x=0.375时，铝的态密度会线性迅速增长，这时复合物很快的失去超导性.从对二硼化镁的分析可以看到，超导性源于硼原子的pxy轨道电子.在掺入铝原子后，铝比镁多一个电子，这样它势必会破坏原来的电-声相互作用，从能带图(图6)中可以看到，掺入铝之后，原来pxy轨道发生了变化，这在k点很明显，带间的散射增强了.原来的pxy轨道的能带变得更加倾斜，这是铝的电子填充了pz轨道导致.

图6 MgB2掺铝能带图Fig.6 The energy band diagram of MgB2 after incorporating Al

接下来，在二硼化镁中掺入了碳元素，掺杂物的化合式可表达为Mg(B1-yCy)2.构建了一个2×2×2的超元胞，用碳原子取代化合物中的硼原子，取代的比例分别为y=0.25和y=0.50.为了减少计算的时间，利用了晶体结构的对称性和一些近似.在计算过程中，k点取100，对掺杂物进行了体积优化，对y=0.25的情况，最低的优化能量为726 eV，比实际计算能量低2%，而对于y=0.50的情况，优化的能量基本等于计算的能量.所以在实际计算中，采用实验给出的晶胞参数，没有采用优化数据作计算.实验给出的晶胞参数在表1中详细列出.

计算的超元胞的DOS图和能带结构图如下(图7-图10).从图中可以看出，对于y=0.25的情况，对应于图7，在总的态密度中，碳占的比重不大，总的态密度在费米面处的贡献主要来源于硼原子，据实验报导，在二硼化镁中掺入25%碳元素时，二硼化镁掺杂物仍有微弱的导电性，从能带结构图中看出，在费米面仍有一些能带穿越，能带结构图与原来二硼化镁的结构图有几分相似，有导电的自由电子存在.对比y=0.50的情况可以明显看到，在总的态密度中，费米能处的态密度主要贡献是碳原子，此时硼原子的贡献处于次要的地位，而且y=0.50的能带图也可以看出，与原来二硼化镁的能带图差异大，看不到明显表示自由电子的能带穿越费米面.同时，实验结果证明y=0.50时二硼化镁的掺杂物已经完全失去了超导性.

图7 y=0.25时超元胞的DOS图 图8 y=0.5时超元胞的DOS图Fig.7 when y=0.25，the super cell DOS map Fig.8 when y=0.5，the super cell DOS map

图9 y=0.25时能带结构图 图10 y=0.5时能带结构图Fig.9 when y=0.25，the energy band diagram Fig.10 when y=0.5，the energy band diagram

2 结论

对MgB2超导体进行了第一性原理的计算，采用构建超元胞的方法对MgB2进行碳掺杂和铝掺杂的研究.计算分析了MgB2的能带结构、态密度、费米面的电荷密度并与掺杂以后的图形进行对比，验证二硼化镁的超导性主要来源于硼原子，穿过费米面的四条能带都是硼原子的，其中两条是σ带，来自px+py电子轨道，另外两条是π带来自pz轨道.对二硼化镁构建超元胞进行掺杂以后，掺杂原子碳、铝的外层电子占据了σ带，使能带变得较以前饱和，降低二硼化镁的超导性.这与实验得出的结果一致.

[1] Nagamasu J,Nakagawa J,Muranaka T,et al.Akimitsu.Superconductivity and its applications[J].Nature,2001,410:63-67.

[2] Nagamatsu Jun,Nakagaws Norimasa,Muranaka Takahiro,et al.Superconductivity and its applications[J].Nature,2001,410:63-75.

[3] Budko S L,Petrovic C,Lapertot Getal.The properties of granular superconducting MgB2[J].Phys Rev Lett,2001,86:11 402-11 406.

[4] Liu A Y,Mazin I I,Kortus J.Influence of Pressure on the Superconductivity of MgB2[J].Phys Rev Lett,2001,87:87 005-87 007.

[5] Finnemore D K,Ostenson J E,Bud’ko S L,et al.The relationship between the superconductivity of doping MgB2and the number of average valence electrons[J].Phys Rev Lett,2001,86:2 420-2 431.

[6] Dreizler R M,Gross E KU.Density Functional Theory[M].Berlin Heidelberg:Spinger-Verlag,1990:1-47.

[7] 谢希德,陆栋.固体能带理论[M].上海:复旦大学出版社:1998:14-269.

[8] Nagy A.The new superconductor MgB2and its applications[J].Physics Reports,1998,298:1-79.

[9] Franci M.The research of lattice parameter of the doping MgB2series and the doping choice of MgB2[J].Chemical Physics Letters,1996,263(13):506-514.

[10] Glossman M.Doping properties of MgB2superconductor[J].Daniel Journal of Molecular Structure,1997,390:67-69.

[11] Osborn R,Goremychkin E A,Kolesnikov A I,et al.Isotope effect of MgB2superconductor[J].Phys Rev Lett,2001,7:17 005-17 008.

[12] WeiKu,Pickett W E,Scalettar R T.Research and progress in magnesium diboride superconductor[J].Phys Rev Lett,2002,88:57 001-57 005.

[13] Canfield P C,Finnemore D K,Bud′ko SL.The superconductivity and doping effect of MgB2[J].Phys Rev Lett,2001,86:2 423-2 426.

[14] Finnemore D K,Ostenson J E,Bud′ko,SL,et al.Penetration-depth anisotropy in MgB2:two-band ginzburg-landau theory[J].Phys Rev Lett,2001,86:2 420-2 422.

[15] Bud′ko S L,Lapertot G,Petrovic C,et al.The two-band ginzburg-landau theory based analysis on the gaps of the superconductor MgB2[J].Phys Rev Lett,2001,86:1 877-1 880.

[16] Amy Y Liu,Mazin I I,Jens Kortus.Study on the transport properties of superconductor MgB2[J].Phys Rev Lett,2001,87:87 005-87 009.

[17] Choi Hyoung Joon Roundy,David Sun,Hong,et al.The relation of energy gaps between specific heat for MgB2superconductor[J].Nature,2002,418:758-762.

[18] Blaha P,Schwartz K,Madsen G,et al.Computercode WIEN2K[M].Wien:Technische Universitat Wien，1999:45-76.

[19] Wyckoff R W G.Crystal Structure[M].New York:Wiley,1995:25-67.

[20] An J M,Pickett W E.Improving critical current density of MgB2by codoping with c and al[J].Phys Rev Lett,2001,86:4 366-4 371.