原子净电荷分布对乙烯基类单体聚合机理的判定

谭 姚，李世荣，聂光华，田大听

(湖北民族学院 化学与环境工程学院，湖北 恩施 445000)

近年来许多理论研究表明，采用密度泛函理论(Density functional theory,DFT)的方法来研究化合物，能较好地解释一些化合物的电子性质及磁学性质[1].DFT是一种研究多电子体系电子结构的量子力学方法.因密度泛函理论方法不仅考虑了电子相关，而且节省机时，计算结果较好，所以广泛应用于研究各种化合物[2].众所周知，在乙烯基类单体中,因其碳-碳双键既可均裂，也可异裂.因此，其聚合反应机理既可是自由基聚合又可是离子聚合.由于取代基团能改变双键的电子云密度，并对乙烯基类单体中碳-碳原子之间的净电荷分布产生影响.所以当碳-碳双键两边对称或者其原子净电荷之差较小时，如乙烯，则发生自由基聚合反应.而当碳-碳双键原子之间净电荷之差较大时，如：烷氧基、硝基等，其碳-碳双键电子云密度变化较大，则发生离子聚合反应[3].而有些取代基，虽使碳-碳原子之间的净电荷之差适中，但由于共轭作用，其电子流动性较大，而使分子三种聚合机理都可能发生.文献检索表明，用DFT来研究聚合机理的较少.正是由于DFT可以计算化合物的净电荷分布，因此可以通过计算不同种类的乙烯基类单体的净电荷分布，就可以提供一种新且简单的判定乙烯基类单体聚合机理的方法或判据.

1 计算方法

本研究选择了能较好处理电子相关问题的密度泛函理论DFT-B3LYP方法，结合6-31d基组，计算了乙烯基类单体分子的几何构型及原子净电荷分布.从理论上探讨了乙烯基类单体聚合机理的方法或判据[4].根据计算净电荷之差Δe=|e1-e2|(e1表示碳-碳双键上的一个碳原子上的净电荷，e2表示碳-碳双键上的另一个碳原子上的净电荷)，并判断其聚合反应机理.所有的计算都使用Gaussian03[5]密度泛函理论(DFT)方法.分子几何构型和原子净电荷分布图使用Gauss View得到.

2 结果与讨论

2.1 净电荷差较小(Δe<0.1)的乙烯基单体的几何构型及净电荷分布

当净电荷之差较小时(Δe<0.1)，对CH2=CH2和CH2=CHCl单体分子构型进行了分析.图1是由Gaussian03密度泛函理论(DFT)方法得到的CH2=CH2单体分子的几何构型和其原子净电荷分布情况，可以看出碳-碳原子之间的净电荷之差Δe为零.说明分子电荷分布很均匀，当链引发时，极易形成自由基，而当自由基一旦生成，便会立即与其它的自由基反应，生成含有两个至多个的单体单元的乙烯基链自由基，而链自由基的聚合度就这样迅速增加，并最终发生了自由基聚合反应.如图2是由同样的方法得到的CH2=CHCl单体分子的几何构型和其原子净电荷分布情况，可以清楚的发现碳-碳原子之间的净电荷之差较小Δe=0.09.图2是由于氯原子有吸电子作用(即诱导效应)，且吸电子作用不强，导致碳-碳双键之间的净电荷较小且分子电荷分布较均匀.当发生反应时，就较容易形成其自由基，而不容易形成离子，从而最终发生自由基聚合反应.

由图1,2可得：当原子净电荷之差较小时(Δe<0.10)，乙烯类单体聚合机理为自由基聚合.

图1 CH2=CH2分子的几何构型及净电荷分布 图2 CH2=CHCl分子的几何构型及净电荷分布Fig. .1 The geometrical configuration and the distribution of the atomic net charge of CH2=CH2 Fig. .2 The geometrical configuration and the distribution of the atomic net charge of CH2=CHCl

2.2 净电荷之差较大(Δe>0.35)荷分布

当净电荷之差较大时(Δe>0.35),选择了四个化合物的分子构型进行了分析.首先，选择CH2=CF2和CH2=CFCF3的分子构型进行了分析.图3由Gaussian03密度泛函理论(DFT)方法得到的CH2=CF2单体分子的几何构型和原子净电荷分布情况，可以发现碳-碳之间的净电荷之差较大Δe=1.03，因其净电荷之差较大，导致分子的电荷分布不均匀.图3是由于两个氟的强吸电子作用(即诱导效应)，使碳-碳之间π键的电子分布发生较大的偏移，碳-碳π键只能发生异裂.当链引发时，产生阴离子基，从而只能发生阴离子聚合反应.图4是由同样的方法得到的CH2=CFCF3单体分子的几何构型和原子净电荷分布情况，可以发现碳-碳之间的净电荷之差较大Δe=0.73，因三氟烷基和氟离子是强吸电子的基团(即诱导效应)，使碳-碳之间π键的电子分布发生较大的偏移，导致原子的电荷分布不均匀，则碳-碳π键断裂时只能发生异裂，从而只能发生阴离子聚合反应.其次，选择CH2=C(CH3)2和CH2=CHOCH3的分子构型进行了分析.图5由Gaussian03密度泛函理论(DFT)方法得到的CH2=C(CH3)2单体分子的几何构型和原子净电荷分布情况.可以发现其净电荷之差较大Δe=0.61.其聚合机理和阴离子聚合原理差不多.因两个甲基基团的强推电子作用(即诱导效应)，使碳-碳之间π键的电子分布发生较大的偏移，导致原子的电荷分布不均匀，碳-碳π键断裂时只能发生异裂，最后只能发生阳离子聚合.图6也是由同样的方法得到的CH2=CHOCH3单体分子的几何构型和原子净电荷分布情况.可以发现其净电荷之差较大Δe=0.57.因它有甲氧基，而甲氧基具有很强的推电子作用(即诱导效应)，使碳-碳之间π键的电子分布发生较大的偏移，导致分子的电荷分布不均匀，则碳-碳π键之间只能发生异裂，从而只能发生阳离子聚合.从以上分析可看出，当原子净电荷之差较大时(Δe>0.35), 乙烯类单体聚合机理为阴或者阳离子聚合.

图3 CH2=CF2分子几何构型及净电荷分布 图4 CH2=CFCF3分子几何构型及净电荷分布Fig. 3 The geometrical configuration and the distribution of the atomic net charge of CH2=CF2 Fig. .4 The geometrical configuration and the distribution of the atomic net charge of CH2=CFCF3

图5 CH2=C(CH3)2分子的几何构型及净电荷分布 图6 CH2=CHOCH3分子的几何构型及净电荷分布Fig. .5 The geometrical configuration and the distribution of the atomic net charge of CH2=C(CH3)2 Fig. .6 The geometrical configuration and the distribution of the atomic net charge of CH2=CHOCH3

2.3 特殊结构单体乙烯基单体的几何构型及净电荷分布

选择特殊结构单体如CH2=CHF和C6H5CH=CH2进行分析.图7是由Gaussian03密度泛函理论(DFT)方法得到的CH2=CHF单体分子的几何构型和原子电荷分布情况.可以看到碳-碳原子之间的净电荷之差较大Δe=0.57，按规律应该发生离子聚合的，但是其聚合机理是自由基聚合.这可能与氟原子的半径较小(与氢原子半径接近)有关.如图8 是由同样的方法得到的C6H5CH=CH2单体分子的几何构型和原子电荷分布情况.从图中我们看到碳-碳原子之间的净电荷之差适中Δe=0.23，因净电荷之差可判断该分子可能发生自由基聚合或者离子聚合，但是其聚合机理是三种聚合机理都可以发生.这是因为苯环上面的大π电子与碳-碳π键上的π电子发生了π-π共轭作用，而使分子整体具有电子的流动性，从而导致三种聚合机理都可以发生.从这两个例子也说明，运用密度泛函理论来判断乙烯基类单体聚合机理时必须考虑特殊情况.

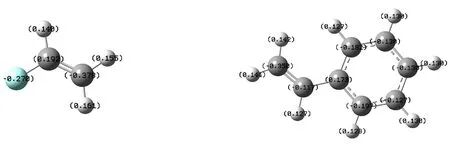
图7 CH2=CHF分子几何的构型及净电荷分布 图8 C6H5CH=CH2分子的几何构型及净电荷分布Fig. .7 The geometrical configuration and the distribution of the atomic net charge of CH2=CHF Fig. .8 The geometrical configuration and the distribution of the atomic net charge of C6H5CH=CH2

3 结论

运用密度泛函理论DFT-B3LYP方法，在6-31 d基组水平上，全优化计算了乙烯基类化合物分子的几何构型和原子净电荷分布情况.结论表明，当净电荷差较小(Δe<0.10)时,一般为自由基聚合;当净电荷差较大(Δe>0.35)时，一般为阴离子聚合或阳离子聚合;并分析了一些特例产生的原因，如因共轭作用使分子的电子具有流动性而同时具有三种聚合反应机理.最后所得结果基本与实际结果[6]吻合.该方法提出了一种新的对乙烯基类单体聚合机理的判断方法.

[1] 陈敏娥，甘雄，李茂莲.Keggin型多阴离子[XWl2O40]—(x =Si，Ge，P，As)电子性质的密度泛函理论研究[J].化学世界，2009(10): 597-600.

[2] 刘小村,季燕菊.C10H18N2O4Pt结构和性质的密度泛函理论研究[J].山东建筑大学学报,2009,24(5):429-433.

[3] 赵军宁,杨宗邃,马建中.乙烯基类化合物接枝改性淀粉的研究进展[J].中国皮革,2004,33(11):10-14.

[4] 周亚红,朱俊武,杨绪杰,等.正丁基锂引发甲基丙烯酸乙酯阴离子聚合的理论研究[J].南京理工大学学报，2007，31(3):380-384.

[5] Frisch M J,Trucks G W,Schlegel H B,et al.Gaussian 03[M].Pittsburgh PA:Gaussian Inc.,2003.

[6] 潘祖仁.高分子化学[M].4版.北京：化学工业出版社，2007:61-62.