卫星和飞船的跟踪测控研究

2011-01-18王玉梅

湖北民族大学学报(自然科学版) 2011年1期

关键词：测控飞船全程

王玉梅

(菏泽学院数学系,山东菏泽 274015)

1 问题的提出与分析

1.1 问题提出

卫星和飞船在国民经济和国防建设中有着重要的作用，对它们的发射和运行过程进行测控是航天系统的一个重要组成部分，理想的状况是对卫星和飞船(特别是载人飞船)进行全程跟踪测控.

测控设备只能观测到所在点切平面以上的空域，且在与地平面夹角3度的范围内测控效果不好，实际上每个测控站的测控范围只考虑与地平面夹角3度以上的空域.在一个卫星或飞船的发射与运行过程中，往往有多个测控站联合完成测控任务，如神州七号飞船发射和运行过程中测控站的分布如图1[1]所示.

利用模型分析卫星或飞船的测控情况，请分析问题：在所有测控站都与卫星或飞船的运行轨道共面的情况下至少应该建立多少个测控站才能对其进行全程跟踪测控？

1.2 问题的分析

本题主要是通过建立卫星全程测控模型，解决对卫星或飞船运行轨道的全程跟踪测控至少所需的测控站点个数问题.由题目所给信息分析得出，只要所建立的测控站点满足卫星或飞船在低轨道[2]的运行情况，它就必满足在中、高轨道的运行情况.

对于该问题，将地球及卫星或飞船的运行轨道理想化.由于低轨道的运行范围是在离地面200 km到400 km之间，在所有测控站都与卫星或飞船的运行轨道共面的情况下，依据所给的信息，分别计算出卫星或飞船在200 km与400 km所需设立的测控站点数，以此计算出在所有测控站点都与卫星或飞船的运行轨道共面的情况下至少应建立的测控站点数目.

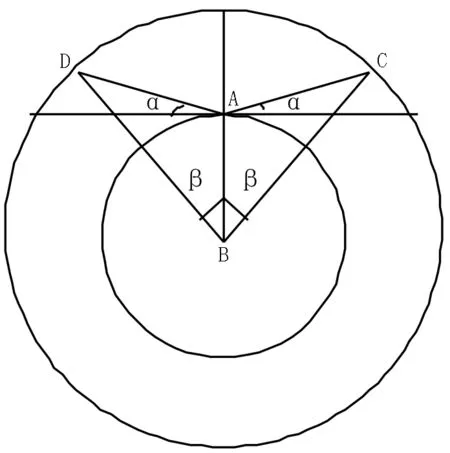
图2 测控站点与运行轨道平面图Fig.2 Monitoring the site plans with the orbit

2 模型的建立与求解

2.1 模型假设

1)发射地点的降水、地面风速小于8 m/s、水平能见度大于20 km；

2)发射前8 h至发射后1 h，场区30 km至40 km范围内无雷电活动；

3)发射所经过空域3 km至18 km高空最大风速小于70 m/s，此外发射前后9 h不能有雷电；

4)卫星或飞船的运行轨道以及地球都假设为理想的圆形；

5)卫星或飞船的运行轨道都是以地心为中心.

2.2 符号说明

R:地球半径(km)

H：卫星或飞船距地面的高度(km)

α：测控设备与地平面的夹角(α=3°)

2β：一个测控站观测卫星范围的弧长所对的圆心角

X:X=AC(如图2)

n:测控站的站点数

θ：卫星或飞船的运行轨道与地球赤道平面的固定夹角

r1：北纬22.5°处与赤道面平行的圆面的半径

n1：北纬22.5°处所需要的测控站点数目

n2：北纬45°处所需要的测控站点数目

n3：北纬67.5°处所需要的测控站点数目

n4：北级极点处所需要的测控站点数目

n0：北半球总共需要的测控站点数目

v1：卫星运行速度

v2：地球自转速度

d：测控站点所能测控范围的直径(图五CD长度)

t：使运行范围得到最大测控的时间

ω：在星下点轨迹[3]中两相邻测控站点所对应地心的圆心角

S1: 一个测控站点所能测出的卫星或飞船的运行轨道面积

2.3 模型建立

2.3.1 卫星低轨道在所有测控站都与卫星或飞船的运行轨道共面的情况下，只需考虑低轨道运行的情况，因为在卫星发射的过程中只要低轨道阶段在测控范围内，那么剩余的两个阶段自然会在测控范围之中，这是由于，高度越高被同一测控站测控到的范围越大[4].基于低轨道的运行范围在离地面200 km到400 km之间，根据题目所述：测控设备只能观测到所在点切平面以上且与地平面夹角3度以上的领域，依此建立卫星全程测控模型，以地心为圆心，以R+h为半径做与地球同心的一个圆,视为卫星低轨道运行的轨道,如图2.

那么会有:

cos(90°+α)=[R2+X2-(R+H)2]/2*R*X

(1)

cosβ=[R2+(R+H)2-X2]/2*R*(R+H)

(2)

n=360°/(2*β)

(3)

由式(1)、(2)和式(3)，并通过Matlab程序计算得到：

当R=6 400 km，H=200 km时：

n≈16

当R=6 400 km，H=400 km时：

n≈11