基于固碳效益的森林最优轮伐期的确定

王群超

(北京大学，北京，100871)

基于固碳效益的森林最优轮伐期的确定

王群超

(北京大学，北京，100871)

简述了国外基于固碳效益的最优轮伐期的研究。大量研究表明，当考虑人工林的固碳效益时，轮伐期长短会受影响，并会随碳价、贴现率变化而变化，并且这种变化通常很灵敏。通过总结国内关于森林固碳效益方面的研究，推导出固碳效益的一般模型，并将其引入到Faustmann最优轮伐期模型中，从而整理出基于固碳效益的最优轮伐期模型。

森林;固碳效益;最优轮伐期

我国有丰富的人工林资源，根据第七次全国森林资源清查结果，人工林保存面积达到6 168.84万hm2，人工林蓄积达19.61亿m3，人工林面积居世界首位。与此同时，我国的集体林权制度改革也已经成功开展，并取得了很大的成效。2006年7月，中共中央国务院发布了《关于全面推进集体林权制度改革的意见》，在坚持集体林地所有权不变的前提下，依法将林地承包经营权和林木所有权，以家庭承包的方式落实到农户，确立了农民作为林地承包经营权人的主体地位。随着林权的不断下放，林业市场也更加开放，那么如何获得人工林经营的净效益最大化成为林业经营者关注的核心问题。为此，经营者通常在经营管理的过程中需要解决两方面的问题:一是技术问题，比如调整林分种植结构、建立森林健康监测体系、改善土壤环境、防治病虫害等;一是经营策略问题，即如何根据市场条件调整林业经营方案，比如轮伐期的问题，一个最优的轮伐期可以有效降低林业投资的风险，提高经营者的回报率。

森林除了具有可观的经济价值，更具有巨大的环境价值，对于考虑环境价值的天然林开发来说，最优的轮伐期可以使得森林对社会的效益达到最佳。在当今全球气候变暖的背景下，人们更加关注二氧化碳的减排问题，增加森林碳汇已成为减碳的一个重要举措，关于森林固碳效益的研究也越来越受关注。在此背景下，文中探讨了基于固碳效益的森林最优轮伐期的确定。

1 研究进展

1.1 国外研究现状

国外对基于固碳效益的轮伐期确定问题有很多研究，比较突出的是对桉树的研究，而且对固碳量的核算已经不限于静态的研究，更多的是动态研究。多数研究发现，考虑固碳效益时，轮伐期会有一定的延长，对于不同的树种和立地条件，轮伐期的变化会有很大的差别，而且轮伐期的长短会受碳价、贴现率的影响，并且这种影响通常是非常灵敏的。

Luis D B等人[1]对比了巴西和西班牙的基于固碳效益的桉树最优轮伐期问题，发现当考虑固碳效益时，最优轮伐期和土地期望价值都会发生变化，并且轮伐期会非常敏感地随着某些参数(碳价、贴现率等)的变化而变化。Mejia E T等人[2]以墨西哥瓦哈卡州为例进行了研究，发现考虑固碳效益时，净现值和最优轮伐期都会受不同立地条件和林业产物的影响。在两种物种和生境指数下，不考虑固碳效益时，立木的轮伐期分别为83～108个月和108～163个月;当考虑固碳效益时，轮伐期的长度分别延伸了12～20个月和17～30个月。轮伐期延长后，碳市场净现值和效益费用比也相应地增加。

许多研究都表明，当考虑到固碳效益时，对于均龄森林来说都会产生一个较长的轮伐期，Sohngen B等人[3]以美国西部和南部的软木森林为例，探究了扩大的轮伐期内潜在的固碳成本和固碳量。在一定碳价下，把碳的价值带入最优轮伐期模型，计算了324种软木材所增加的成本。结果显示在12个州，1 500万t二氧化碳可以以7美元/t的成本被固定，对于高达55～209美元/t的碳价来说是十分合算的。另外，研究发现林木价格对于固碳的边际成本有重要影响，其次为立地质量。在55美元/t的碳价下，将有100 hm2的软木森林被保留。

John G等人[4]研究了美国新罕布什尔州人工林的净固碳量及林木资源开采情况，发现在没有政策鼓励增强森林固碳效应时，经营者倾向于选择较短的轮伐期而进行全部砍伐。基于一个保守的假定，即考虑固碳的社会效益的话，对于不同的森林来说，轮伐期可以延长16～133 a;如果决策者推崇一个成本效益策略，使大气中碳的量稳定在工业化以前的两倍的话，那么最优轮伐期可达180～347 a。

Chladna Z[5]研究了随机条件下碳交易的最优轮伐期的确定，通过建立一个选择模型来表达林木价格和碳价的不确定性，进一步在考虑或不考虑固碳效益两种情形下讨论，发现最优轮伐期随着价格类型、碳收益的定价方式和贴现率的不同而变化。

1.2 国内研究现状

目前，国内有许多关于固碳效益的研究报道，但尚未见基于固碳效益的轮伐期问题的研究报道。这些研究大多是通过估算生物量或森林蓄积量，然后采用固定二氧化碳成本法、碳税法、造林成本法、支付意愿法等方法确定碳价，计算某个林区的固碳效益。宋离东等[6]通过引入“市场逼近系数”，构造出森林固碳效益的经济结构模型，计算了福建省森林的固碳效益。林家淮等[7]根据光合作用和呼吸作用的反应方程式，以及东江源区活立木总蓄积量、立木蓄积年平均生长率，计算出东江源区森林的年固碳量，采用平均造林成本法计算出该区的固碳效益。张治军等[8]对比了广西主要人工林类型在一个轮伐期内固碳成本的变化并分析了其敏感性，同时分析了贴现率对固碳成本的影响。研究结果表明，主要人工林固碳成本的净现值随树龄增加而降低，用不同贴现率计算各树种轮伐期末的固碳成本现值，发现相差较大。吴霞[9]也利用植物光合作用方程式，并根据森林的蓄积量计算出固碳量，结合碳税率或造林成本，得到小陇山林区森林固碳效益。刘璨[10]建立了森林固碳量与林地、森林资源及其它依赖森林资源生存的资源的固碳量的回归方程，计算出固碳总量，并用支付意愿法确定碳价格，从而算出森林的固碳效益。姜东涛[11]总结了3种计算制氧固碳效益的方法，采用造林成本法、干物质生长量平均售价、森林培育成本价，分别计算了黑龙江林区的固碳效益，并利用干物质生长量平均售价方法计算出黑龙江省森工林区现有森林的总固碳效益。

2 在考虑固碳效益前提下的最优轮伐期的表达

2.1 固碳效益的表达

根据森林蓄积量和碳税法、造林成本法等的计算方法，推导出了森林固碳效益(F(t))的表达式:

式中:M(t)为森林固碳量;Q(t)为森林蓄积量;a为系数(a＞0);p为碳价。

根据大量的理论和实证研究，某一时刻的固碳量和森林的蓄积量是成正线性相关关系的(此处未考虑土壤的固碳效应)。碳价(p)可根据碳税法、造林成本法、支付意愿法等方法确定。

2.2 单个轮伐期的表达

根据Faustmann的单个轮伐期模型[12]62，对于单个轮伐期有以下假定:(1)林场由个人或公司经营，市场是自由竞争的;(2)通过签订合同，林场经营者面临选择一个可以持续经营的轮伐期问题，以求得净现值的最大化;(3)林木是在同一个时期种植的，所有林木处于同一个成长期;(4)森林可以砍伐获得收益，即木材价值，同时森林在未砍伐时具有固碳效益。

以t=0为起点，所有的林木都是在此刻进行种植，令Q=Q(t)，Q(t)代表t时刻森林的林木蓄积量。一般来说，林木的蓄积量会随着时间的推移逐渐增大，最终会达到一个最大值。比较常见的两类表达形式为:

在Faustmann的单个轮伐期模型中，假定采伐时单位木材价格p1是不变的，并且一个轮伐期的时间长度t=T，砍伐后不再种植。那么，轮伐期末的木材价值可以表示为:

在森林的生长阶段，会有一个持续的固碳效益，根据(1)式，可以表达为:

为了简便，此处未考虑森林的其他服务价值及森林的维护成本，但考虑森林在刚开始种植时有一个固定成本(C0)。根据Snyder等对Richard Hartman模型的进一步优化，而提出的森林多重利用价值时最优轮伐期的模型，可以给出单个轮伐期内基于森林固碳效益的单个轮伐期净现值:

式中:e-rt是贴现因子(将未来的经济收益贴现到现在);r是社会贴现率;T是轮伐期;G(t)是木材的商品价值;F(t)是森林的固碳效益。

将(4)、(5)两式带入净现值的计算公式((6)式)，得:

使净现值最大化，令V′1=0，可求出最优轮伐期，即:

整理后得到关于轮伐期的隐函数:

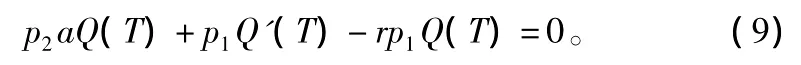
对于不同的森林，应用不同的森林蓄积量函数，就可以得出最优轮伐期的T值。

2.3 多个轮伐期的表达

根据 Faustmann 的多个轮伐期模型[12]63-65，对于多个轮伐期有以下假定:(1)市场是自由竞争的;(2)林场经营者可以永远经营，期望实现净现值的最大化;(3)林木是在同一个时期种植的，所有林木处于同一个成长期;(4)森林砍伐后获得木材价值，同时森林在未砍伐时具有固碳效益。

根据Faustmann的轮伐期模型，在所有的轮伐期末可以获得的木材收益都是相同的，木材收益可以表示为[p1Q(T)-c]，其中c是种植林木的成本，经过贴现后的木材价值的净现值为:

整理后得:

同理，对于固碳效益有:

考虑固碳效益的多个轮伐期净现值为:

使净现值最大化，令V′2=0，整理后得:

对于不同的森林，将蓄积量函数带入上式，就可以求得多个轮伐期的T值。

3 结束语

轮伐期是林业经营中经营者的重要决策依据，它决定了林业经营投资风险的大小。目前来看，在人工林的经营过程中，由于碳市场的不完备和人们缺乏认识等原因，经营者基本不会考虑森林的固碳效益;但在较大型林区，已有很多关于森林固碳效益的研究，人们也逐渐认识到森林固碳的巨大收益。

只考虑木材的立木价值，经营者倾向于较早地砍伐林木，使得轮伐期变短，如果考虑到森林的固碳效益，轮伐期会延长，人们倾向于较晚地砍伐林木，这样对增加我国森林的固碳量是大有益处的。另外，森林不仅有固碳效益，还有涵养水源、防风固沙、维持生物多样性等众多生态服务功能，很多研究表明其环境价值已远远超过了本身的立木价值。可见，对考虑森林环境价值的经营策略进行研究具有重要意义。此外，对森林环境价值的认识和宣传也是一项长期而又艰巨的任务。

[1] Luis D B，Luiz C E R.Optimal rotations on Eucalyptus plantations including carbon sequestration-A comparison of results in Brazil and Spain[J].Forest Ecology and Management，2006，229(1/3):247-258.

[2] Mejia E T，Guillen M D G，Posadas H M D，et al.Optimal timber rotation lengths in eucalyptus plantations including revenues from carbon capture in Oaxaca，Mexico[J].Revista Fitotecnia Mexicana，2008，31(2):173-182.

[3] Sohngen B，Brown S.Extending timber rotations carbon and cost implications[J].Climate Policy，2008，8(5):435-451.

[4] John G，Richard B H.Carbon sequestration and the optimal management of New Hampshire timber stands[J].Ecological Economics，2007，62(3/4):441-450.

[5] Chladna Z.Determination of optimal rotation period under stochastic wood and carbon prices[J].Forest Policy and Economics，2007，9(8):1031-1045.

[6] 宋离东，张江山.福建省森林固定CO2价值评估[J].云南环境科学，2005，24(3):24-26.

[7] 林家淮，欧书丹，刘良源.东江源区森林涵养水源、固碳制氧价值估算[J].江西科学，2009，27(2):247-250.

[8] 张治军，张小全，朱建华，等.广西主要人工林类型固碳成本核算[J].林业科学，2010，46(3):16-22.

[9] 吴霞.小陇山林区森林固碳效益的研究[J].西北林学院学报，2008，23(5):164-167.

[10] 刘璨.森林固碳与释氧的经济核算[J].南京林业大学学报:自然科学版，2003，27(5):25-29.

[11] 姜东涛.森林制氧固碳功能与效益计算的探讨[J].华东森林经理，2005，19(2):19-21.

[12] Jon M C.Resource Economics[M].New York:Cambridge University Press，1999.

Determination of Optimal Rotation Age for Forest Stands Based on Carbon Sequestration Benefits

/Wang Qunchao(College of Environmental Sciences and Engineering，Peking University，Beijing 100871，P.R.China)//Journal of Northeast Forestry University.-2011，39(6).-98～100

Forests;Carbon sequestration benefits;Optimal rotation age

S753

王群超，男，1987年7月生，北京大学环境科学与工程学院，硕士研究生。

2010年12月4日。

责任编辑:李金荣。

The paper deals with the studies on optimal rotation age for forest stands based on carbon sequestration benefits in foreign countries.Many researches show that the consideration of carbon sequestration benefits will have an effect on rotation age.The rotation age is quite sensitive to carbon price and discount rate.A general model for calculation of forest carbon sequestration benefits was deduced by analysis of the domestic researches on forest carbon sequestration benefits.Then，the model was introduced into the Faustmann model for the determination of optimal rotation age;thereby，optimal rotation models based on forest carbon sequestration benefits were created.