动态测量不确定度贝叶斯评定的改进方法研究
2011-01-17李世平翟兆松文超斌
宋 兵,李世平,翟兆松,文超斌
(第二炮兵工程学院,陕西 西安 710025)
动态测量不确定度贝叶斯评定的改进方法研究
宋 兵,李世平,翟兆松,文超斌
(第二炮兵工程学院,陕西 西安 710025)
动态测量不确定度的评定一直是比较复杂的问题,到目前为止,国内外有许多学者对这一问题进行了探索与研究,给出了一些评定的方法,但这些方法都存在自身的缺点与不足,还不能给出十分精确的评定结果。因此,通过对现有基于贝叶斯理论的动态测量不确定度评定方法进行分析,用最大熵原理改进其先验分布的选择与计算方法,从而有效提高计算后验分布的精度,最终提高不确定度的计算准确度。
最大熵原理;蒙特卡洛方法;灰自助方法;贝叶斯方法;动态测量不确定度
1 引 言
文献[1]中提出了基于贝叶斯理论的动态测量不确定度评定方法,具有能够充分利用先验信息来增加评定的信息量的优点,同时采用贝叶斯动态线性模型对不确定度进行计算,体现动态测量系统的特性,是一个计算动态测量不确定度的有效方法。但该方法也存在不足,先验分布的选择及计算方法,由于后验分布的精度直接受到先验分布精度的影响,因此必须准确计算先验分布。
文献[1]中先验分布的选取及计算方法为:(1)主观概率法,此方法主观因素较多,不能精确客观地体现先验信息的真实概率分布;(2)先验信息确定法,虽然主观因素较少,但仍然不是计算先验分布的最佳方法。
2 最大熵原理及样本分布的计算
2.1 最大熵原理
熵的概念最先在1864年由克劳修斯提出,1948年美国电器工程师香农(Shannon C.E)在《通信的数学理论》中,把“熵”用来表示一个随机事件的“不确定性”或信息量的量度。最大熵原理是在1957年由Jaynes E.T.提出的,其主要思想是在只掌握关于未知分布的部分样本时,应该选取符合这些样本但熵值最大的概率分布。实际上熵表征的是一个随机变量的不确定性,熵最大时,说明随机变量的随机性最好。最大熵原理实质是:在已知部分样本的前提下,对未知分布最合理的推断是基于已知样本的最不确定或最随机的即熵最大的推断,任何其他的推断都意味着无形中增加了未知的约束和假设,而这些未知的约束和假设是无法获知的。因此运用最大熵原理得到的样本的概率分布要明显优于其他方法。
一个离散随机变量X,其概率分布函数为p(x),则X的不确定性用熵H(x)表示:


3 先验分布确定方法的改进
通过研究文献[1]中先验分布计算方法的不足,提出了改进方法,将其分为无信息先验分布确定法和有信息先验分布确定法。
3.1 无信息先验分布确定法
在没有先验信息可利用的情况下,对先验分布的计算一直是一个难点,该文采用的方法是:首先由测量系统获得少量实验数据,通过蒙特卡洛方法与灰自助方法进行样本扩充,其次通过最大熵原理基于扩充后的新样本计算先验分布。此方法在无任何先验信息的情况下,通过现场测得的少量测量数据代替先验信息,较大程度上弥补无先验信息的不足。
3.2 有先验信息确定法
在有先验信息的情况下,采用基于最大熵原理的先验分布计算法,此方法是最随机、主观假设最少的先验分布确定法。先验分布计算流程图见图1。

图1 先验分布计算流程图
4 后验分布及动态不确定度的计算
若θ为连续的随机变量,涉及θ的样本信息记为X,则后验分布表示为:

式中:h(θ|x)——后验分布;
p(θ)——先验分布;
L(θ|x)——似然函数。
通过将计算得到的先验分布代入式(11)即可获得后验分布。
按照该文先验分布的确定方法及文献[1]所述动态测量不确定度计算方法计算动态测量不确定度,流程图如图2所示。
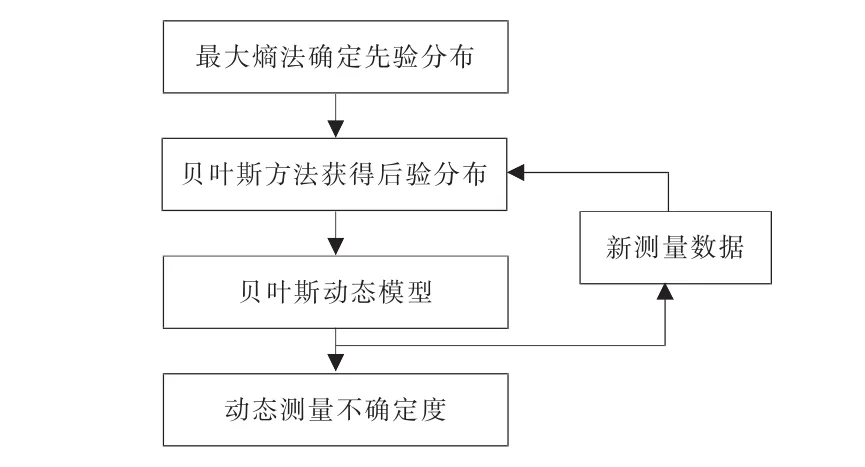
图2 动态测量不确定度评定流程
5 实例分析
用工业控制计算机通过GPIB总线控制Agilent33250任意函数发生器产生如式(13)所述的信号:

通过Agilent34401六位半数表进行数据采集,共采样5组,每组10个采样点。数据采集结果如表1所示,数据误差分析结果如表2所示。
应用蒙特卡洛方法、灰自助方法进行样本扩充后,基于最大熵原理计算先验分布与基于文献[1]方法计算先验分布得到的动态测量不确定度如表3所示。
表3给出由贝叶斯方法及最大熵改进方法计算得到的动态测量不确定度、误差及改进方法对于贝叶斯方法的相对偏差。通过分析,由最大熵方法确定先验分布计算得到的动态测量不确定度的精度要高于文献[1]中贝叶斯方法的精度,说明所做的改进是有效的,在很大程度上弥补了文献[1]中求先验分布方法精度不高的不足,从而有效地提高了计算动态测量不确定度的准确度。
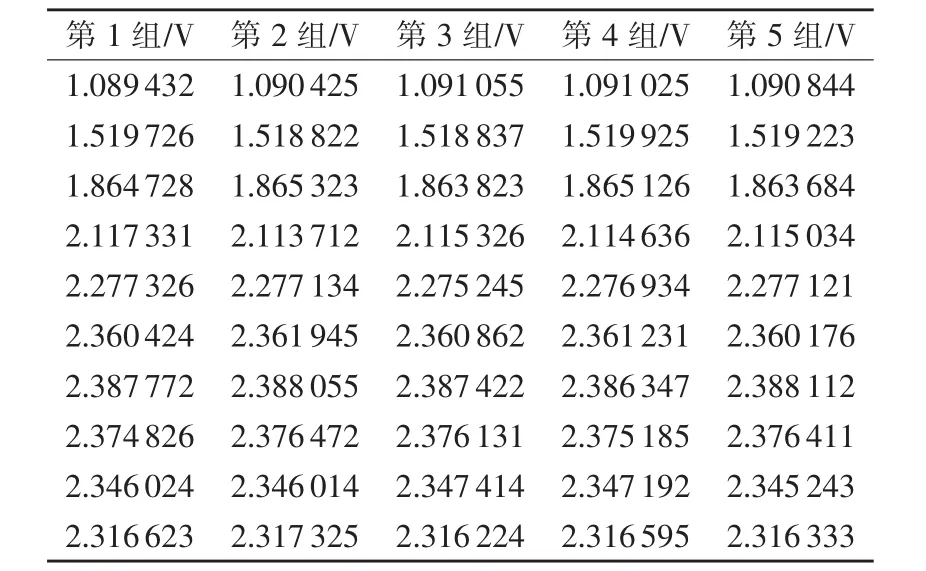
表1 试验数据
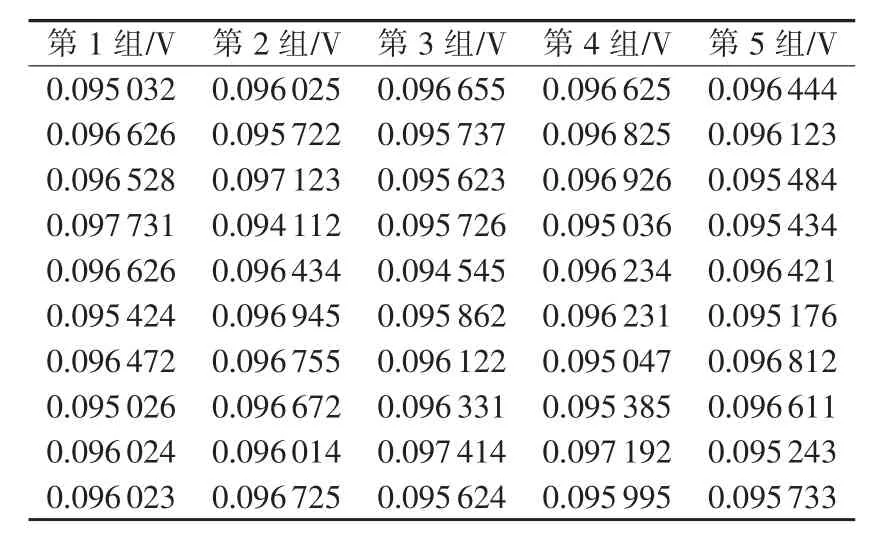
表2 试验数据误差
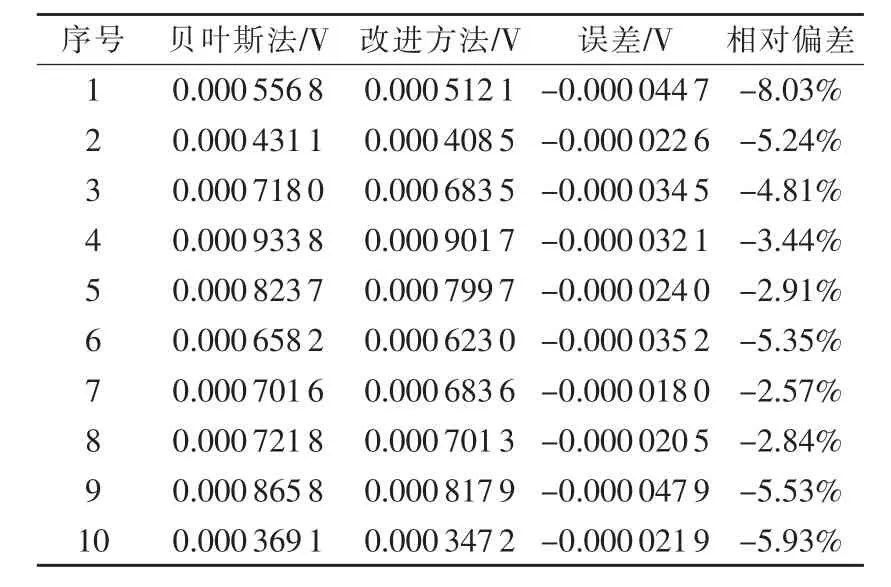
表3 动态测量不确定度结果1)
6 结束语
基于最大熵原理及蒙特卡洛、灰自助方法对文献[1]贝叶斯先验分布的确定方法进行了改进,解决了无先验信息情况下的先验分布确定方法,通过最大熵原理计算先验分布,提高了动态测量不确定度的评定准确度。
[1]高玉英.基于贝叶斯理论的动态不确定度评定方法研究[D].合肥:合肥工业大学,2007.
[2]程真英.动态测量误差的贝叶斯建模预报及其不确定度研究[D].合肥:合肥工业大学,2004.
[3]薄晓静.基于贝叶斯理论的不确定度评定方法[D].合肥:合肥工业大学,2005.
[4]朱坚民,郭冰著,王中宇,等.基于最大熵方法的测量结果估计及测量不确定度评定[J].电测与仪表,2005,42(476):5-8.
[5]黄建新,边亚琴.基于蒙特卡罗仿真的雷达装备重要度评价[J].兵工自动化,2009,28(9):26-28.
[6]李 喆,丁振良,袁 峰.飞行器姿态参数的光学测量方法及其精度的蒙特卡罗模拟[J].吉林大学学报,2009,39(5):1401-1406.
[7]杨 明,张可能,刘宇飞.基于Matlab的均质土坡稳定可靠度的蒙特卡罗模拟[J].地质与勘探,2009,45(1):89-94.
[8]李 响,贾明涛,王李管,等.基于蒙特卡罗随机模拟的矿岩崩落块度预测研究[J].岩土力学,2009,30(4):1186-1190.
[9]余秀美,童 玲,胡学海.基于Matlab最大熵分布的最优解[J].电子测量与仪器学报,2004(增刊):98-103.
[10]孙永厚,周洪彪,黄美发.基于最大熵的测量不确定度的贝叶斯评估方法[J].统计与决策,2008,12(264):143-145.
Im proved method of dynam ic measurement uncertainty evaluation of Bays method
SONG Bing,LI Shi-ping,ZHAI Zhao-song,WEN Chao-bin
(Second Artillery Engineering College,Xi’an 710025,China)
Assessment of dynamic measurement uncertainty is a complicated problem and has
much attention.Many researchers have studied this problem and provided assessing methods.However,these methods still have their limitations and cannot provide accurate result.In this paper,a new method based on Bays theories was presented to for the calculation of measurement uncertainty.By analyzing existing methods and using Maximum Entropy Method(MEM) to calculate former distribution,the accuracy of behind distribution can be improved,thus the accuracy of measurement uncertainty can be improved.
Maximum Entropy method; Monte Carlo method; Gray Bootstrap; Bays method;dynamic measurement uncertainty
O212.8;TM930.115
A
1674-5124(2011)01-0035-03
2010-03-23;
2010-06-15
宋 兵(1985-),男,辽宁丹东市人,硕士研究生,专业方向为检测技术与自动化装置、动态测量理论。
