基于螺纹基本牙型和参数定义的最佳测针直径

宫美望，王召孟，刘文君

（1.青岛市计量测试所，山东 青岛 266071；2.青岛市水利勘测设计研究院，山东 青岛 266071）

基于螺纹基本牙型和参数定义的最佳测针直径

宫美望1，王召孟1，刘文君2

（1.青岛市计量测试所，山东 青岛 266071；2.青岛市水利勘测设计研究院，山东 青岛 266071）

针对不同种类螺纹中径的测针测量法，论证最佳测针直径的计算方法和前提条件。根据具体被测螺纹的设计原理和测量方法，重点讨论了其基本牙型和参数定义方法对最佳测针直径的影响。通过几何分析和理论推导，明确了相应的螺纹中径计算公式和最佳测针直径的确定方法。准确的最佳测针直径可以减小螺纹中径的测量误差，尤其是在理论上可以避免牙型角偏差引入的螺纹中径测量误差。

螺纹中径；最佳测针直径；基本牙型；参数定义；原始三角形高度

1 引 言

一般情况下，螺纹直径参数在垂直于螺纹轴线的方向定义，螺距在轴线方向定义，原始三角形高度和牙型高度均定义在垂直于轴线的方向上。但是对于我国生产的气瓶专用螺纹，其螺距在圆锥体母线方向定义，且原始三角形高度和牙型高度均定义在垂直于圆锥体母线的方向上，可直径参数定义在垂直于轴线的方向上（位于基面）。此时采用“测针法”测量圆锥外螺纹中径时，最佳测针直径的计算应该特别注意。

另外，NPT螺纹的最佳测针直径计算方法，其与米制普通圆柱外螺纹和前述我国生产的气瓶专用螺纹不同，以下将有详细分析，且给出了文献[1]、文献[2]、文献[3]和文献[4]中所采用最佳测针计算公式的不足之处。

2 米制普通圆柱外螺纹（M）

米制普通圆柱外螺纹（M）的牙型角为60°，基本牙型和参数定义如图1所示，主要用于紧固连接，应用广泛。最佳测针与牙侧的两接触点都位于中径线上，使用测针法测量螺纹中径时，在不考虑修正值的情况下，则中径d2的计算公式：

依据图1的几何关系可知BC的计算方法：

图1 普通圆柱外螺纹的基本牙型

式中：M——“测针法”测量时的读数值；

H——螺纹原始三角形高度；

d——最佳测针直径；

P——螺距；

依据式（3），因为 α=60°，则米制普通圆柱外螺纹原始三角形高度H=0.866025P。

2.1 米制普通圆柱外螺纹的最佳测针直径d的计算方法

对于米制普通圆柱外螺纹，依据“测针法”的测量原理和基本牙型及参数定义，在不考虑螺旋升角的影响时，则最佳测针直径d的计算公式为：

对于米制普通圆柱外螺纹，最佳测针直径采用式（5）进行计算。

另外，在使用“测针法”测量外螺纹中径时。最佳测针外圆外侧与齿顶之间的距离S为原始三角形高度H的。因此，在不得不使用非最佳测针时，则测针直径选择应保证测针与牙侧的接触点偏离中径位置的距离小于牙侧长度（角边长），以防止测量时发生干涉现象。关于这一点国家计量检定规程JJG 888-1995《圆柱螺纹量规》中第3页有相关规定。

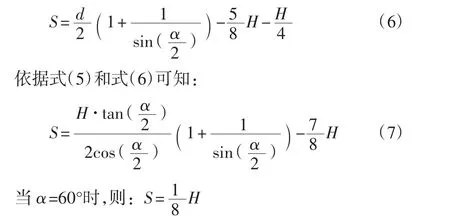
3 米制梯形螺纹（Tr）

米制梯形螺纹（Tr）的牙型角为30°，主要用于传动，也可用于紧固连接。

米制梯形螺纹的牙型角平分线垂直于轴线，螺距定义在轴线方向，锥度为零，螺纹基本牙型如图2所示。其原始三角形高度H的值可以采用式（3）计算，α=30°时，则 H=1.866025P，且规定 H1=0.5P。

图2 梯形外螺纹的基本牙型

3.1 米制梯形螺纹的最佳测针直径d的计算方法

对于米制梯形外螺纹，在不考虑螺旋升角的影响时，最佳测针直径也可以采用式（5）进行计算，因为其使用最佳测针测量中径时，理论上测针与牙侧的两接触点位于中径线上，且螺距定义在轴线方向。

另外，由于梯形螺纹基本牙型的特点，最佳测针外圆外侧与齿顶之间的距离S大约为原始三角形高度H的。因此，在不得不使用非最佳测针时，则测针直径应选择略大于理论最佳测针直径，以防止测量时发生干涉现象。关于这一点国家计量检定规程JJG 888-1995《圆柱螺纹量规》中第4页也有提及。

4 NPT密封圆锥外螺纹

NPT螺纹的基本牙型如图3所示，圆锥螺纹的牙型角平分线垂直于圆锥体轴线，且螺距P定义在轴线方向，锥度为1∶16，原始三角形高度H和牙型高度h均定义在垂直于圆锥体轴线的方向上。

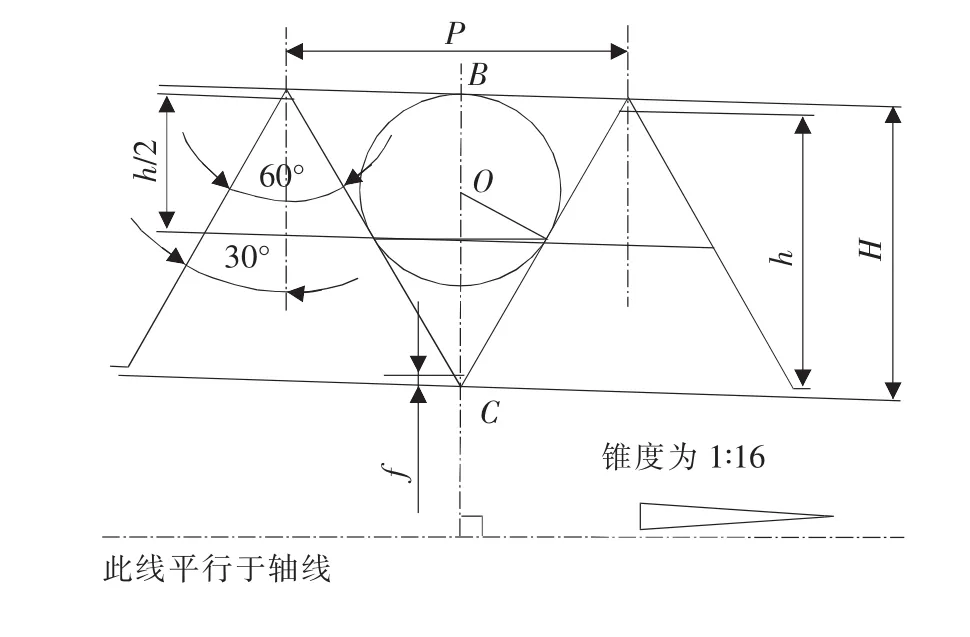
图3 NPT密封圆锥外螺纹的基本牙型

NPT螺纹基本牙型的原始三角形高度H：

4.1 NPT密封圆锥外螺纹的最佳测针直径d的计算方法

NPT螺纹使用“测针法”测量中径时，其最佳测针与螺纹牙槽侧面的两个接触点不可能位于中径线上，只能是这两个接触点的连线的中点位于中径线上，且此连线与中径线的夹角为圆锥半角。依据图3的基本牙型的几何关系和参数定义方法，结合式（4）和式（10），在不考虑螺旋升角的影响时，则最佳测针直径d的计算公式为：

式（10）和式（11）中：

H——NPT螺纹原始三角形高度；

d——最佳测针直径；

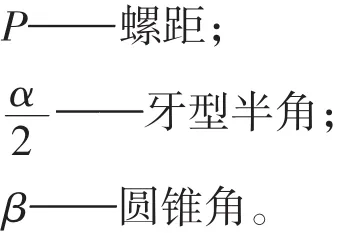
需要说明的是，文献[1]、文献[2]、文献[3]和文献[4]中都给出了密封圆锥外螺纹中径测量时最佳测针的计算公式。其公式形式一致，如式（12）所示。

其中φ在文献[2]和文献[3]中均认为是圆锥角，而按照文献[1]中的约定则认为是“测量实际中径处的螺旋升角”。

可在式（12）中无论φ是圆锥角还是“测量实际中径处的螺旋升角”，式（12）的正确性都值得商榷。

首先，假定式（12）中φ是圆锥角。在不考虑螺旋升角的影响时，在该圆锥螺纹的牙型角平分线垂直于圆锥体轴线且螺距定义在轴线方向时，最佳测针的计算公式应该采用式（11）。

然后，假定式（12）中φ是“测量实际中径处的螺旋升角”。一般在理想状态下，对于一般圆柱普通外螺纹其最佳测针与螺纹牙侧的两个接触点应该在中径线上，但是对于NPT密封圆锥外螺纹仅可保证其最佳测针与螺纹牙侧两个接触点的连线的中点位于中径线上。螺旋升角对测针和牙侧接触点（或接触点的连线的中点）的影响，是导致最佳测针位置的上移（或远离轴线外移），此时最佳测针直径应适当减小，以确保测针与牙侧接触点回落到理想位置。所以在考虑螺旋升角对最佳测针直径的影响时，应该是采用略小于最佳测针直径的理论计算值。

显而易见，从理论上分析，式（12）很难是一个正确的最佳测针直径计算公式。虽然螺旋升角较小时，其影响可以忽略不计。但是理论上的深入探讨，可使大家对螺纹基本牙型及螺纹参数几何意义的理解更加明了，明确了使用中径计算公式和最佳测针计算公式的前提条件是被测螺纹的基本牙型和参数定义方法，对其选用方法更准确更清楚。

5 气瓶专用外螺纹

图4 国标气瓶专用圆锥外螺纹的基本牙型

国标气瓶专用螺纹的基本牙型如图4所示，牙型角α=55°，锥度为3∶25，圆锥螺纹的牙型角平分线垂直于圆锥体的母线，且螺距P定义在锥体母线方向上，原始三角形高度H和牙型高度h均定义在垂直于圆锥体母线的方向上。

但是，国标气瓶专用螺纹的直径参数定义在垂直于轴线方向上（基面）。依据图4的基本牙型的几何关系和参数定义，原始三角形高度可以按照式（3）进行计算，即H=0.960491P。

5.1 国标气瓶专用圆锥外螺纹的最佳测针直径d的计算方法

虽然国标气瓶专用圆锥外螺纹与NPT螺纹均是圆锥外螺纹，但是不能采用式（11）来计算最佳测针直径，这是因为两者螺纹的基本牙型和参数定义不同。国标气瓶专用圆锥外螺纹使用最佳测针时，测针与牙侧的两个接触点均位于中径线上，这一点与NPT螺纹不同，另外螺距参数定义的方向也不相同。

结合图4的基本牙型的几何关系和参数定义，在不考虑螺旋升角的影响时，最佳测针直径可以采用式（5）来计算。

需要说明的是，以上最佳测针的计算是以我国生产的气瓶专用螺纹（例如，螺纹代号为PZ39、PZ27.8、PZ19.2）为例，且依据 GB/T 8335-1998《气瓶专用螺纹》和GB/T 8336-1998《气瓶专用螺纹量规》的螺纹基本牙型和参数定义来进行计算。

对于不同国家生产的气瓶专用螺纹，其依据的相应国家标准不同，则其基本牙型、参数定义也不同。具体而言，气瓶专用螺纹的规格、螺距、锥度、牙型角、牙型角平分线垂直于圆锥体母线或轴线的选择、基面距、螺纹中径加工精度、螺纹长度等也不是完全相同。所以最佳测针的计算方法和公式也有区别，必须依据被检气瓶螺纹的具体基本牙型和参数定义方法，具体问题具体对待。

6 总 结

前述4种螺纹类别的基本牙型和参数定义均不同，但是也有共同的特点：（1）螺纹的直径参数均在垂直于轴线方向定义。（2）螺距不一定在螺纹轴线方向定义，但是一定在垂直于牙型角平分线的方向定义。

（3）原始三角形高度和螺纹牙高参数不一定在垂直于轴线方向定义，但是一定在平行于牙型角平分线的方向定义。

正是基于以上特点，才使得螺纹本来复杂的空间曲面体变得相对简单，有规律可循。

6.1 关于最佳测针直径的通用计算方法

在（1）、（2）、（3）条件下，在采用“测针法”测量外螺纹中径且不考虑螺旋升角的影响时，最佳测针直径的计算均可采用通用式（4）计算，依据不同种类螺纹的原始三角形高度H和牙型半角可以计算出最佳测针直径。

6.2 关于螺纹中径的通用计算方法

（1）在采用“测针法”测量外螺纹中径时，不同种类螺纹的中径测量计算，无论是圆柱螺纹还是圆锥螺纹，在牙型角平分线垂直于轴线时，均可采用通用式（1）计算中径。

以NPT螺纹为例：

设图5中实际测量截面上的F点位于圆锥螺纹的基面偏小端一侧，且F点与NPT螺纹基面的距离为L，此种情况一般针对NPT螺纹塞规，由于结构原因很难直接在基面上测量NPT螺纹塞规的中径。NPT螺纹塞规一般为通规和止规一体，因此需要切出基面（一般标识为“0”）和通止规（一般标识为“下”和“上”）3个位置。

图5 NPT螺纹中径的测量

理想状态是直接在基面上测量中径，此时L=0，此种情况一般针对NPT螺纹工件，NPT外螺纹工件没有结构上的障碍。

假设NPT螺纹锥度为K，NPT螺纹基面中径d2的计算公式，可以依据式（1）、式（2）、式（10）则有：

式中：MV——虚拟M值，其测量方法比较简单，可参阅相关书籍。

（2）对于圆锥外螺纹，在牙型角平分线垂直于圆锥体母线时，由于螺纹中径定义在垂直于轴线的方向，其中径计算公式需要考虑圆锥半角的影响。只需要将图6中的OF投影到垂直于轴线的方向，本质上与中径通用计算式（1）相同。

以国标气瓶专用圆锥外螺纹为例：

图6 国标气瓶专用圆锥外螺纹中径的测量

设图6中实际测量截面上的F点位于圆锥螺纹的基面偏小端一侧，且F点与被测螺纹基面的距离为L，理想状态是直接在基面上测量中径，此时L=0。假设被测螺纹锥度为K，被测螺纹基面中径d2的计算公式：

7 结束语

由此可见，必须真正了解被测螺纹的基本牙型的几何意义和外螺纹参数定义方法，熟悉其结构特点，灵活运用式（1）和式（4），才能求出最佳测针和外螺纹中径的计算方法。

[1]费业泰.新编螺纹测量手册[M].合肥：安徽科学技术出版社，1988.

[2]JJG（石油）01-1996，石油钻具接头螺纹工作量规[S].北京：中国计量出版社，1996.

[3]王军培.NPT锥螺纹中径的一种测试方法及其测量不确定度评定[J].中国计量，2009（7）：93-95.

[4]徐孝恩.螺纹检验与测量[M].北京：中国计量出版社，1984.

[5]刘远模.螺纹环规单一中径的测量[J].计量技术，2005（6）：17-20.

[6]张成悌.现行螺纹量规公差存在的问题与解决办法[J].中国测试技术，2005（1）：24-25，36.

[7]梁 平.普通螺蚊环规检定中存在的问题与解决方案[J].计量与测试技术，2008，35（9）：11，14.

[8]余志新，钱景行，孟宪新，等.螺纹量规检验手册[M].北京：中国计量出版社，1985.

[9]张成悌.关于三针法测量螺纹中径的测力压陷变形问题[J].实用测试技术，1994（3）：13-16.

[10]李 柱.互换性与测量技术基础[M].北京：中国计量出版社，1985.

[11]JJG 888-1995，圆柱螺纹量规[S].北京：中国计量出版社，1995.

Optimum diameter of three w ires based on screw threads-basic profile and parameter definitions

GONG Mei-wang1，WANG Zhao-meng1，LIU Wen-jun2
（1.Qingdao Institute of Measurement and Testing，Qingdao 266071，China；2.Qingdao Water Conservancy Survey Design Institute，Qingdao 266071，China）

Different type of screw thread measurement needs different method.In this paper，the calculation method and precondition of optimum diameter for screw thread measurement were demonstrated.According to the design principle and measurement method of screw thread，the influences of screw threads-basic profile and screw thread parameters definition to the calculation of optimum diameter of three wires were discussed.Through geometric analysis and theoretical derivation，the calculation method of the screw thread pitch diameter and optimum diameter of the three wires was further confirmed.Accurate optimum diameter can reduce the measurement error of screw thread pitch diameter，and it can theoretically avoid measurement error introduced by screw thread angle deviation.

screw thread pitch diameter；optimum diameter of three wires for screw thread measuring；screw threads-basic profile；definition of screw thread parameter；fundamental triangle height

TG85；TM930.12

A

1674-5124（2011）01-0013-05

2010-01-25；

2010-03-10

宫美望（1965-），男，陕西户县人，高级工程师，主要从事精密测试技术研究。