基于季节调整模型的我国铁路客运量波动分析

桂文林，韩兆洲

（1.惠州学院 数学系，广东 惠州 516007；2.暨南大学 统计系，广东 广州 510632）

基于季节调整模型的我国铁路客运量波动分析

桂文林1，韩兆洲2

（1.惠州学院 数学系，广东 惠州 516007；2.暨南大学 统计系，广东 广州 510632）

在研究 TRAMO/SEATS季节调整模型计算方法的基础上，基于我国铁路 2002年1月—2010年 2 月的客运量月度数据，应用Demetra软件，通过季节调整模型参数设置、模型的估计和检验，得到 2010 年 3月—2012 年 2 月的铁路客运量预测值，并对预测结果进行趋势性和季节性分析。研究结果表明，Tramo/Seats 季节调整模型的预测精度较高。

铁路；TRAMO/SEATS模型；季节调整；客运量

由于受诸多主客观因素影响，铁路客运量表现出趋势、季节和随机性的复杂波动特征。季节调整模型能够很好地将时间序列进行分解，并将季节因素从原序列中剔除后找到变动趋势特征。因此，通过 TRAMO/SEATS 季节调整模型将我国铁路客运量月度数据时间序列进行分解，并用 Demetra 软件求解，在此基础上分析铁路客运量的季节和趋势特征，进行科学预测。

1 TRAMO/SEATS季节调整模型

美国经济学家于 1919 年首先提出季节调整问题，1931 年 Macauley 提出了移动平均比率法，成为季节调整方法的基础。SEATS是最早的基于ARIMA模型的分解时间序列的计算机程序。1994年，Gomez 和 Maravall 将 Tramo 与 SEATS合并，开发了 TRAMO (具有ARIMA噪音、省略观察值和异常值的时间序列回归法)/SEATS (ARIMA时间序列的信号提取法) 程序方法。这是一个包含两个过程的 ARIMA 模型，首先应用 TRAMO 过程预调整每个时间序列的数据，然后将结果传给 SEATS过程获得季节成分。Demetra 软件合并了 X-12-ARIMA和T/S 这两种季节调整方法，是欧洲统计中心支持开发的用于季节调整的特制软件，操作方便，界面友好。

TRAMAO/SEATS 季节调整的一般步骤为：输入数据→原始数据对数处理→在 TRAMO 中观察时间序列 ARIMA 模型最大似然估计和异常值的特殊影响估计→将线性化序列传递给 SEATS→引出各成分的模型→对各成分模型的参数使用Wiener-Kolmogorov 过滤器进行最小平方误差估计→重新引入异常值和特殊影响→输出结果。

（1）使用 TRAMO 自动识别 ARIMA 模型。首先，通过使用均值拟合乘法AR(1) 和 ARIMA (1，1)，选择序列一般有季节部分的差分阶数。然后，选择并拟合 ARMA 模型。最后，根据 BIC 标准进行选择。

（2）TRAMO 自动识别异常值。如有必要同时计算其他回归变量，如交易日变量和复活节变量。TRAMO 可以处理4种异常值：水平移动 (LS)、附加异常值 (AO)、暂时变化异常值 (TC) 和更新异常值 (RP)。程序将在进行离群值探测的样本区间内，对所有的时间点按照 AO、LS 和 TC 这3种类型假设逐个进行回归。如果整个区间的长度为 n，则需要先后引入 3n 个变量，计算每个时点上各类离群值的 t 统计量，根据其显著性判定其是否作为最终的异常值成分加入模型中。所采用的临界值比常规的 t 统计量的临界值大，而且随样本容量的增大而增大。交易日修正是对在月度或季节经济时间序列中循环发生的星期几天数成分影响的修正。复活节影响调整是由复活节引起的经济活动天数变化的调整。我国不存在复活节，此项不需考虑。

（3）TRAMO 将线性化序列传递给 SEATS 做实际的分解。首先，SEATS 估计模型被分解为未观察成分的谱密度函数，假设这些未观察成分为正交的。其次，SEATS 估计趋势周期和经季节调整的参数。被观察的序列需向前预测和向后估计，需使用 Wiener-Kolmogorov 过滤器。然后，异常值和特殊影响被重新引入成分中。TRAMO/SEATS 使用默认2年 (最小8个周期) 的预测长度。

2 我国铁路客运量因素分解和预测的实证研究

2.1 基础数据

铁路客货运量具有明显的线性趋势和季节性特征，适合应用 TRAMO/SEATS 模型进行拟合。2002年1月—2010 年2月铁路客运量月度数据如表1所示，在此基础上对其趋势和季节特征进行具体分析和预测。

2.2 Tramo/Seats 季节调整模型参数设置

（1）对数变换的参数设置。选择 Pretest，即预检验数据是否适用于对数变换。如果初始时间序列中含有零或负值，则不能实施对数变换。

（2）日历效应修正的参数设置。①交易日修正。由于客运量在工作日 (星期一—星期五) 之间和工作日与休息日之间存在区别，并且是否闰年也影响经济活动的活跃性，因此选择 Trading days&Leap-year (7 个回归变量)。此外，选择预检验是否需要交易日 (工作日) 效应修正，允许 Demetra 根据季节调整质量减少交易日回归变量。②国家法定假日修正。每年的劳动节、国庆节和元旦可能对经济活动产生影响，在 TRAMO/SEATS 程序中可进行假日影响的具体日期设置和调整。

（3）异常值及外部变量的参数设置。异常值、外部变量、偏差修正、趋势平滑的参数设置，以及ARIMA 模型、均值修正和实践序列尾部预测的参数设置均为默认选择。

2.3 模型的估计和检验

2.3.1 模型的预调整

对模型采用精确极大似然估计方法进行估计，预调整检验结果如表2所示。通过预调整可知模型通过检验。

表 2 我国铁路客运量预调整模型的检验

（1）我国铁路客运量变动适合于加法模型，即认为时间序列波动的幅度与时间序列的水平不显著相关，计算时无需进行对数变换。

（2）满足 ARIMA 模型的残差服从均值为0的正态分布，无需进行均值修正。

（3）模型未检测出7个交易回归变量的影响，其他交易日和闰年的回归变量影响也不显著。表明工作日内部、工作日与非工作日之间，以及是否闰年对客运量的波动无显著影响。

（4）铁路客运量数据中检测出的显著异常值是2003 年5月，其异常值属于暂时变化和更新异常值(TC)。2003 年5月前后正是北京和香港 SARS 疫情最为严重的时期，对我国铁路客运量产生较大的负面影响，此时客运量为典型的偏小异常值。该异常值影响的回归系数为 -0.479 3。

（5）ARIMA 模型选择中，经过模型识别和比较选择，模型是季节调整中最简便、最强健的 (011)(011) 的 ARIMA 模型，表示经过1次规则性差分和1次季节差分后，该序列成为具有一阶规则性移动平均项和一阶季节移动平均项的平稳序列。

2.3.2 铁路客运量模型的检验

铁路客运量模型的检验结果如表3所示，表明模型通过了所有的检验。

（1）铁路客运量季节调整质量为 1.819，模型在合理区间内，调整质量较好。

（2）模型的异常值比例为 1.02%，在小于 5% 的合理范围内。

（3）模型残差的均值接近 0，并通过0 均值检验。正态性检验表明，残差符合正态分布。偏度和峰度检验表明，模型残差的分布对称，且没有峰值。

（4）残差检验的 Ljung-Box 统计量表明，残差及残差的平方不具有显著的自相关性，残差中不隐含线性和非线性结构。残差检验的 Box-Pierce 统计量表明，残差及残差平方不具有显著的季节自相关性，残差中不隐含季节线性和非线性结构。DW 检验统计量也表明，残差不存在一阶自相关。

（5）ARIMA 模型的拟合标准表明，模型 AIC和 BIC 准则的值都很小，分别为 -235.08 和 -5.62，可见模型具有较好的拟合效果。

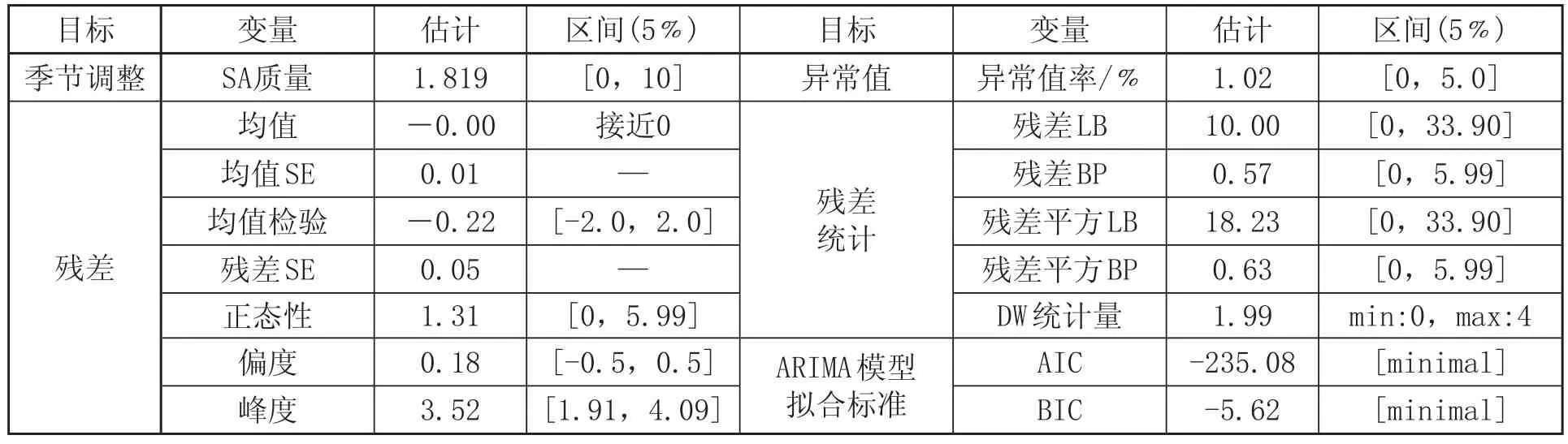
表3 我国铁路客运量季节调整模型的检验

2.4 预测结果分析

模型通过检验后，对 2010 年3月—2012 年2月的客运量进行预测，如表4和图 2、图3所示。由此可见，未来2年内铁路客运量的趋势和季节特征没有显著的变化。计算得到的我国铁路客运量模型预测平均绝对百分比误差 (MAPE) 为 3.755%，模型的预测精确度较高。

2.4.1 趋势性分析

（1）铁路客运量在 2002 年1月—2010 年2月有上升的接近线性的发展趋势，从2007 年8月开始，上升趋势有所减缓。

（2）铁路客运量因 SARS 事件发生暂时脱离趋势的波动，但很快得到恢复。

（3）2002 年1月—2010 年2月，铁路客运量由0.78 亿人增加到 1.42 亿人，增长率为 82.05%。趋势性由 0.804 增加到 1.287，增长率为 60.05%。

2.4.2 季节性分析

剔除趋势因素后，铁路客运量的季节特征为每年2月客运量第一次达到高峰，其季节成分的平均数为 0.096；每年6月客运量第一次达到低谷，其季节成分的平均数为-0.084；在此期间的5月客运量有小幅上升波动，此时季节成分的平均数为 0.003；每年8月客运量第二次迎来高峰，季节成分平均数为 0.174；每年 12 月是客运量的第二次低谷，季节成分平均数为 -0.150；在此期间的 10月，客运量有小幅上升波动，此时季节成分平均数为 0.014。第二次客运量高峰高于第一次，第二次低谷比第一次低谷更低。下半年客运量的波动要比上半年更大。

表4 我国铁路客运量趋势、季节性和客运量预测

3 结束语

目前，国内对具有趋势和季节特征的铁路月度客运量预测的常用方法是 Holt-Winters 模型，本研究在国内首次将 Tramo/Seats 季节调整模型应用于客运量预测领域，与 Holt-Winters 模型相比，季节调整模型引入了预调整模块，对交易日、异常值等进行预调整，使因素分解更精确；分析了客运量历史和将来的趋势、季节特征，而 Holt-Winters模型只能得到末期的上述特征。研究结果表明，模型的预测精度较高。在研究中未涉及有关移动假日的预调整，如春节效应等，还有待进一步研究。

Analysis on Fluctuation of Passenger Traf fi c Volume based on Seasonal Adjustment Model in China

GUI Wen-lin1, HAN Zhao-zhou2

（1. Maths Dept, Huizhou University, Huizhou 516007, Guangdong, China; 2. Statistics Dept, Jinan University,Guangzhou 510632, Guangdong, China）

Based on studying the calculation method of TRAMO/SEATS seasonal adjustment model and the monthly data of railway passenger traffic volume in 2002.1-2010.2 in China, by using the Demetra software, the forecast value of railway passenger traf fi c volume in 2010.3-2012.2 was achieved through the parameter setup, evaluation and inspection of the seasonal adjustment model. Then the paper makes trend and seasonal analysis on the forecast results.The results show that the TRAMO/SEATS seasonal adjustment model has higher forecast precision.

Railway; TRAMO/SEATS Model;Seasonal Adjustment; Passenger Traf fi c Volume

1003-1421(2011)02-0078-05

U293.1

A

2010-07-20

2010-08-31

广东省哲学社会科学基金(09E-04)；广东省自然科学基金(9151051501000066)

责任编辑：付建飞