低渗透储层容易产生高速非Darcy流吗?
2011-01-16李传亮
李传亮
(西南石油大学油气藏地质及开发工程国家重点实验室)

0 引言
符合Darcy方程的流动,称作Darcy流。Darcy流的渗流速度与压力梯度呈线性关系,因此也称作线性流。不符合Darcy方程的流动,称作非Darcy流。非Darcy流的渗流速度与压力梯度呈非线性关系,因此也称作非线性流[1]。Darcy流是层流所致,而非Darcy流则由湍流(紊流)所致,湍流只发生在较高的Reynolds数下,而在生产过程中高Reynolds数对应较高的渗流速度。
与Darcy流相比,高速非Darcy流消耗更多的地层能量,流动效率较低,因此,生产过程中一般应避免出现高速非Darcy流。
现在的问题是,到底是高渗透储层容易出现高速非Darcy流,还是低渗透储层容易出现?高速非Darcy流出现的条件是什么?这是一个没有得到很好解决的理论问题,笔者拟对此进行研究,以便更好地指导生产。
1 非Darcy流
1886年Darcy建立的Darcy方程为[2-3]

式中:q 为流量,m3/ks;A 为岩石渗流截面积,m2;μ为流体黏度,mPa·s;Δp 为流动压差,MPa;ΔL 为岩石长度,m;k为岩石渗透率,D。
式(1)也可以写成微分方程的形式:
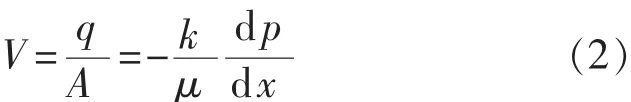
式中:V 为渗流速度,m/ks;dp/dx为压力梯度,MPa/m。
由图1可看出,落在Ⅰ区的数据符合Darcy方程,为 Darcy 流,可用式(1)或式(2)描述,而落在Ⅱ区的数据不符合Darcy方程,为非Darcy流,不能用式(1)或式(2)描述。显然,非Darcy流需要消耗更
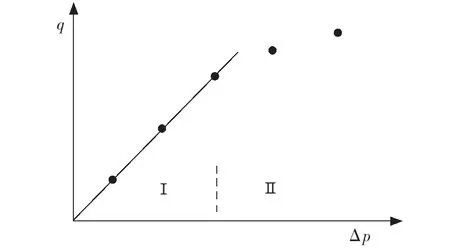
图1 渗流指示曲线Fig.1 Flow index curve
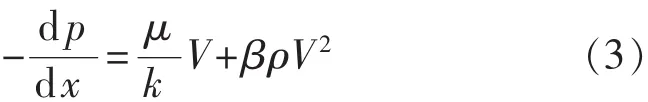
式中:β为非Darcy渗流系数,pm-1,通常称作惯性阻力系数或湍流系数。
由式(3)可看出:当 β=0 时,Forchheimer方程变成Darcy方程,亦即为Darcy流;β的数值越大,非Darcy流越严重;β的大小反映了储层中高速非Darcy流的程度。
β没有理论计算公式,前人的一些实验研究给出了以下形式的统计规律[4]多的能量,才能产生与Darcy流相同的渗流速度或流量。

由图1还可看出,非Darcy流发生在较高的渗流速度条件下。人们通常采用Forchheimer提出的方程描述高速非Darcy流,Forchheimer方程为[4]
另外一些实验结果为[5]

式中:c,m,m1,m2为曲线拟合常数;φ 为孔隙度,%。
式(4)—式(5)显示,渗透率或孔隙度越低,储层越容易产生高速非Darcy流。
2 非Darcy流产生的条件

式中:Re 为 Reynolds数,dless;ρ为流体密度,g/cm3;d为管道直径,m;v为流体速度,m/s。
根据大量的实验结果绘制的阻力系数λ与Reynolds数之间的关系曲线见图2。当Reynolds数较低时,阻力系数与Reynolds数之间呈线性关系,此时为层流。当Reynolds数增大到一定数值后,阻力系数与Reynolds数之间呈非线性关系,此时为湍流。显然,湍流的阻力系数比相同Reynolds数时的层流的阻力系数高,即湍流存在附加的能量损失,二者的阻力系数差为b(图2)。湍流开始时的Reynolds数称作临界Reynolds数。人们通过大量的实验研究发现,管流的临界 Reynolds数大约为 2 000[6]。 湍流与层流的阻力系数满足下式:

非Darcy流是由湍流所致,湍流产生的条件一般用Reynolds数进行判断。管道中流动的Reynolds数计算公式为[6]
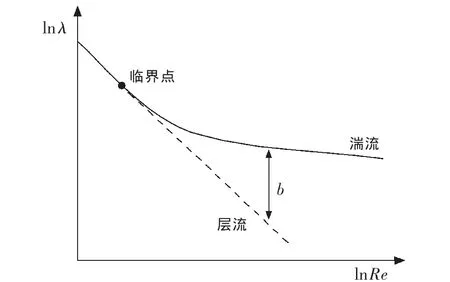
图2 λ与Re关系曲线Fig.2 Curve of relation between λ and Re
式中:λt为湍流的阻力系数,dless;λL为层流的阻力系数,dless;b为湍流与层流的阻力系数差,dless。
很显然,b是Reynolds数的函数,随Reynolds数的增大而增大,可近似写成式中:a为曲线常数;n为曲线指数,n>1。

当流体在多孔介质中流动时,由于流动通道(孔隙)的粗糙度较大,临界Reynolds数大幅度减小。根据实验研究,多孔介质的临界Reynolds数大约在5 以下[7-8]。
流体在多孔介质中的渗流速度由式(2)计算,而真实速度则由下式计算:

式中:v为真实速度,m/ks。
把式(9)代入式(6),得

由式(10)可看出,孔隙直径越小,储层的渗透率和渗流速度越低,Reynolds数就越小,从而越不容易产生高速非Darcy流。因此,高速非Darcy流易于出现在高渗透储层中,这与式(4)和式(5)的实验规律正好相反。
3 Darcy流方程

式中:hf为水头损失,m;L 为管子长度,m;g为重力加速度,m/s2。
把式(11)写成压差的形式:
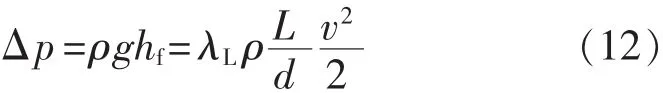
层流状态下管流的沿程水头损失为[6]
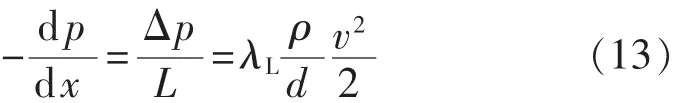
层流状态下阻力系数与Reynolds数的关系满足下式[6]:

再把式(12)写成压力梯度的形式:
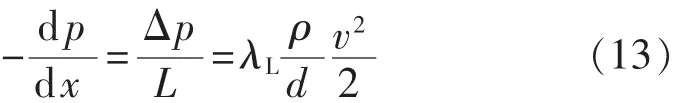
层流状态下阻力系数与Reynolds数的关系满足下式[6]:

把式(14)和式(6)代入式(13),得

把式(9)代入式(15),得
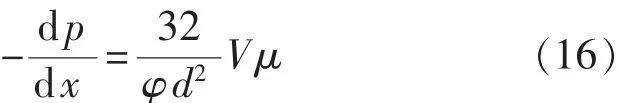
多孔介质的Kozeny-Carman方程可以写成[9]

把式(17)代入式(16),即得到式(2)形式的Darcy方程,因此,Darcy流与层流是相对应的。
4 非Darcy流方程
把式(13)中的 λL换成 λt,得湍流状态下管流的压力梯度计算公式为
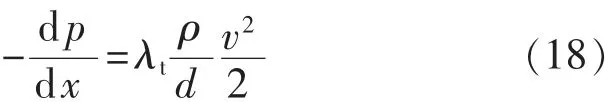
把式(7)代入式(18),得
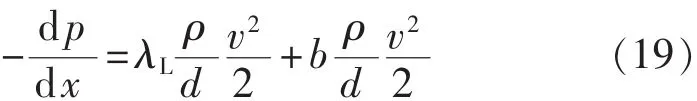
式(19)可以改写成
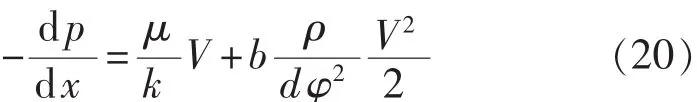
把式(20)与式(3)进行对比,可得

把式(8)和式(10)代入式(21),得
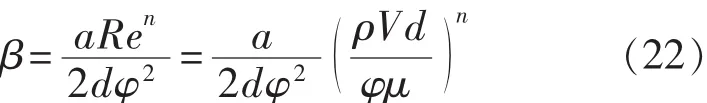
由式(22)可以看出,非Darcy渗流系数β的影响因素较多,并非只是渗透率或孔隙度的函数。孔隙直径越小,渗透率越低,渗流速度就越低,非Darcy渗流系数β的数值也就越小。因此,低渗透储层的高速非Darcy流并不严重,这与式(4)和式(5)显示的逻辑关系正好相反,也说明式(4)和式(5)的实验统计规律不正确。
5 结论
(1)Darcy流对应层流,非Darcy流对应湍流。
(2)高渗透储层容易产生高速非Darcy流,低渗储层不容易产生。
(3)低渗透储层中的高速非Darcy流并不严重。
(4)低渗透储层的流动极其困难,产量极低,生产过程不必考虑高速非Darcy流的影响。
[1]李传亮.油藏工程原理[M].北京:石油工业出版社,2005:46-47.
[2]葛家理.油气层渗流力学[M].北京:石油工业出版社,1982:22-24.
[3]翟云芳.渗流力学:第二版[M].北京:石油工业出版社,2003:10-12.
[4]Dake L P.Fundamentals of reservoir engineering[M].Elsevier Scientific Publishing Company,Amsterdam,1978:255-260.
[5]Jones SC.Using the inertial coefficient,B,to characterize heterogeneity in reservoirrock[C].SPE Annual Technical Conference and Exhibition.Dallas,1987:255-260.
[6]贺礼清.工程流体力学[M].北京:石油工业出版社,2004:139-160.
[7]孔祥言.高等渗流力学[M].合肥:中国科学技术大学出版社,1999:32-34.
[8]Bear J.多孔介质流体动力学[M].李竞生,陈崇希,译.北京:中国建筑工业出版社,1983:95-97.
[9]何更生.油层物理[M].北京:石油工业出版社,1994:42-44.
