圆钢管混凝土不等端弯矩偏压柱工作机理的研究
2011-01-15黄宏杨超张安哥
黄宏,杨超,张安哥
(华东交通大学土木建筑学院,南昌 330013)
圆钢管混凝土不等端弯矩偏压柱工作机理的研究
黄宏,杨超,张安哥
(华东交通大学土木建筑学院,南昌 330013)
利用有限元软件ABAQUS建模,计算了圆钢管混凝土受不等端弯矩偏压时的荷载—变形全过程关系曲线,计算结果与试验结果符合良好。在验证了有限元软件对此类构件模拟的正确性基础上,对此类构件的工作机理进行了分析,并考察了端弯矩比、偏心距、长细比、名义含钢率、钢材和混凝土强度对圆钢管混凝土不等端弯矩偏压柱力学性能的影响规律。研究表明,端弯矩比对构件受力性能有显著影响;偏心距、长细比、名义含钢率、钢材和混凝土强度对构件的影响与其对等端弯矩偏压柱的影响类似。
圆钢管混凝土 不等端弯矩 有限元 承载力 机理
圆钢管混凝土具有承载力高、延性好等优越的力学性能,还具备施工方便及造价经济合理等工程优点,近年来在高层建筑和桥梁中得到广泛应用。实际结构工程中,一般钢管混凝土构件均为偏心受压状态,因此,对钢管混凝土偏压构件进行研究具有实际工程意义。对于钢管混凝土偏压柱,根据顶端和底端弯矩的异同,可分为等端弯矩偏压柱和不等端弯矩偏压柱。本文拟对圆钢管混凝土不等端弯矩偏压柱进行研究。
以往针对圆钢管混凝土等端弯矩偏压力学性能的研究较多[1],而对其不等端弯矩偏压力学性能的研究则相对较少[2-5]。其中,刘殿忠[2]进行了27个圆钢管混凝土柱的不等偏压试验研究;蔡绍怀和顾维平[3]进行了27个两端弯矩不相等的无侧移钢管混凝土框架柱的试验研究;Kilpatrick和Rangan[4]进行了25个高强圆钢管混凝土柱的不等偏压试验研究。另外,丁发兴[5]利用模型柱法对此类构件的承载力进行了计算。
尽管以往研究者在圆钢管混凝土不等端弯矩偏压柱力学性能试验研究方面取得了一些进展,但对其工作机理的理论研究尚少见报道。本文拟采用有限元软件ABAQUS对圆钢管混凝土不等端弯矩偏压柱的荷载—变形关系全过程进行计算,并与其他研究者的大量试验结果进行对比,用以验证有限元软件ABAQUS模拟圆钢管混凝土不等端弯矩偏压柱受力的正确性和可行性,在此基础上,通过典型算例从构件的荷载—变形全过程曲线和对其受力性能的影响因素等方面对此类构件进行分析,以期从理论方面深入认识圆钢管混凝土不等端弯矩偏压柱的工作机理。
1 有限元模型计算
根据圆钢管混凝土不等端弯矩偏压构件的几何与荷载边界条件的不对称性,取全结构模型进行计算。其有限元计算模型,包括材料模型、单元类型和界面接触等参见文献[6-7]。为验证有限元法计算的合理性与可行性,对文献[2-4]中的79个圆钢管混凝土不等端弯矩偏压柱的试验进行了模拟,图1给出有限元对文献[4]中部分算例荷载—跨中挠度曲线的计算结果。可见计算曲线的斜率比试验结果略偏小,承载力和下降段曲线与试验结果符合较好。图2给出了承载力计算结果(Nc)与试验结果(Ne)的比较情况,其比值(Nc/Ne)的平均值为0.928,均方差为0.053。可见,有限元计算结果与试验结果整体符合较好,在本文计算端弯矩比在(-1,1)范围内,采用有限元法对圆钢管混凝土不等端弯矩偏压柱的计算是可行的。
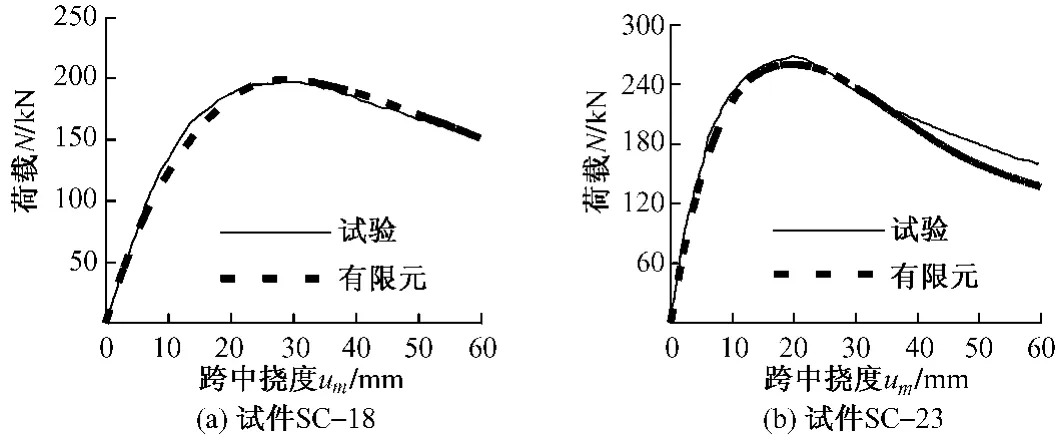
图1 N—um试验曲线与计算曲线的比较

图2 承载力试验与计算结果的比较

图3 典型构件荷载(N)—纵向应变(ε)全过程曲线
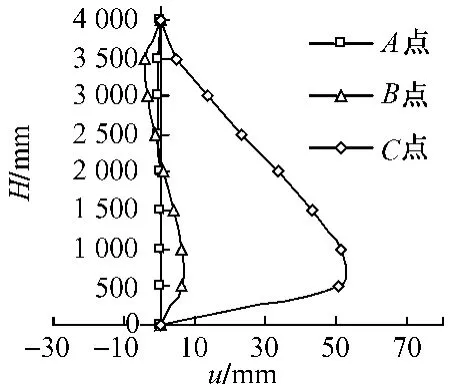
图4 典型构件沿柱高(H)各特征点处挠度(u)曲线
2 荷载—变形全过程分析
为了更好地了解圆钢管混凝土不等端弯矩偏压柱受压工作机理,这里以典型构件为例对其进行分析。所选典型算例的基本参数为:D=400 mm,t=10 mm,L =4 000 mm;采用C60混凝土(fcu=60 MPa)和Q345钢材(fy=345 MPa);端弯矩比β=-1(β=M2/M1,其中M1和M2为构件两端弯矩,需满足|M1|≥|M2|);偏心率e1/r=0.5(e1为M1对应的偏心距,e1=100 mm,r=D/2)。
图3为典型构件荷载—纵向应变全过程曲线,为便于论述,曲线上取了三个特征点,分别是:A点为钢管即将进入屈服阶段的点;B点为构件达到极限承载力的点;C点为纵向应变达到10 000微应变的点。图4为典型构件沿柱高各特征点处对应挠度曲线。图5为各特征点处跨中截面混凝土纵向应力分布情况,应力S33代表纵向应力,图5中,fc为混凝土圆柱体抗压强度。图6为各特征点处钢管的纵向应力分布云图,应力S22代表钢管管壁纵向应力。下面结合图3~图6对荷载—变形全过程曲线的三个阶段进行描述:
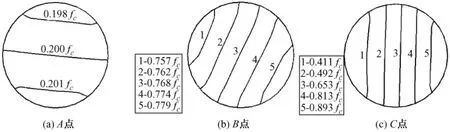
图5 跨中截面核心混凝土各特征点处的纵向应力等值线分布(单位:MPa)
1)OA段:如图3和图4所示,在此低荷载阶段,构件荷载—纵向应变曲线基本呈直线关系,钢管与混凝土均处于弹性阶段。加载过程中,跨中截面核心混凝土全截面处于受压状态,如图5(a)所示,核心混凝土纵向应力分布较均匀,为20 MPa左右。如图6(a)所示,在A点处,钢管仅在顶端出现很小范围的拉应力区,其余部分受压,纵向拉应力仅为32 MPa,钢管底端纵向压应力为344.5 MPa,即将进入屈服。
2)AB段:在此阶段,构件各点挠度曲线呈反对称波形,反弯点位于柱的半高或其附近,如图4所示。混凝土纵向应力继续增长,但未达到圆柱体抗压强度fc(fc=51 MPa),应力等值线大幅转动,如图5(b)所示。此时,钢管拉应力、压应力区都已进入塑性阶段,钢管纵向拉应力、压应力同时增大,压应力区域逐渐减小,拉应力区域逐渐扩展,扩展到纵向截面的1/2,如图6 (b)所示。
3)BC段:在B点之后,随着荷载的增大,挠曲线的反对称性消失,反弯点向加载方向漂移。随着荷载的逐渐增大,更进一步导致沿柱长刚度分布的不对称性加剧,从而反弯点的漂移也随之进一步加剧,如图4所示。在此阶段,随着反弯点的变化,跨中截面混凝土出现一部分纵向应力值增大,而另一部分纵向应力值有减小趋势,钢管纵向应变增长缓慢,构件变形加剧,如图5(c)和图6(c)所示。
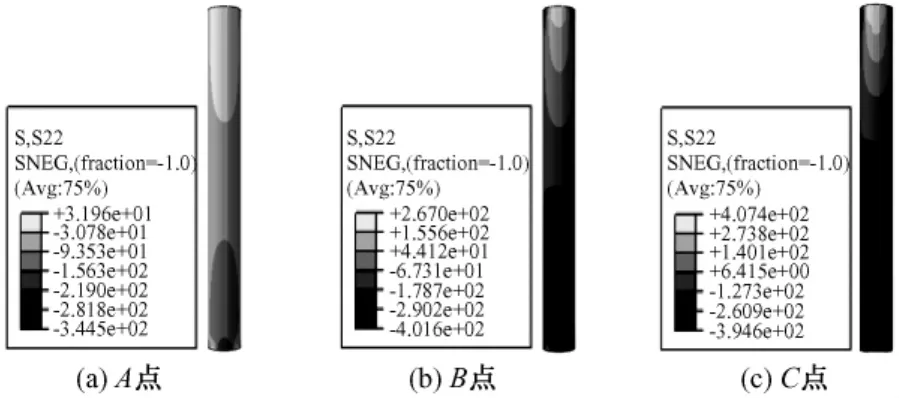
图6 各特征点处横向力作用面钢管的纵向应力(S22)分布云图(单位:MPa)
3 影响因素分析
3.1 端弯矩比的影响
研究表明,端弯矩比对构件受力性能有显著影响,对于端弯矩比从-1到1变化时,构件承载力逐渐减小,延性降低,如图7所示。图8给出了构件达到极限承载力后,承载力下降了25%后的各点沿柱高的挠度曲线。结果表明,在其它条件相同时,所有构件均朝同一侧弯曲,随着端弯矩比从-1到1变化,构件各点的最大挠度逐渐增大,最大挠度点由靠近最大偏心距的一端逐渐向中点移动;对于端弯矩比为1的构件,即为等端弯矩偏压构件时,构件沿跨中截面对称,挠曲线呈明显的正弦半波。产生这一现象的原因是:随着端弯矩比从-1到1变化,构件承受的最大弯矩由柱端向跨中移动,构件挠度增大,因此,二阶效应对构件承载力的影响越来越显著,导致构件承载力下降。

图7 端弯矩比对荷载(N)—纵向应变(ε)曲线的影响
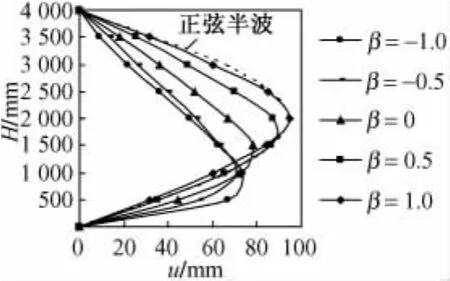
图8 构件各点沿柱高(H)的挠度(u)曲线
3.2 偏心距e1的影响
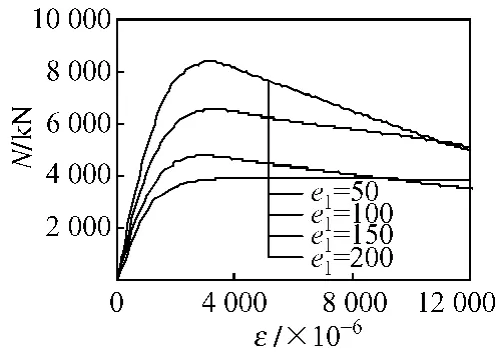
图9 偏心距(e1)对荷载(N)—纵向应变(ε)曲线的影响
图9为偏心距e1不同的圆钢管混凝土不等端弯矩偏压荷载—纵向应变关系计算曲线,e1的变化范围为50~200 mm。结果表明,在其它条件相同时,e1对曲线斜率的影响比较明显,随着e1的增加,承载力峰值点下降,下降段曲线更为平缓。
3.3 长细比的影响
图10为长细比λ不同的圆钢管混凝土不等端弯矩偏压荷载—纵向应变关系计算曲线,λ的变化范围为20~120。结果表明,在其它条件相同时,随着λ的增加,荷载—纵向应变曲线上升,构件的后期延性降低明显。
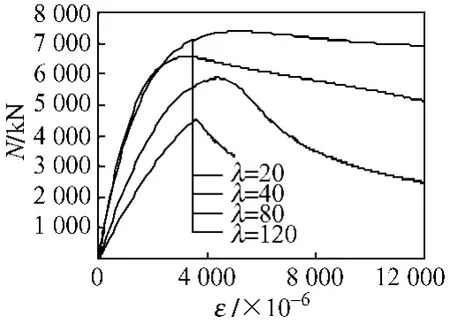
图10 长细比(λ)对荷载(N)—纵向应变(ε)曲线的影响
3.4 名义含钢率的影响
图11为不同的名义含钢率α时,圆钢管混凝土不等端弯矩偏压荷载—纵向应变关系计算曲线,α的变化范围为0.05~0.20。结果表明,在其它条件相同时,随着α的增加,承载力峰值点提高,后期延性差别不大。
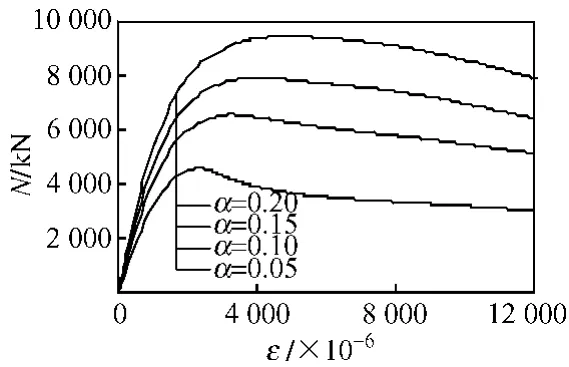
图11 名义含钢率(α)对荷载(N)—纵向应变(ε)影响曲线
3.5 钢材强度的影响
图12为不同的钢材强度条件下,圆钢管混凝土不等端弯矩偏压荷载—纵向应变关系计算曲线,结果表明,在其它条件相同时,其对构件受力性能的影响规律与名义含钢率类似。

图12 不同钢材强度(fy)的荷载(N)—纵向应变(ε)影响曲线
3.6 混凝土强度的影响
图13为不同的混凝土强度条件下,圆钢管混凝土不等端弯矩偏压荷载—纵向应变关系计算曲线,混凝土强度的变化范围为C30~C90。结果表明,在其它条件相同时,随着混凝土强度的提高,其承载力提高,延性降低。
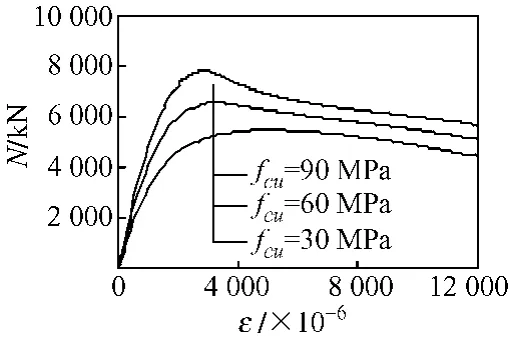
图13 混凝土强度(fcu)对荷载(N)—纵向应变(ε)曲线的影响
4 结语
1)利用有限元软件ABAQUS建模计算得到的圆钢管混凝土不等端弯矩偏压柱荷载—变形关系曲线与文献中的试验结果符合良好,表明本文计算方法是可行的。
2)结合混凝土和钢管的纵向应力分布图对端弯矩比β=-1的典型构件进行分析,分析表明:构件跨中截面混凝土始终承受纵向压应力,而钢管的纵向截面应力分布始终分为拉应力区和压应力区,在构件达到极限承载力的同时,纵向截面拉应力区和压应力区钢管均进入屈服,较充分发挥了钢管的材料强度。
3)端弯矩比对圆钢管混凝土不等端弯矩偏压柱有显著影响,端弯矩比从-1到1变化时,构件二阶效应增加,导致构件承载力显著下降,变形增加,延性降低。
[1]韩林海.钢管混凝土结构——理论与实践(第二版)[M].北京:科学出版社,2007.
[2]刘殿忠.在不等端弯矩作用下钢管混凝土偏压柱稳定承载力的计算[J].哈尔滨建筑工程学院学报,1986,19(1):18-25.
[3]蔡绍怀,顾维平.弯矩分布图形对钢管混凝土无侧移柱承载能力的影响[J].建筑结构学报,1990,11(5):1-8.
[4]KILPATRICK A E,RANGAN B V.Tests on high-strength concrete-filled steel tubular columns[J].ACI Structural Journal,1999,96(2):268-274.
[5]丁发兴.圆钢管混凝土结构受力性能与设计方法研究[D].长沙:中南大学,2006.
[6]黄宏,张安哥.方中空夹层钢管混凝土轴压构件工作机理研究[J].铁道建筑,2008(4):107-109.
[7]黄宏,杨超,张安哥,等.圆钢管混凝土不等偏压的有限元计算[J].华东交通大学学报,2009,26(6):11-15.
TU392.3
B
1003-1995(2011)02-0121-04
2010-09-01;
2010-11-10
国家自然科学基金(51008122);江西省自然科学基金(2009GZC0023)
黄宏(1977—),女,江西樟树人,副教授,博士。
(责任审编 白敏华)
