离心力作用下涡轮转子的径向变形*

房友龙 刘永葆 贺 星

(海军工程大学船舶与动力学院 武汉 430033)

离心力作用下涡轮转子的径向变形*

房友龙 刘永葆 贺 星

(海军工程大学船舶与动力学院 武汉 430033)

为了便于进一步研究叶顶间隙变化规律以及对轮盘和叶片进行强度计算,文章建立了在离心力作用下燃气轮机涡轮转子的径向变形模型。定性分析和定量计算了在不同转速和不同材料的弹性模量下,离心力对转子径向伸长量的影响。并分析了叶片离心力对轮盘变形影响的大小。所得结果表明,离心力引起的转子伸长量正比于转速的二次方;伸长量的变化率正比于转速和角加速度的乘积;且相对于叶片的径向伸长量而言,轮盘的径向变形量更为显著;叶片离心力作用在对轮盘径向变形的作用中占有一定比重;随着轮盘弹性模量增加,离心力引起的转子伸长量减小。

涡轮转子;变形;离心力;应力;应变

Class NumberTK47

1 引言

燃气轮机叶顶间隙对发动机燃油消耗率、工作稳定性及涡轮和压气机的效率和寿命都有重大影响,而发动机运行过程中转子和机匣膨胀变形不匹配是导致间隙变化的主要原因,其中加减速过程中转子的离心力变化是导致膨胀变形不匹配的重要因素[1～2]。所以离心力对叶顶间隙变化的影响是相当大的。且离心力是叶片和轮盘设计和强度计算中必须首先考虑的问题[3～5]。此外,离心力还是影响叶片和轮盘振动的重要因素[3,6]。宋兆泓等[3]在发动机强度设计中计算了轮盘和叶片的离心应力。Howard et al.[7]研究了离心力和科氏力场中旋转叶片和转轴的结构优化。郭军刚等[8]利用ANSYS软件对叶片受离心拉应力的情况进行了数值模拟。侯春宇等[9]推导了等厚轮盘的应力公式并进行了可靠性分析。Kypuros et al.[10]建立了一个计算叶顶间隙的简化模型。岂兴明等[11]改进了文献[10]中叶片和轮盘数学模型,但在轮盘离心力计算中未考虑叶片离心力的影响。

本文根据材料力学的相关理论建立了叶片在离心力作用下的变形和轮盘在叶片离心力和轮盘自身离心力共同作用下的变形模型,对某型舰用燃气轮机的涡轮转子进行了定量计算,所得结论为燃气轮机叶顶间隙变化规律研究、叶片和轮盘的强度校核及涡轮转子的设计提供理论依据和决策参考。

2 叶片在离心力作用下的径向变形

设叶片近似地简化为变截面直杆,如图1,且横截面积沿叶高方向的变化规律为材料单位体积的质量为ρ0。

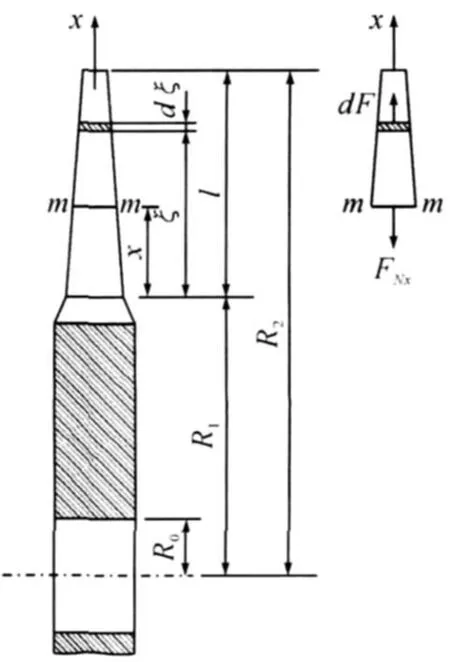
图1 涡轮转子模型

式中:a为由叶片的造型和结构确定的系数,l为叶片高度,x为叶片的计算截面距根截面的距离,A0为叶根截面的面积,A(x)为计算截面 x处的面积。叶根和叶顶的半径分别为R1和R2,转速为n,转子的角速度

由式(4)可知叶片伸长量与ω2成正比。

3 涡轮盘在离心力作用下的变形

假设圆盘等厚,以半径为ρ和ρ+dρ的两个相邻圆柱面和夹角为dφ的两个相邻径向面,从圆筒中取出单元体abcd,如图2,并设单元体沿轴线方向的尺寸(即垂直于图面的尺寸)为一单位。由于变形对轮盘轴线是对称的,故圆盘内半径ρ相同的诸点惯性力相同,沿半径方向的位移u也相同,且与φ角无关。

变形后单元体ad边位移到a′d′,周向应变 εφ和a点沿径向的应变ερ分别为

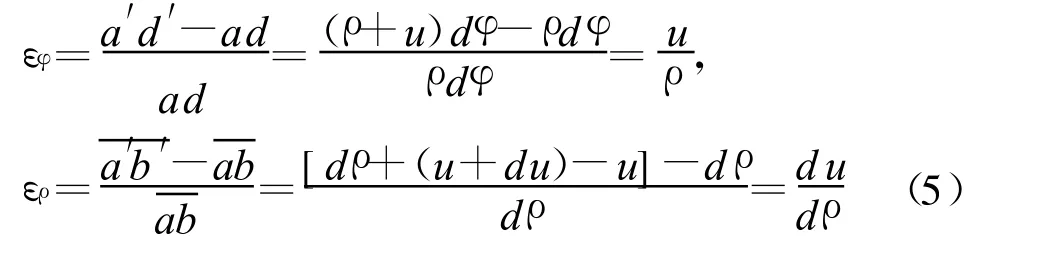
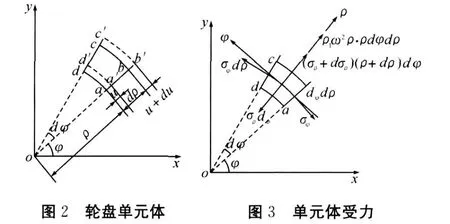
单元体受力如图3所示,作用于单元体的径向应力为σρ,周向应力为σφ。若圆盘的角速度为 ω,材料的密度为 ρ1,作用在ρ方向的惯性力为ρ1ω2ρ· ρ d φ dρ。

将式(5)代入式(8)可求出 σρ和 σφ,将 σρ和 σφ代入式(7),经整理后得出

式中:E为轮盘材料的弹性模量,μ为轮盘材料的泊松比。

利用边界条件确定积分常数。

轮盘在旋转过程中,内缘上不作用外力,外缘上有一周叶片的离心力作用,假设这些惯性力对轮盘的作用均匀分布在外缘上,叶片的个数为z,轮盘厚度为δ。令式(3)中 x=0,得叶片根部截面上的拉力公式FN0。于是边界条件是:ρ=R0时,σρ=0;ρ=R1时 ,

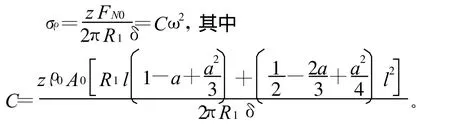
将以上边界条件代入式(11),解出常数A和B并代回式(11)得轮盘应力公式。

将解得的常数A和B代入式(10),令ρ=R1,得轮盘外缘的径向位移量为

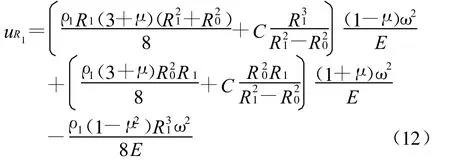
由式(12)可知,轮盘外缘的径向位移量与 ω2成正比。

若不考虑叶片离心力对轮盘的作用,则边界条件是 :ρ=R0 时 ,σρ=0;ρ=R1 时 ,σρ=0,即 C=0。令式(15)中C=0,可求得不考虑叶片离心力对轮盘的作用时轮盘外缘的径向位移量。

于是转子在离心力作用下的总的膨胀量为

式中D1、D2为各自的比例系数。

若已知燃气轮机运行中转速随时间的变化情况,则可得到运行中离心力作用下转子的膨胀变形的情况。

下面分析总膨胀量随时间的变化率。

式中α为角加速度。由上式可知总膨胀量随时间的变化率正比于转速和角加速度的乘积。

4 实例分析

某型燃气轮机高压涡轮转子部分有关参数为:R0=0.087m,R1=0.398m,R2=0.467m,l=0.069m,A0=0.00015m2,取 a=0.59,ρ0=8.22×103kg/m3,ρ1=6.8 ×103kg/m3,E0=2.06 ×1011Pa,E=2 ×1011Pa,μ=0.3,z=86,δ=0.030。

将该型燃气轮机的有关参数代入本文建立的模型中,则叶片和轮盘在离心力作用下的伸长量随转速变化的情况如图4所示。从图4中可以看出随转速增加,轮盘和叶片的膨胀量呈抛物线关系增加,且轮盘的径向膨胀量非常显著。当转速达到10000r/min时,总的变形量为0.63mm,轮盘的膨胀量达到0.54mm,叶片的伸长量为0.09mm,轮盘的膨胀量已是叶片的伸长量的6倍。这一方面是由轮盘本身尺寸大、离心力大导致的,另一方面是由轮盘外缘的叶片离心力的作用所致。

由图5可知,当转速为10000r/min时,考虑叶片离心力作用下的轮盘径向膨胀了0.541mm,而未考虑叶片离心力作用下的轮盘径向只膨胀了0.503mm,叶片离心力作用下轮盘径向膨胀了0.038mm,占轮盘总膨胀量的7%。经计算各转速下叶片离心力作用下轮盘径向膨胀均占轮盘总膨胀量的7%。可见忽略叶片离心力对轮盘的作用求得的轮盘径向膨胀量误差还是很大的。

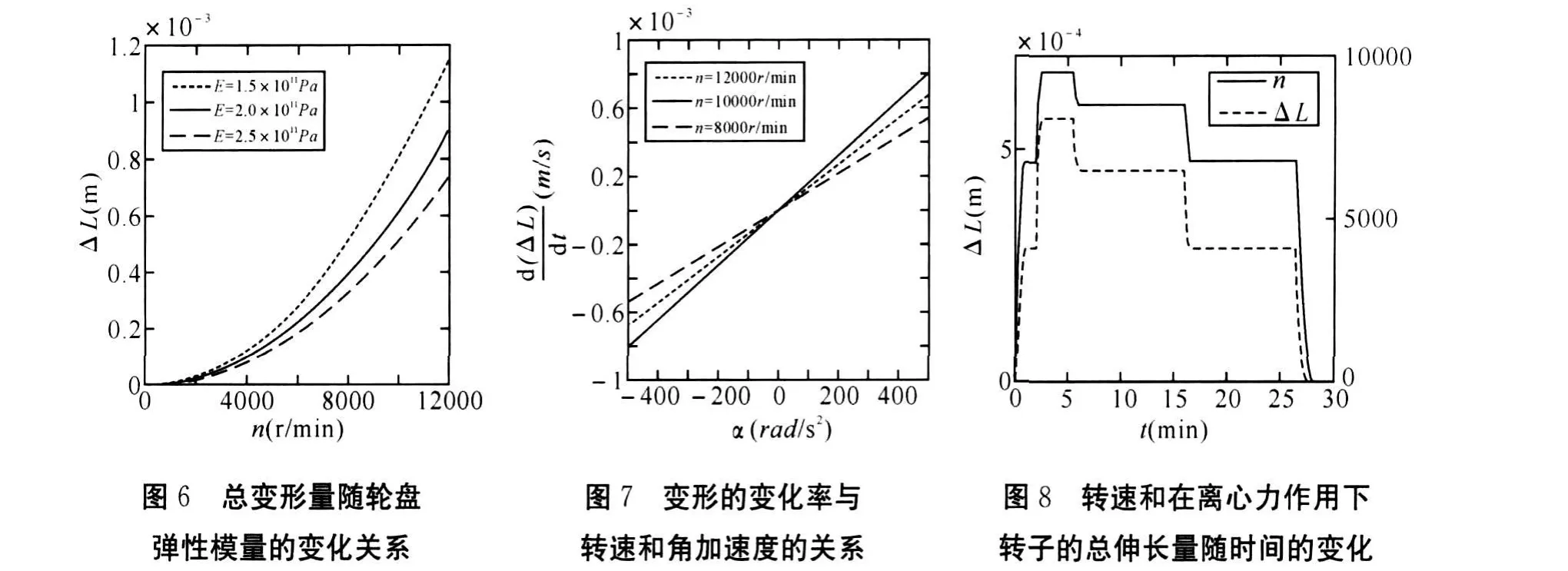
由图6可知轮盘弹性模量越大,转子的变形量越小。当弹性模量由2.0×1011Pa增大到2.5×1011Pa,10000r/min转速时转子总变形量由0.63mm降低为0.52mm,当弹性模量由2.0×1011Pa减小到1.5×1011Pa时,10000r/mn转速时转子总变形量增大为0.81mm。所以如果为避免运行中转子与机匣碰撞摩擦,可增加轮盘材料的弹性模量,减小转子在离心力作用下的径向膨胀量。

由图7可知,转子变形的变化率与转速和角加速度均成线性关系变化。转速为12000r/min时,角加速度由-500rad/s增加到500rad/s,变形的变化率由-0.8mm/s线性增加到0.8mm/s;转速增加,变形的变化率线性增加。

图8显示了转速随时间的变化,并求得离心力作用下的转子总伸长量随时间的变化情况。由图可知当燃机启动后转速在1分钟内达到慢车工况6750r/min,转子伸长了0.29mm;1分钟后燃机在半分钟内加速到全工况9500r/min,转子伸长量由0.29mm迅速增至0.57mm;转速下降为8500r/min时,伸长量降为0.45mm;转速降为零时,转子恢复原态。

5 结语

通过构建离心力作用下涡轮转子的径向变化模型,可得如下结论:

1)离心力引起的转子径向伸长量正比于转速的二次方;伸长量的变化率正比于转速和角加速度的乘积;且相对于叶片的径向伸长量而言,轮盘的径向变形量更为显著。

2)叶片离心力对轮盘的径向变形的作用在轮盘总变形中占据一定比重,不可忽略。

3)随着轮盘弹性模量增加,离心力引起的转子径向伸长量减小。

[1]Lattime S B,Steinetz B M.Turbine engine clearance control systems:current practices and future directions[C]//Joint Propulsion Conference&Exhibit,Indianapolis,Indiana,2002:7～10

[2]Decastro J A,Melcher K J.A Study on the Requirements for Fast Active Turbine Tip Clearance Control Systems[C]//Joint Propulsion Conference and Exhibit,Fort Lauderdale,Florida,2004:11～14

[3]宋兆泓,熊昌炳,郑光华.航空燃气涡轮发动机强度设计[M].北京:北京航空学院出版社,1988

[4]钟芳源.燃气轮机设计基础[M].北京:机械工业出版社,1987

[5]黎明,杨继明,白云.汽轮机转子的应力分析[J].汽轮机技术,2008,50(3):191～193

[6]姚学诗,郑春龙.转子扭转-纵向耦合振动分析[J].力学与实践,2010,32(3):89～91

[7]Howard D G,William J A.Structural optimization incorporating centrifugal and Coriolis effects[J].AIAA Journal,1991,26(10):1743～1750

[8]郭军刚,韩志富,胡丽国,等.涡轮叶片材料非线性应力数值分析[J].导弹与航天运载技术,2007(6):40～44

[9]侯春宇,韩放,王新刚,等.基于等厚涡轮盘结构的可靠性研究[J].机械设计与制造,2009(9):137～139

[10]Kypuros J A,Melcher K J.A reduced model for prediction of thermal and rotational effects on turbine tip clearance[R].NASN/TM—2003-212226,2003,3

[11]岂兴明,朴英,曹志松,等.涡轮叶顶间隙数值仿真[J].计算机仿真,2008,25(6):42～45

Study of the Radial Elongations of the Turbine Rotor with the Centrifugal Effect

Fang Youlong Liu Yongbao He Xing
(College of Naval Architecture and Power,Naval University of Engineering,Wuhan 430033)

In order to investigate the orderliness of the variety of the tip clearance further and calculate the intensity of the disk and blade,the radial elongations model of the turbine rotor with the centrifugal effect was established.Considering different shaft speeds and different elastic moduloes of the disk,the effect of centrifugal on the radialelongations of rotor was qualitatively analysed and quantificationally computed.And the effect of the blade centrifugal on the metamorphose of rotor was also analysed.The results show that the radial elongations caused by the centrifugal are in direct proportion to the square of the shaft speed.The elongation change velocity is proportion to the product of the shaft speed and the accelerated velocity.The radial elongations of the disk are more remarkable than that of the blade.The action of the blade centrifugal on the metamorphose of rotor accounts for certain proportion.The radial elongations of the rotor will decrease as the elastic modulo of the disk increases.

turbine rotor,metamorphose,centrifugal,stress,strain

TK47

2010年8月13日,

2010年9月20日

国家自然科学基金项目资助。

房友龙,男,硕士研究生,研究方向:燃气轮机原理及控制。