一种改进的空域图像信息隐藏算法

彭金虎，玉振明，谢 晴

（1.3.梧州学院 计算机科学系，广西 梧州 543002；

2.梧州学院，广西 梧州 543002）

一种改进的空域图像信息隐藏算法

彭金虎1，玉振明2，谢 晴3

（1.3.梧州学院 计算机科学系，广西 梧州 543002；

2.梧州学院，广西 梧州 543002）

基于可逆矩阵乘法，提出了一种基于LSB的空域图像信息隐藏算法。与基于Arnold置乱的算法相比，本文算法的时间和空间复杂度较低，且有较强的抗攻击能力。

Arnold置乱；可逆矩阵乘法；最低有效位；图像信息隐藏

随着互联网应用的普及，信息安全问题越来越受到重视[1]。作为一种信息安全技术，信息隐藏将秘密信息藏匿于某种任意选定的普通载体信息中，在不被察觉的情况下，通过载体信息的通信过程实现秘密信息的传输[2]。信息隐藏技术可应用于版权保护、图像认证、隐蔽通信等领域，主要的研究内容可分为置乱技术、分存技术、隐藏技术和水印技术等[3]，本文旨在置乱的基础上探讨一种信息隐藏算法。

信息隐藏技术的评价指标包括保真度、容量、鲁棒性、安全性和不可见性等[4]，文献 [5-7]所述基于Arnold变换的方法均较好地达到了上述目标。文献 [2，3，5，10]对Arnold变换进行了讨论，该变换有期周期性，对N×N图像，其置乱周期TN≤N2/2， N＞2[8]， 如 128×128 图像的变换周期为96，256×256图像的变换周期为192[6]。基于此，本文提出一种基于可逆矩阵变换的图像信息隐藏算法。算法先使用可逆矩阵对秘密信息进行置乱，再将其隐藏于载体图像的低四位LSB中[9,10]。提取秘密信息时，根据密钥确定秘密图像的隐藏区域并对该区域进行逆置换，再提取隐藏于LSB中的信息，最后还原秘密图像。该算法避免了Arnold变换的周期问题，无需迭代或循环，一次变换就可以得到较好的置乱效果，有效提高了算法的效率。

1 位平面与LSB

图像I可看成一个矩阵，每个矩阵元素对应一个像素，每个像素可以有一个或多个颜色分量，即：

所有像素的同一分量的相同位组成一个平面，即位平面 （分别叫第i号位面，i=1,2,…,8），其中，高位平面对图像视觉质量起主要作用，低位平面作用不明显。实验表明，最低3个或4个位平面的数据被修改，图像失真情况可满足普通隐蔽通信的要求[9]。

LSB，Least Significant Bit，即最低有效位。基于LSB的方法是空间域信息隐藏方法中的经典方法，也是变换域信息隐藏常采用的方法。该类方法将秘密信息隐藏在载体信息的一个或多个LSB之中。根据人眼的视觉分辨能力，隐藏在LSB中的秘密信息具有较好的不可见性[1]。

2 置乱算法及安全性

2.1 秘密图像置乱算法

在秘密图像矩阵S中，对于元素S（x,y），将（x,y）看成一个一行两列的矩阵。为方便计算，假定S是方阵，且|S|=L。根据矩阵乘法原理，在模L的情况下，可以对 （x,y）右乘一个二阶可逆矩阵A，将其映射到矩阵 （x1,y1），即：

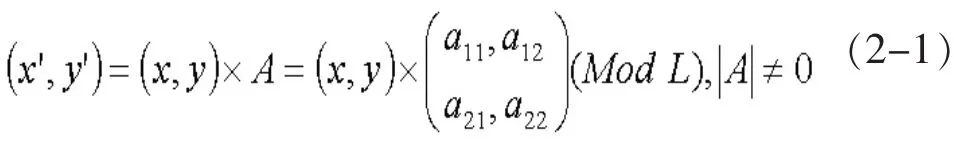
令 X＝a11×a22-a21×a12， 有如下情况：（1） 当 A为单位矩阵E时，该变换无置乱效果；（2）当A=k×E时，该变换对S作平移变换；（3）当X=-1时，该变换对S作对称变换；（4）当|X|（绝对值）为非零偶数时，该变换是一对多变换；（5）当副对角线上有零元素且主对角线元素之积为奇数时，该变换将S的一行映射到S″的一列，并在列内打乱顺序 （或反之），置乱效果不好；（6）当|X|是奇数时 （如X=1），该变换为双射，可用于对S置乱[5]。此时， 遍历 S 中所有像素， 且令 S1（x1,y1）=S（x,y）， 即可得到置乱图像S1（如图1所示）。

图1 置乱前后像素对应关系示意图

2.2 置乱算法的安全性

置乱过程中，a11、a12、a21、a22是置乱的密钥。展开 （2-1）式可得如下方程组：

讨论方程 z= （x×a11+y×a12）（mod L）， 取 a11＝5，a21＝10，L=256，则z的函数图像如图2所示。

图 2 函数 z=（5x+10y）（mod 256）的图像

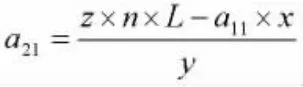
根据2.1中的结论，为使|A|是奇数且副对象线上无0元素，在a11和a21的三种奇偶组合中（“偶+偶”组合不可能），“奇+偶”组合下，攻击者猜中 a12和 a22的概率为 4/（n0× ne）；“奇+奇” 组合下攻击者猜中 a12和 a22的概率为 8/（n0× ne）。 故攻击者猜中 a12和 a22的概率小于等于 12/（n0× ne）。

3 基于LSB的信息隐藏算法

3.1 隐藏算法

本算法要求载体图像I大于等于秘密图像S，设载体图像中隐藏信息的区域的水平偏移为R、竖直偏移为C，则可以通过在I（R+x1,C+y1）的低四个LSB上隐藏S（x,y）的高四位来完成对S的隐藏[9]。其中R、C、L是隐藏密钥，密钥空间大小与R+1、C+1之积成正比。步骤如下 （如图3所示）：

图3 隐藏过程示意图

3.2 抗攻击处理

攻击者可以对载密图像的局部像素属性进行分析，从而确定有无秘密图像存在[11]。隐藏秘密图像之后，本文向载密图像的非隐藏区域引入一定噪声，以降低攻击者成功定位信息隐藏区域的概率。

记rect（x，y）表示矩形主对角线上两个点的坐标分别为x和y； 坐标为x＝u，y＝v的点记为 （u，v）；对矩形区域r设置噪声的方法记为SetNoise（rcet （r）∈ [0,7]。 引入噪声的过程为：

4 隐藏信息提取算法

根据密钥R、C和L确定载密图像中隐藏信息的分布区域Ih，并对 （2-1）式左右两边均右乘A的逆矩阵 A-1， 即从（x1,y1）还原出原始位置 （x,y），即：

5 实验结果

5.1 信息隐藏与提取实验结果

根据上述算法，设秘密图像大小L为300，载体图像大小也为300，偏移R、C均取0。实验中，秘密图像、载秘图像和恢复图像如图4-6所示。

图4 秘密图像

图5 载秘图像

图6 恢复图像

根据文献 [12]所介绍的失真度量方法，采用ITU-R Rec.500图像主观评估指标对载秘图像评估，其品质度量级别可达 “良好”级；采用平方误差均值MSE度量，其度量值为38.2049；采用峰值信噪比PSNR度量，其度量值为32.3096。采用标准互相关度量恢复出的图像与秘密图像的NC值为0.9973。

5.2 鲁棒性实验

为了验证算法的鲁棒性，对载秘图像实施不同攻击，并对攻击后的图像提取信息，结果如图7-9所示。当载秘图像被剪切左上角1/4区域后，本算法可还原出如图7所示图像；在强度为0.1的椒盐噪声攻击下，算法提取到如图8所示图像；在强度为0.00002的高斯噪声攻击下，可得到如图9所示图像。从上述还原实验结果看，本算法在上述攻击下可正常提取秘密信息，本算法有较强的鲁棒性。

图7 1/4剪切

图8 0.1椒盐噪声攻击

图9 0.00002高斯噪声攻击

6 总结

本文提出了一种基于可逆矩阵乘法的图像信息隐藏算法。该算法避免了Arnold变换周期的出现，时间复杂度和空间复杂度均为基于Arnold变换的算法的1/TN，TN为变换周期。若基于Arnold变换的算法采用逆变换还原图像[3]，本文算法的复杂度为其1/n，其中n为置乱迭代次数。本算法在隐藏信息之前先对秘密图像进行置乱，秘密信息分散在载体图像中，有利于提高抗攻击性。隐藏信息后，本文向未隐藏信息区域引入噪声，可一定程度上提高算法鲁棒性。本算法隐藏信息的位平面固定，易于实现秘密图像的盲提取。同时，攻击者要确定 R、C、L、a11、a12、a21、a22才能攻击成功， 其概率约为 R/（R×C×L× （n0×ne）2。

[1]Huaiqing Wang,ShuoZhong.Cyber Warfare：Steganography vs Steganalysis[J].Communigations ofthe acm,2004（10）.

[2]王向阳,陈利科,赵红.一种新的DCT域图像水印嵌入算法[J].辽宁师范大学学报：自然科学版,2005（1）.

[3]董梅,高康林.矩阵奇异值分解和Arnold置乱技术在图像隐藏中的应用[J].山东大学学报：理学版,2005（3）.

[4]PIERRE MOULIN,RALF KOETTER.Data-HidingCodes[J].PROCEEDINGSOF THE IEEE,2005（12）.

[5]黄良永,肖德贵.二值图像Arnold变换的最佳置乱度[J].计算机应用,2009 （2）.

[6]司银女,康宝生.基于改进的Arnold变换的数字图像置乱[J].计算机技术与发展,2008 （2）.

[7]贾松浩,等.一种改进的Arnold变换[J].河南大学学报：自然科学版,2009（2）.

[8]丁玮,闫伟齐,齐东旭.基于Arnold变换的数字图像置乱技术[J].计算机辅助设计与图形学学报,2001（4）.

[9]Abbas Cheddad,JoanCondell,KevinCurran.Digital image steganography：Surveyand analysis ofcurrent methods[J].Signal Processing,2010（90）.

[10]王国新,平西建,张涛.空域LSB信息伪装及其隐写分析[J].计算机工程,2008（1）.

[11]王朔中,张新鹏,张卫明.以数字图像为载体的隐写分析研究进展[J].计算机学报,2009（7）.

[12]杨义先,钮心忻.数字水印理论与技术[M].北京：高等教育出版社,2006.

An Improved Information Hiding Algorithm in Spatial Domain of Images

Peng Jinhu1,Yu Zhenming2,Xie Qing3
（1.3.Department of Computer Science,Wuzhou University,Wuzhou 543002,China）
（2.Wuzhou University,Wuzhou 543002,China）

On the basis of invertible matrix multiplication,an information hiding algorithm in spatial domain of images based on LSB is proposed.Compared with the Arnold-based algorithms,the proposed algorithm needs less time and requires lower level of space complexity.

Arnold-based scrambling;invertible matrix multiplication;LSB;image information hiding

TP309

A

1673-8535-（2011）02-0078-05

2010-11-13

国家自然科学基金项目（61062014）；广西壮族自治区教育厅科研项目（200708MS057）

彭金虎（1981－），男，四川省三台县人，梧州学院讲师，硕士研究生，主要研究方向：图像处理、网络安全。

玉振明（1963－），男，梧州学院副院长，教授，博士，主要研究方向：数字信号处理。

谢晴（1981-），女，梧州学院讲师，硕士研究生，主要研究方向：图像处理。

高 坚）