随机多孔介质中的不混溶驱替

王

（武汉纺织大学 数学与计算机学院，湖北 武汉 430073）

随机多孔介质中的不混溶驱替

（武汉纺织大学 数学与计算机学院，湖北 武汉 430073）

对随机多孔介质中粘滞指进的分形性质进行研究，建立正方网格来模拟多孔介质中润湿流体的侵入和流动，运用决定论模型进行研究。结果表明，多孔介质的几何拓扑强烈地影响了粘滞指进的结构和驱替过程。粘滞指进图像扫及面积随着迭代次数n的增加而增大。增加迭代次数n和网格尺寸，会导致驱扫效率E的增大。

多孔介质；逾渗集团；粘滞指进；驱扫效率

随机多孔介质中流体的输运在许多工程领域都有重要的应用。例如土壤中的有害废物的扩散，石油工程中油的移动，色谱的分离和催化过程等。关于粘滞指进问题的第一个理论分析是由 Saffman 和 Taylor[1]针对Hele-Shaw[2]装置进行的。均匀网格中的两相流已有大量研究结果[3]。本文把多孔介质用正方网格中逾渗集团表示，运用决定论模型[3]对随机多孔介质中的粘滞指进分形问题进行研究。

1 模拟方法

我们视多孔介质为正方网格，格点表示孔隙，喉管表示通道，称为键。如图1所示，当格点取值为0时(座(i+1,j))，该点不连通，此时与之相连的所有的键均完全封闭(图1中与座(i,j)相连的右键，或图2中的a或f键)，即导流率g(i,j),(i-1,j)=0；当格点取值为1时(图1中的座(i,j),(i-1,j),(i,j-1)和(i,j+1))，除其近邻为0的座外，与之相连的所有的键均完全导通，g(i,j),(i-1,j)≠0等等。

对于后一类键又有三种情况：已完全被驱替流体所占据(图1中与座(i,j)相连的左键，或图2中的d键)，该键两端点的压力p均为1；已部分被驱体流体所占据(图1中与座(i,j)相连的上键，或图2中的c键)，该键一端点的压力p为1，另一端点的压力p小于1；完全没有被驱体流体所占据(图1中与座(i,j)相连的下键，或图2中的b键)，该键上完全充满被驱替流体，且一端点的压力p为1，另一端点的压力p小于1。还有一种键的状态是，该键本身导通，但其两端的格点的压力均小于1，即驱替流体尚未流到这些格点(或图2中的e键)。

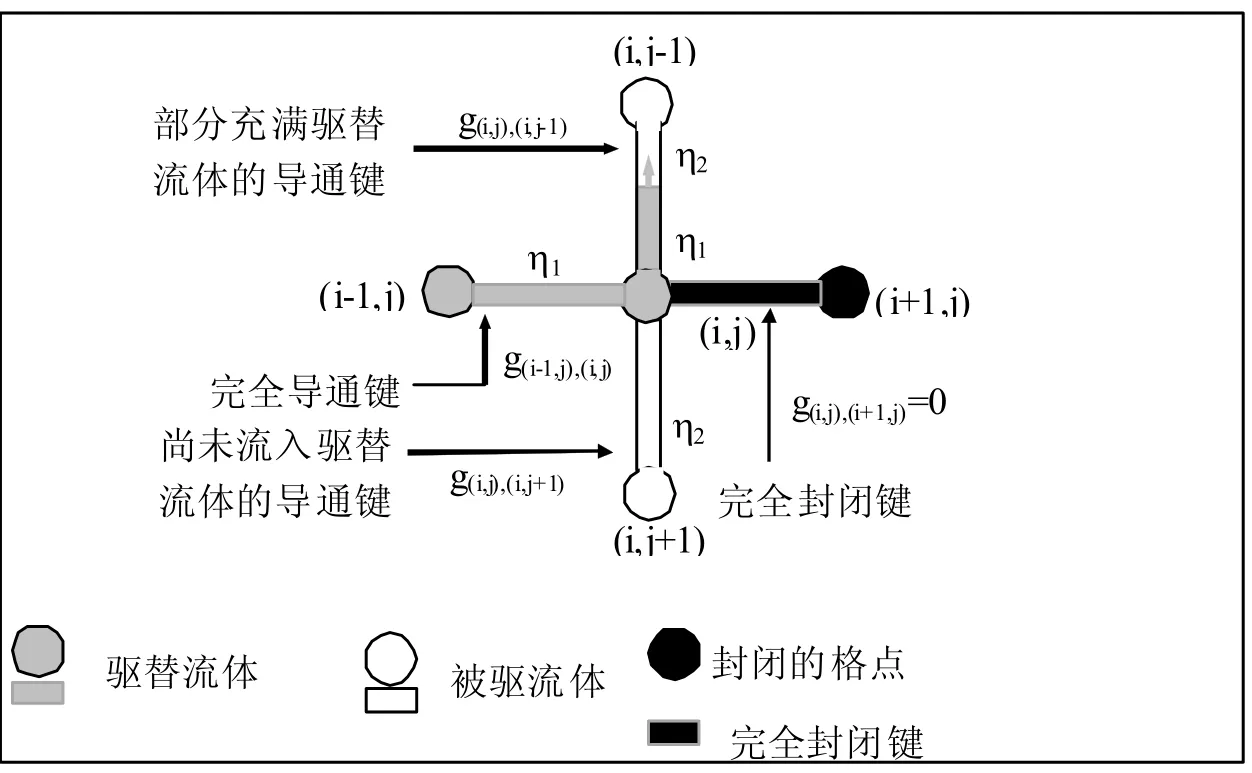
图1 网格中流体流动状态示意图

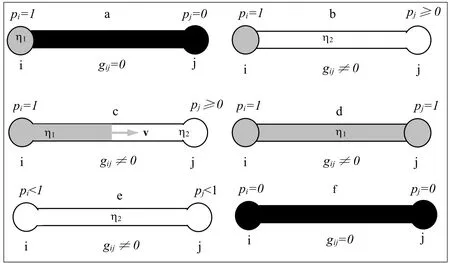
图2 网格中座键状态示意图

在201×201正方网格中，给定一个逾渗概率P，若P≥0.59，则存在一个跨越集团；当P=1时，格点的占有率为100%，对于不同的P对应于不同连通性的孔隙介质。对于不属于跨越集团的格点和集团，它对应沉积岩的不连通区域。我们的模拟仅在跨越集团中进行。为此，我们建立孔隙介质和两相流的模型如下：不同逾渗概率P的逾渗集团对应不同的孔隙介质，视格点为孔隙，键为喉管，且喉管的半径是非均匀分布的：r→(r-rmin)/(rmax-rmin)，rmin和rmax分别是喉管半径的最小和最大值。在参考文献[4,5,6]曾运用过类似的模型。

因此，对于任意一个喉管i，其半径ri在0-1之间。例如图3(a)是一个5×5的正方网格，假设网格中心为流体注入点。驱替规则如下：每一步，依照逐次超松弛技术只有一个喉管充满驱替流体与被驱替流体。图 3(b)显示了图 3(a)第一次驱替的过程。假设当驱替流体到达逾渗集团的边界时凝集。为了模拟凝集的破坏性，我们假设每个被注入流体的喉管的尺寸随着下面的规则增加[7]: ri→ri+∈(1-ri)，其中∈表示取0-1之间的随机数。这样做使得ri(t+1)总是在[ri(t), 1]之间变化。在某种意义上也就是说，喉管的半径随着驱替流体凝集的密度而变化。

例如图 3(c)表明了 3(b)驱替后被破坏的多孔介质。充满凝集流体的喉管半径遵循下面的公式ri→ri+∈(1-ri)，并且介质完全干缩，这时候新的驱替流体进入。依照对r的一般假设，ri(t)的最大值是1，跟rmax的取值无关。比如，如果喉管的半径为最大值rmax，那么经过凝集破坏后的半径增加到rmax+ ε (ε ＞ 0)。这时，r→[(rmax+ε )-rmin)]/[ (rmax+ε )-rmin)。我们研究当P从0.6到1变化时201×201网格中的逾渗，迭代次数直到n=20。

图3 驱替凝集过程示意图

由Poiseuille定律，通过两个相邻格点i，j之间键中的流体流量为

我们采用逐次超松弛技术从方程(1)和(2)中解出压力场

这里，超松弛系数ω为1.66。边界条件为：在注入点p = 1，在网格外周界p = 0。在确定了压力之后，驱替流体的前锋移动一段位移

在一个界面相邻的格点，我们选择各键中驱替前沿最先到达下一个格点所需时间（即各键驱替时间中最短的那一个）为时间步长Δt。然后，按照相应的时间步长Δt移动两相流的交界面并引入新的交界面，计算压力场，重复整个过程，直到到达外部边界为止。这种方法的主要优点是我们可以对驱替过程进行研究，也被称为决定论模型[8]。

2 多孔介质的粘滞指进生长

图4表明了在5种迭代次数下（n=1,2,5,10,20），逾渗集团中粘滞指进的图像（P = 0.8，M = 10）。n = 1时的粘滞指进图像已经在参考文献[9]中研究过了。当n ＞ 1时，驱替流体扫及范围随着参数n的增加而增大，而当n ≥ 10时，粘滞指进图像的形状几乎没有改变了。而且，改变迭代次数不会影响逾渗集团中粘滞指进的各向异性。这个结果说明多孔介质的几何拓扑结构很强地影响了粘滞指进的形状和结构。

图4 逾渗集团（201×201网格）中粘滞指进图像

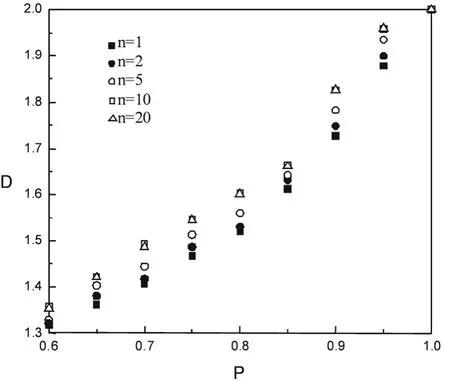
图5 分形维数D与逾渗概率P的函数关系图

为了研究多孔介质的几何拓扑结构对粘滞指进图像的形状和结构的影响，本文得到了粘滞比 M=10，不同逾渗概率P及不同迭代参数n下的粘滞指进图像，并计算出其分形维数D。首先测量不同网格L×L ，不同迭代次数n，以及不同概率P下粘滞指进图像中驱替流体扫及面积S，假定[4]: S ～ LD。在图5显示了粘滞指进图像的分形维数D与逾渗概率P之间的关系。当P=1时，无论迭代几次，分形维数D=2。也就是说，在二维正方网格中粘滞指进图像的结构依赖于有限的粘滞比M。当n=10及n=20时，粘滞指进图像的分形维数D和P无关，也就是说，当n ≥ 10时，粘滞指进的结构是稳定的。由图像可以看出，分形维数D随着P的增加而增加，与迭代次数n无关。这表明，多孔介质的几何拓扑结构对粘滞指进有很大影响。

3 驱扫效率

研究多孔介质粘滞指进现象的一个特别有实用价值的方面就是驱扫效率E，它是预测驱替性能的一个重要参数。在现场驱替过程中，体积驱扫效率定义为：E=驱扫体积/总体积。由于现在我们研究的是随机多孔介质中的粘滞指进，因此，此时的效率应为面积驱扫效率，设扫及面积为Ae扫及区域内多孔介质的面积为As，于是有[8]

式中L为网格尺寸。该式表明分维D能够被合理地作为评价驱扫效率和石油储量的有用参数。

图6显示了驱扫效率E与网格尺寸L之间的函数关系。由图可以看出增加迭代次数n和网格尺寸L，驱扫效率E随之减小，当L达到最大值时E有最小值。图中每条E～L曲线都存在有两个线性区域，分别表示粘滞指进的凝集区域和驱替区域[10]。

图6 驱扫效率E与网格尺寸L的函数关系图

4 结论

本文中，我们把随机多孔介质看做是正方网格，借助于决定论方法在喉管半径为非均匀分布的假定下，模拟了粘滞指进在逾渗集团中的一些新的性质。逾渗集团中粘滞指进扫及面积的大小随着迭代次数n的增加而增大。当n ≥ 10时，粘滞指进图像几乎不再变化。增加逾渗概率P导致分形维数D的增加，与迭代次数n无关。这表明多孔介质的几何拓扑结构严重影响了粘滞指进。驱扫效率E随着迭代次数n和网格尺寸L的增加而减小，当网格尺寸L取最大值时，E达到最小。并且在网格尺寸L的整个变化过程中，E～L存在两种线性关系，分别表示粘滞指进在逾渗集团中的凝集区域和驱替区域。

[1] P. G. Saffman, G. I. Taylor. The Penetration of A Fluid into A Porous Medium or Hele-show Cell Containing A More Visous Fluid[J].Proc. Royal Society A, 1958, 245: 312-329.

[2] H. S. Hele-Show. The Flow of Water[J]. Nature, 1898, 58: 34-36.

[3] M. Sahimi. Flow Phenomena in Rocks[J]. Reviews of Msdern Physics, 1993,65: 1393-1534.

[4] E. Salmon, M. Ausloos, N. Vandewalle. Aging of Prous Mdia Fllowing Fuid Ivasion, Feezing and Tawing[J]. Physical Review E,1997, 55: R6348-52.

[5] K. T. Tallakstad, H. A. Knudsen, T. Ramstad. Steady-State Two-Phase Flow in Porous Media: Statistics and Transport Properties [J].Physical Review Letter, 2009, 102: 074502.

[6] Ch. Cottin, H. Bodiguel, A. Colin. Drainage in two-dimensional porous media: From capillary fingering to viscous flow [J]. Physical Review E, 2010, 82: 046315.

[7] J. P. Tian, K. L. Yao. Ageing of Random Porouse Media Following Fluid Deterministic Displacement, Freeing, Thawing[J]. The European Physical Journal B, 2000, 14:543-549.

[8] H. Siddiqui, M. Sahimi. Computer Simulations of Miscible Displacement Processes in Disordered Porous Media[J]. Chemical Engineering Science, 1990, 45: 163-182.

[9] J. P. Tian, K. L. Yao. Computer Simulations of Two-phase Flow with Surface Tension in The Percolation Cluster[J]. Physics Letters A, 1999, 251: 259-261.

[10] H. Boularot, G. Albinet. Frozen and Active Regions in Diffusion Limited Aggregation Clusters[J]. Physical Review E, 1996, 53:5106-5110.

The Immiscible Displacement in Random Porous Media

WANG Man
(College of Mathematics and Computer Science, Wuhan Textile University, Wuhan Hubei 430073, China)

In this paper, the fractal nature of Viscous fingeringin (VF) random porous media has been studied. The fluid transport is based on the deterministic method. The result shows that the topology and the geometry of the porous media have a strong effect on displacement processes. The cluster size of viscous fingering pattern in percolation cluster increases with the increase of iteration parameter n. When iteration parameter n ≥ 10, VF pattern does not change with n. The distribution of velocities normal to the interface of VF in percolation cluster is also studied. The sweep efficiency E increases along with the increasing of iteration parameter n and decreases with the network size L.

Porous Media; Percolation Cluster; Viscous Fingering; Sweep Efficiency

O189.11

A

1009－5160(2011)06－0090－05

王嫚（1986-），女，硕士研究生，研究方向：无序空间中的分形生长.