基于Matlab液面银薄膜分形维数的计算分析

陈苗根，陈小军，余森江，焦志伟

（中国计量学院 物理系，浙江 杭州 310018）

基于Matlab液面银薄膜分形维数的计算分析

陈苗根，陈小军，余森江，焦志伟

（中国计量学院 物理系，浙江 杭州 310018）

利用Matlab数值分析软件，将沉积在液体基金的银薄膜真彩数值图像进行了二值化处理，并计算了该银薄膜的分形盒维数。经计算发现银薄膜图像灰度分布具有双峰结构。二值化后的图像计算得到液体基底金属银薄膜的盒维数大约为1.50，计算结果与相关文献的结果一致。它表明基于Matlab的盒维数算法用于计算此类液体基底金属薄膜的二维分形盒维数具有较好的准确性, 同时也表明其可以用来分析液体基底表面其他金属薄膜分形维数。

二值化；分形盒维数；银薄膜

1 引言

近年来，分形的研究受到非常广泛的重视，其原因在于分形既有深刻的理论意义，又有巨大的实用价值。分形向人们展示了一类具有标度不变对称性的新世界，吸引着人们寻求其中可能存在着的新规律和新特征［1］。而另一方面，分形结构是广泛存在在制备的金属薄膜中，引起了人们极大的关注，成为当今的研究热点之一。因此，我们希望找到一种简单可靠的方法并用计算机模拟计算并分析液体基底表面金属薄膜［3-5］的分形特征。

计算薄膜的分形维数，分形维数的定义有很多种，为了简单方便我们选用计算起来最为简单的盒维数。在计算盒维数之前，一般原图像都是真彩图像，这样的图像直接处理是不合适的，这就涉及到图像的灰度处理和二值化，真彩图像转化为灰度图像十分容易，但二值化就较为繁杂了，选择一种合适的二值化方法是至关重要的，对薄膜分形盒维数结果有这巨大的影响［2］。二值化图像的分形盒维数计算就方便多了，分形盒维数的原始定义用计算机实现起来难度很大，但它有一些等价定义更适合于应用。此时，选用好的算法和一种简单的编程语言能使结果准确并缩短课题研究的时间。

2 编程原理和思想

2.1 编程原理

对实验用显微镜所拍真彩图像进行分形计算必须要分二步进行，分别是图像二值化处理和分形数值拟合。这里分形数值分析采用分形盒维数方法，两种方法简介如下：

图像二值化是图像灰度变换的一种特殊情况，是为了从图像中抽出对象形状的最基本的处理方法［2］。一般我们手中的都是真彩RGB图像，首先应将其颜色成分去掉，获得灰度图像。从灰度图像变换到二值图像最重要的就是阈值处理。以某一阈值T为界，把图像的灰度级转换成0或1的操作就是阈值处理。在阈值处理中最关键的就是确定图像的阈值，在特殊情况下，阈值T对整幅都是定值时，叫做固定阈值处理。

分形盒维数又称计盒维数［1］，是应用最广泛的维数之一，它的普遍应用主要是由于这种维数的数学计算及经验估计相对容易一些。

设F是Rn上任意非空的有界子集，Nδ（F）是直径最大为δ，可以覆盖F的集的最少个数，则F的下、上盒维数分别定义为

如果这两个值相等，则称这共同的值为F的盒维数，记为

盒维数有一些等价定义，有时这些定义更适合应用。考虑Rn中δ-坐标网立方体，即下列形式的立方体：

其中m1，…，mn都是整数，在计算盒维数时，可以等价地取Nδ（F）为与F相交的边长为δ的网立方体的个数。

由于计算机的像素并不是无限小的，因材，在用计算机编程计算平面图像盒维数时，可以由函数logNδ（F）相对于-logδ图的斜率来估计。

2.2 程序流程

本文选择Matlab软件作为编程工具，其具有强大的图像处理和数值分析功能，对原始图像二值化后，用如下类似于文献6的流程来计算分形盒维数：

图1 盒维数计算流程

3 验证及计算

3.1 程序验证

为了验证上述分形盒维数计算方法的正确性，对一些已知分形维数的图形，我们首先对直线和正方形的分形进行了计算。直线分形盒维数计算结果是1.0078与理论值1.00误差0.78%，正方形是2.0152与理论值2.00误差0.76%，如图2。我们对Koch雪花曲线和Sierpinki地毯也进行了计算，计算结果显示koch曲线是1.2613，与理论值1.2618误差0.039%，Sierpinki地毯是1.8930，与理论值1.8928误差0.0106%，如图3。以上验证结果说明基于Matlab环境下，该程序的分形盒维数计算是相当准确和稳定的。

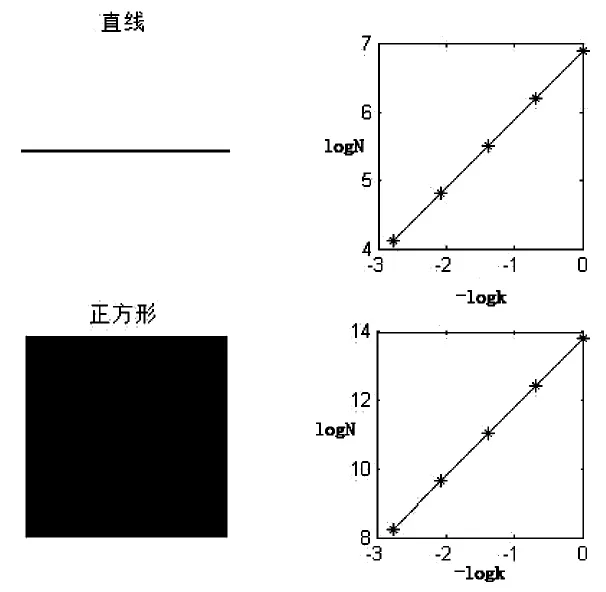
图2 直线和正方形的分形拟合曲线

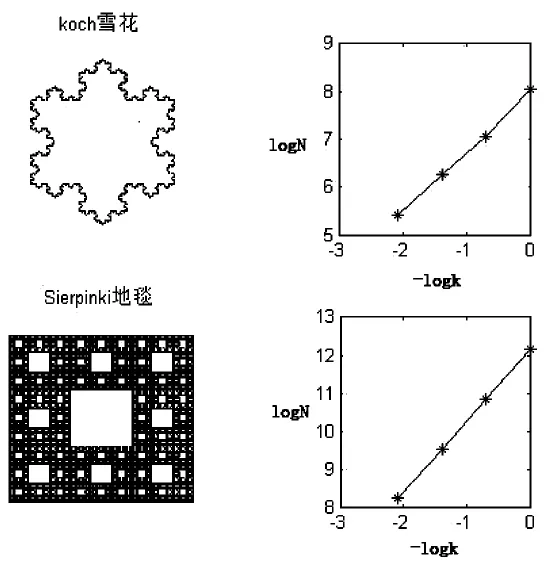
图3 Koch雪花和Sierpinki地毯的分形拟合曲线

3.2 银薄膜图片二值化及分形维数计算

图4a显示了一张典型的液体基底表面银薄膜的灰度图像，图4b是图4a的灰度级分布图，从中可以看出其图像其具有明显的双峰结构，第一峰为图4a显灰色液体基底格点数（灰度值为100左右），第二峰为图4a显白色的银薄膜的格点数（灰度值为255左右）。该结果说明了该银薄膜与液体基底有明显的对比灰度，也说明了采用光学显微镜可以准确地分辩银薄膜和液体基底。

然后，我们将阈值设定在双峰之间的合适值，这里将阈值设定为175（即灰度值为175），将银薄膜的灰度图像二值化。二值化后的图像如图4c所示。最后，我们根据图1流程图计算得到该液体基底表面银薄膜分形维数大约为1.50，如图4d。该计算结果与相关文献［4］的结果一致，也说明了该算法可用于计算此类液体基底表面金属薄膜具有较好的准确性，预示着可以用来计算液体基底表面其他金属薄膜如铜薄膜［5］，铁薄膜［6］等分形维数。

图4 液面银薄膜及其分形维数

4 结论

1）用直线、正方形、Koch曲线和Sierpinki地毯验证表明用Matlab编程计算分形盒维数是足够准确的。

2）液体表面银薄膜的灰度级具有双峰结构。计算结果说明了采用光学显微镜可以准确地分辩银薄膜和液体基底。

3）液体表面银薄膜的分形维数大约为1.50，计算结果与相关文献的结果一致，表明该算法用于计算此类液体基底表面金属薄膜的二维分形盒维数具有较好的准确性。

［1］张济忠.分形［M］.北京：清华大学出版社，1995，122-127.

［2］高木干雄，下田阳久主编，孙卫东等译.图像处理技术手册［M］.北京：科学出版社，2007.1227-1229.

［3］Gao-Xiang Ye，Thomas Michely，Volker Weidenhof，Inés Friedrich，Matthias Wuttig，Nucleation，Growth，and Aggregation of Ag Clusters on Liquid Surfaces，Phys.Rev.Lett. ［J］，1998，81，622.

［4］Miao-Gen Chen，Jian-Ping Xie，Gao-Xiang Ye，Formation mechanism and ordered patterns in Cu films deposited on silicone oil surfaces，Phys.Lett.A ［J］，2006，360，323.

［5］Quan-Lin Ye，Sen-Jiang Yu，Jin-Sheng Jin，Gao-Xiang Ye，Formation mechanism and orderly structures of an iron film system deposited on silicone oil surfaces，Chin.Phys.Lett.［J］，2003，20，1109.

［6］杨书申，邵龙义，MATLAB 环境下图像分形维数的计算［J］.中国矿业大学学报，2006，35（4），478.

An Analysis of Fractal Dimensions of Silver Films on Liquid Substrates Based on Matlab

CHEN Miao-gen，CHEN Xiao-jun，YU Sen-jiang，JIAO Zhi-wei
(Department of Physics,China Jiliang University,Hangzhou 310018,China)

Based on the Matlab data analysis software,we binarizate the color image of the silver films deposited on the liquid substrates firstly,and then calculate the fractal box dimension.It is found that there are two peaks in the gray scale distribution of the image of the silver film. The fractal box dimension of the silver films on the liquid substrates is about 1.50,which is consistent with the reference reported before.It indicates that the program of the fractal box dimension based on the Matlab has good accuracy and it can be used to analyze other metal films on the liquid substrates.

image binarization;fractal box dimension;silver films

周小莉）

O484.1

A

1672-3708（2011）03-0020-05

2011-04-08；

2011-06-01

国家自然科学基金项目（10802083）、浙江省自然科学基金项目（Y6090542）

陈苗根（1981- ），男，浙江玉环人，博士，副教授，主要从事薄膜物理研究。