分支井渗流-应力耦合场分析

魏臣兴，练章华，丁亮亮，郭衍茹，韩 涛

（西南石油大学“油气藏地质及开发工程”国家重点实验室）

分支井渗流-应力耦合场分析

魏臣兴，练章华，丁亮亮，郭衍茹，韩 涛

（西南石油大学“油气藏地质及开发工程”国家重点实验室）

在多孔介质的渗流过程中，存在着极强的流固耦合作用。针对广泛使用的分支井型，在利用COMSOL Multiphysics软件时充分考虑流固耦合作用，分析耦合渗流场和应力场的分布特点，同时通过运用三维库伦准则计算失效系数fail值来判断井壁岩石的危险截面，并进一步计算出不同造斜率情况下失效系数fail的最小值和失效系数fail≤-2.5 MPa区域的体积积分值，从而研究采用不同造斜率侧钻分支井眼对井壁失效区域大小的影响。结果表明，在单渗流场分析中采用定压缩系数方法得到的孔隙度其变化微乎其微，而耦合渗流场中的孔隙度、渗透率在井底附近区域变化明显。因此，考虑流固耦合作用下的渗流场能更真实地反映地下渗流情况。在耦合应力场分析中，Von Mises等效应力的最大值和失效系数fail最小值均出现在侧钻分支井窗口处，即窗口处井壁岩石为危险截面，进而得出在取造斜率为15°/30 m进行侧钻分支井眼的情况下井壁岩石失效范围最小的结论，为分支井的设计和施工提供了理论依据。

分支井；渗流场；应力场；流固耦合；数值模拟；井壁稳定

0 引言

油藏数值模拟分析方法经历了从单渗流场研究到耦合渗流场研究的历程。单渗流场研究只考虑渗流场而忽略了应力场的作用，随着计算机技术的发展，耦合研究特别是流固耦合作用越来越受到重视。经流固耦合研究发现，在油藏的开采过程中，地层中各种力处于一种动态平衡状态，地层孔隙压力发生变化，引起岩石骨架有效应力的改变，岩石骨架发生变形，进而导致了孔隙度、渗透率等物性参数的改变；同时，渗流场中物性参数的变化又会影响地层孔隙压力的重新分布，最终将影响地层流体的渗流和开采动态。有研究表明，油藏开采过程中存在极强的流固耦合作用，是不可忽略的［1］。

前人研究应力场的作用时，虽通过采用随定值压缩系数变化的孔隙度来表征应力场对渗流场的影响［2］，但本文计算结果表明采用此方法孔隙度变化甚微，近似为常数，而实际地层中的孔隙度和渗透率应为地层有效应力的函数。笔者采用广泛使用的分支井井型［3］，并充分考虑渗流场与应力场耦合作用下渗流参数将随岩石应力状态不同而发生改变，来分析侧钻分支井开窗处的渗流场和应力场特点，同时应用三维库伦准则，判断井壁岩石易于失稳的危险截面，以及从主井眼侧钻分支井眼的造斜率对井壁危险截面的影响。

1 数学模型

1.1 渗流场数学模型

为了研究流固耦合渗流场的特点以及耦合场中井壁岩石的应力分布情况，假设岩石孔隙为不可压缩单相流体所饱和，整个渗流过程是稳态的且等温的，建立起流固耦合渗流的数学模型为［1，4-6］

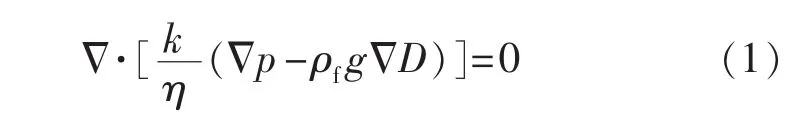
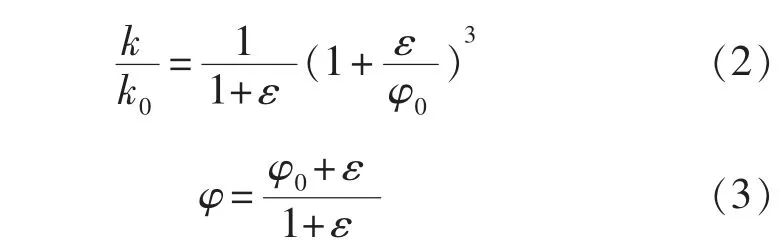
为了研究侧钻分支井眼处的流场，根据模型的具体情况给定不同的边界条件：

供给边界

井底

对称边界和上、下边界

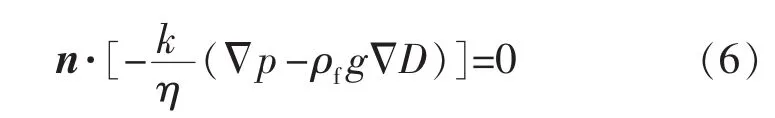
1.2 应力场数学模型

作用于地层岩石上的体积力主要是重力和渗透体积力（∂p/∂x，∂p/∂y，∂p/∂z）［2］。 这些力在压降没有传递到供给边界期间是随时间发生变化的，但压降传递到供给边界后则慢慢趋于稳定。分析过程中描述地层岩石骨架变形的基本方程为

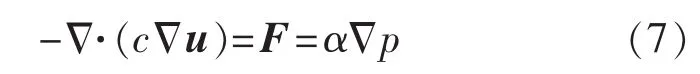
根据Shaybah油田所钻裸眼分支井情况［3］，模型边界条件如下：

供给边界

对称边界

上边界

下边界

井底

1.3 库伦判断准则

在渗流-应力耦合场中，采用3D库伦准则，充分考虑3个主应力和地层孔隙压力的影响，来判断危险截面，见式（13）

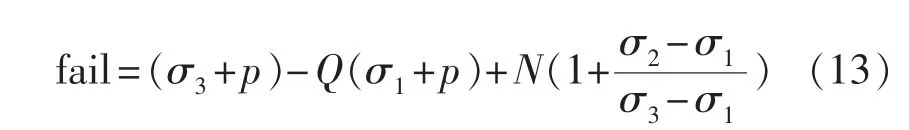
其中

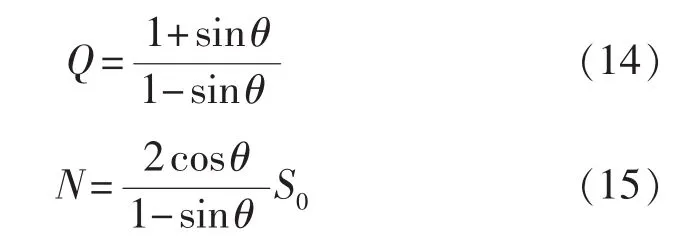
利用式（13）得到fail值，进而判断井壁岩石的状态，其中fail为正值时表明岩石处于稳定状态；fail为负值时表明岩石易于失效，且负值越大，失效的可能性越大。

2 耦合场分析

COMSOL Multiphysics是一款基于有限元理论的直接以偏微分方程为研究对象的多物理场耦合软件，具有求解耦合问题的强大能力。将式（1）与式（7）2种微分方程在该软件中进行耦合计算，分析垂深1500 m处侧钻分支井眼区域在生产压差4.7 MPa的条件下的渗流场分布（图1）。图1中流线显示渗流方向，流线上颜色代表压力的分布情况，切面上颜色代表压力梯度的变化，在地层流体向井底渗流的过程中，压力从供给边界到井底的变化表现为明显的“压降漏斗”形式，这一趋势在图2的切线图中表现得更为明显。图2是以侧钻分支井眼的窗口处为0 m，向井深方向，间隔20 m，取出井眼剖面上横向的压力分布情况，后续的切线图也是在相同位置处取值。图1中切面图上压力梯度的分布和图2压力切线图中的“压降漏斗”表明压力主要消耗在井底附近，这与数值求解得到的结论一致［2］，说明此模型的研究方法是正确合理的。

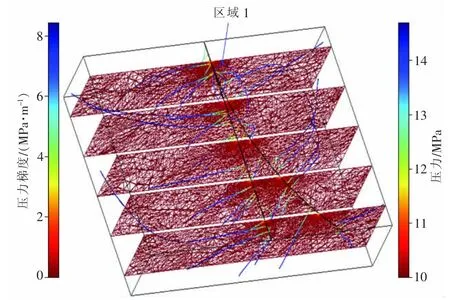
图1 20°/30 m分支井渗流场分布图Fig.1 The seepage field distribution of 20°/30 m

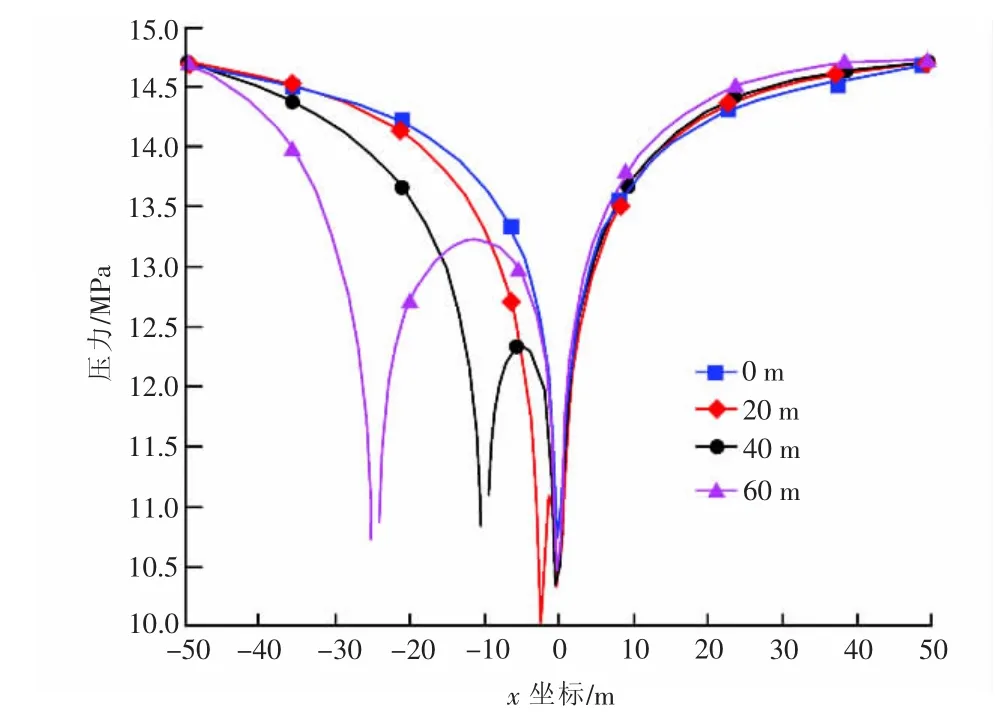
图2 分支井压力切线图Fig.2 Pressure distribution of lateral wells

在图2中，沿井深方向距侧钻点20 m，40 m和60 m处，由于主井眼和分支井眼横向距离的加大及井间干扰作用的减弱，两井眼之间的压力也在逐渐恢复；在分支井中存在分支井眼的一侧，由于供给边界的限制，分支井眼的“压降漏斗”更为陡峭。在不同深度条件下，分支井中不存在分支井眼的一侧，由于距离分支井眼较远，其横向分布的压力受井间干扰引起的压降不明显，即侧钻分支井对驱动该区域的地层流体意义不大，分支井眼仅对侧钻分支井眼的一侧作用效果较好。因此，在地层压力衰竭的油田或薄油层开展老井侧钻，最好是采用双分支井或多分支井，以提高油井控制区域的压力波及能力，从而实现增产增注。

在耦合渗流场分析中，岩石骨架颗粒在渗透体积力和重力的作用下其力学行为发生改变，在渗流场中反映为地层的孔隙度和渗透率随着应力场作用程度的不同而发生相应的变化［7-11］，见图3、图4所示孔隙度、渗透率变化曲线（在分析中所采用初始孔隙度为25%，初始渗透率为10 mD）。结合图2中的压力分布情况对图3、图4中的物性参数分布趋势进行分析。在供给边界附近，由于地层孔隙压力变化不大，因而所引起的岩石变形相对也比较小，在达到稳定渗流状态时，岩石的孔隙度和渗透率变化不大，与初始孔隙度和渗透率相当；而在靠近井底附近区域，孔隙压力急剧变化，所引起的岩石变形也相当显著，对岩石的物性参数影响十分明显。总的来说，在分析区域内，孔隙度、渗透率变化趋势与“压降漏斗”相对应。而采用不考虑应力场影响的单渗流场分析时，在分析程序中嵌入孔隙度随定值的孔隙压缩系数变化的表达式如下

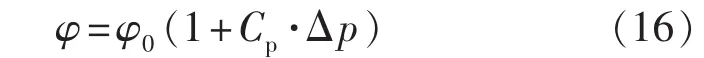
经计算可知，孔隙度值的改变微乎其微，基本上为初始常数，见图3中虚线所示。将其与耦合渗流场分析得到的参数进行对比，可见耦合渗流场分析得到的孔隙度、渗透率要小于单渗流场分析得到的参数，特别是在井底附近。由于孔隙度、渗透率的减小，整个地层的压力分布将大于仅考虑渗流场时的压力分布，且渗流速度也相应地减小，最终将影响整个油藏的开发动态［12］。

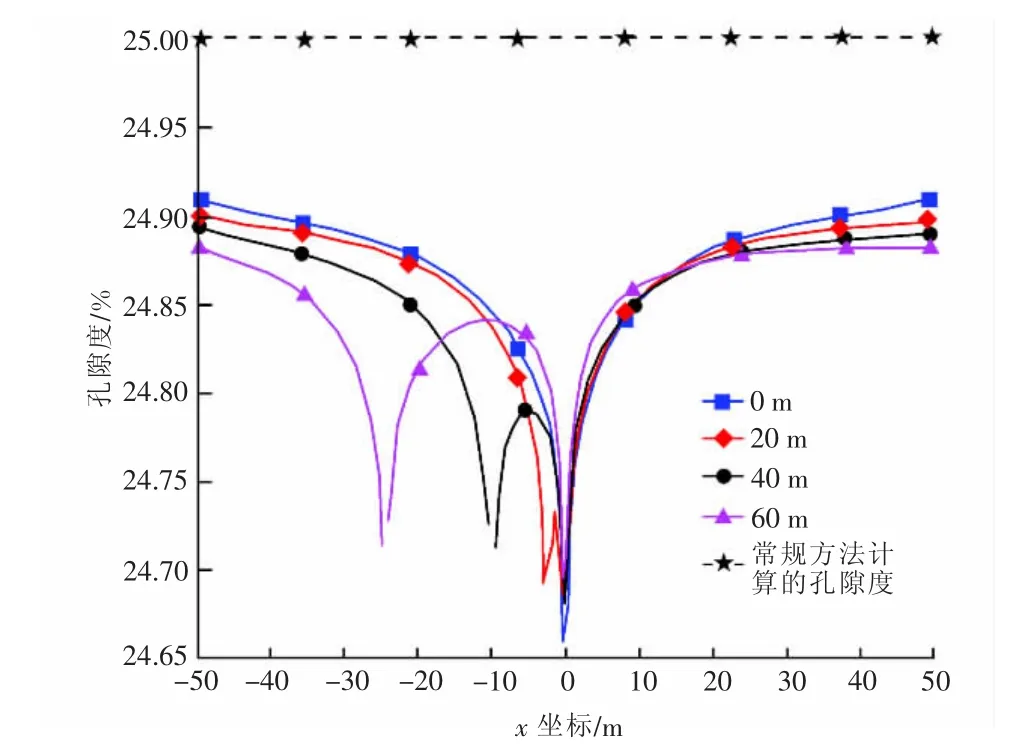
图3 耦合渗流场中孔隙度分布图Fig.3 Porosity distribution in coupling seepage field

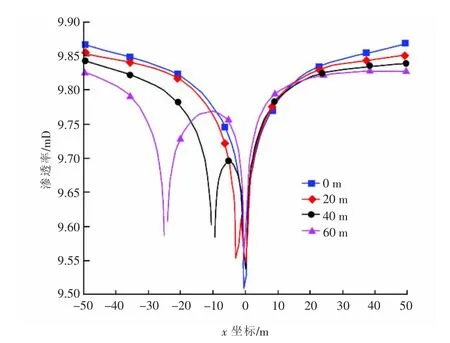
图4 耦合渗流场中渗透率分布图Fig.4 Permeability distribution in coupling seepage field

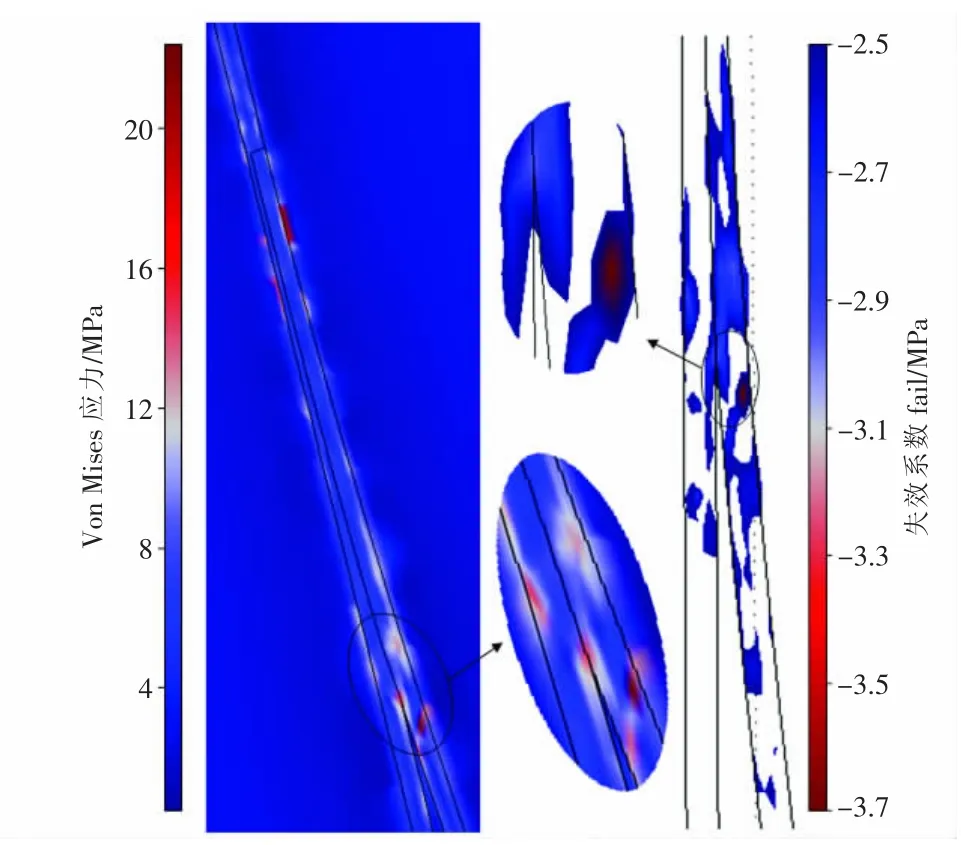
图5 图1所标示区域1处应力和失效系数局部分布Fig.5 Local distribution of stress and fail coefficient of region 1 showed in Fig.1

图5为图1中所标示区域1处应力场和失效系数fail的局部分布图。根据材料的第四强度理论计算的Von Mises等效应力最大值22.5 MPa出现在窗口附近的井壁处；同样失效系数fail值在井壁附近负值较为集中，其最小值处也就是最易发生井壁不稳定的截面，同时也正是在侧钻分支井眼的窗口处。在不考虑井壁岩石内化学作用的前提下，单从力学方面分析，侧钻分支井眼窗口附近的井壁岩石极易垮塌。因此除非岩石结构极为稳定，否则在侧钻分支井中，应对侧钻分支井眼的窗口附近加强完井质量，将其周围封固好，最好将分支井的完井级别提高到3级以上，以便可用井下连接工具实现分支井眼和主井眼的机械连接，从而提高不稳定地层的连接强度，防止窗口附近区域于生产过程中在渗流场和应力场耦合作用下发生事故，提高安全生产时间，延长油井寿命［13］。

3 造斜率对井壁稳定性的影响

在研究主井眼中侧钻分支井眼的造斜率对井壁稳定性的影响时，考虑到分支井眼造斜率一般要求在（10°～20°）/30 m，并结合国内实施的分支井情况，分别取造斜率为 5°/30 m，10°/30 m，15°/30 m，20°/30 m 及 25°/30 m 来加以研究［14-16］。

造斜率对失效系数fail的影响如图6所示。随着造斜率的增加，fail系数最小值是曲折变化的，在模型考虑的造斜率范围内，造斜率为15°/30 m时取得较大值。也就是在地层因素相同的条件下，其它造斜率相对于15°/30 m时的造斜率更易出现井壁不稳定问题。取fail系数≤-2.5 MPa的严重失效区域进行体积积分，可以得到各个造斜率条件下井壁不稳定的范围大小。如图6所示，在造斜率为15°/30 m时的体积积分取得较小值。因此，考虑到现有侧钻分支井的工具设备以及井眼轨迹控制能力，在满足采油工艺的前提下，对于主井眼中侧钻分支井最好采取15°/30 m的造斜率为宜。

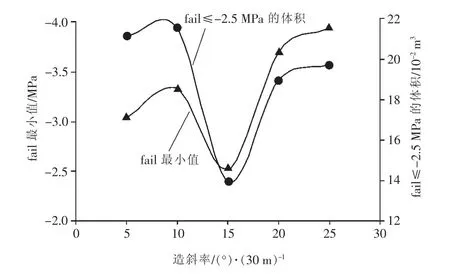
图6 造斜率对fail系数和fail≤-2.5的区域体积的影响Fig.6 The impact of build-up rate on fail coefficient and volume integration in the condition of fail≤-2.5

4 结论

（1）耦合渗流场的压力分布与常规数值求解结果分布趋势大致相似，但耦合渗流场中的孔隙度和渗透率是变化的，更能反映真实地层渗流。

（2）在应力场作用下，地层岩石的孔隙度、渗透率急剧减小，进而影响渗流场和油藏的开采动态，其中耦合渗流场各点处的压力大于单渗流场分析得到的压力，耦合渗流场的速度小于单渗流场的渗流速度。

（3）分支井窗口处的井壁最不稳定，最好能将分支井的完井级别提高到3级以上，以便提高不稳定地层的连接强度，避免井下事故的发生。

（4）主井眼中侧钻分支井眼的造斜率不同，对井壁的危险程度影响较大。考虑到现阶段的钻井能力，侧钻分支井眼时取造斜率为15°/30 m最为合适。

符号说明：

p——地层孔隙压力，MPa；

pr——供给边界压力，MPa；

Δp——地层孔隙压力变化值，MPa；

pw——井底压力，MPa；

p0——上覆地层压力，MPa；

p1——模型顶界处骨架应力，MPa；

p2——井底岩石所承受的外压，MPa；

η——动力黏度，mPa·s；

D——相对于基准面，计算区域的位置水头，m；

φ——孔隙度，%；

k——渗透率，mD；

φ0——初始孔隙度，%；

k0——初始渗透率，mD；

ε——岩石的体积应变；

Cp——岩石压缩系数，取1×10-6，MPa-1；

ρf——地层流体密度，kg/m3；

n——边界的单位法向向量；

u——模型中x方向位移，m；

v——模型中y方向位移，m；

w——模型中z方向位移，m；

u——位移矢量u，v和w；

F——力矢量；

c——系数；

α——有效应力系数；

θ——岩石内摩擦角，（°）；

S0——岩石内聚力，MPa；

σ1——第一主应力，MPa；

σ2——第二主应力，MPa；

σ3——第三主应力，MPa；

fail——判断井壁是否失效系数，MPa。

［1］胡永乐，冉启全，孙建平.流固耦合油藏数值模拟［M］.北京：石油工业出版社，2007：3-98.

［2］李晓平.地下油气渗流力学［M］.北京：石油工业出版社，2008：35-59.

［3］Dossary A S，Saudi Aramco，Mahgoub A A.Challenges and Achievements of Drilling Maximum Reservoir Contact（MRC） Wells in Shaybah Field［R］.SPE 85307，2003.

［4］李允.油藏模拟［M］.东营：石油大学出版社，1999：37-49.

［5］赵延林，曹平，赵阳升，等.双重介质温度场-渗流场-应力场耦合模型及三维数值研究［J］.岩石力学与工程学报，2007，26（增2）：4024-4031.

［6］盛金昌.多孔介质流-固-热三场全耦合数学模型及数值模拟［J］.岩石力学与工程学报，2006，25（增 1）：3028-3033.

［7］樊怀才，李晓平，窦天财，等.应力敏感效应的气井流量动态特征研究［J］.岩性油气藏，2010，22（4）：130-134.

［8］张宇焜，汪伟英，周江江.注水压力对低渗透储层渗流特征的影响［J］.岩性油气藏，2010，22（2）：120-122.

［9］傅春梅，唐海，邹一锋，等.应力敏感对苏里格致密低渗气井废弃压力及采收率的影响研究［J］.岩性油气藏，2009，21（4）：96-98.

［10］史英，颜菲，李小波，等.考虑应力敏感疏松砂岩气藏试井分析［J］.岩性油气藏，2009，21（3）：114-117.

［11］李传亮.岩石应力敏感指数与压缩系数之间的关系式［J］.岩性油气藏，2007，19（4）：95-98.

［12］李传亮，王双才，周涌沂.岩石压缩系数对油藏动态储量计算结果的影响［J］.大庆石油地质与开发，2004，23（6）：31-32.

［13］张绍槐.多分支井钻井完井技术新进展［J］.石油钻采工艺，2001，23（2）：1-3.

［14］迈克尔 R.钱伯斯.多分支井［M］.孙仁远，译.北京：石油工业出版社，2006：77-172.

［15］石晓兵，喻著成，陈平，等.侧钻水平井、分支井井眼轨迹设计与控制理论［M］.北京：石油工业出版社，2009：1-62.

［16］赵军，王淼，祁兴中，等.轮西地区奥陶系地应力方向及裂缝展布规律分析［J］.岩性油气藏，2010，22（3）：95-99.

Analysis of seepage-stress coupling field for lateral wells

WEI Chen-xing，LIAN Zhang-hua，DING Liang-liang，GUO Yan-ruo，HAN Tao
（State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation，Southwest Petroleum University， Chengdu 610500， China）

There is very strong fluid-solid coupling during seeping in porous media.Taking full account of fluid-solid coupling in the COMSOL software for multilateral wells,the distribution characteristics of coupling seepage and stress field are analyzed,and the dangerous section ofsidewall is recognized accordingtocalculatingthe value offail coefficient by the Coulomb criterion.Through calculating the minimum value of fail coefficient and the volume integration in which fail coefficient is less than-2.5 MPa,the impact of the build-up rate on sidewall failure is studied.The results showthat the changes ofporosityis verysmall obtained in the simple seepage field byusingunique compressibilityfactor,while the porosityand permeability of the coupling seepage field change remarkably in the vicinity of the bottom.Therefore,fluidsolid coupling seeping is a true reflection of underground seepage.In the stress field,both the maximum valve of Von Mises equivalent stress and the minimum valve of coefficients fail emerge in the side tracking point of the lower lateral,which means that the sidetrack windowis the dangerous section of sidewall.Finally,the conclusion of smallest range of rock failure drilling lower lateral with build-up rate of 15°/30m is obtained,which provides a theoretical basis for the designingand buildingofthe multilateral wells.

lateral wells；seepage field；stress field；fluid-solid coupling；numerical simulation；borehole stability

TE243

A

2011-04-02；

2011-05-26

国家自然科学基金项目“基于数值模拟的复杂地层地应力场反演研究”（编号：50774063）资助。

魏臣兴，1979年生，男，西南石油大学在读博士研究生，主要从事CAD/CAE/CFD、管柱力学、地应力及岩石力学方面的研究。

地址：（610500）四川省成都市新都区西南石油大学博士 2009级。 电话：（028）83032210。E-mail：weichenxing@163.com

练章华，1964年生，男，博士，教授，博士生导师，现从事CAD/CAE/CFD、管柱力学、地应力及岩石力学等方面的教学与科研工作。E-mail：cwctlzh@swpu.edu.cn

1673-8926（2011）04-0124-05

于惠宇）