一种改进的K均值聚类算法
2011-01-12孟佳娜邓俐伶于玉海唐品忠
孟佳娜,邓俐伶,于玉海,唐品忠
(大连民族学院理学院,辽宁大连 116605)
一种改进的K均值聚类算法
孟佳娜,邓俐伶,于玉海,唐品忠
(大连民族学院理学院,辽宁大连 116605)
针对传统K均值算法中采取的欧氏距离计算相似性的不足,提出一种新的相似性计算方法,并将这种方法与欧氏距离的度量方法进行了比较。在UCI基准数据集上的实验表明,该方法有更稳定的聚类结果,是一种比较有效的聚类度量方法。
聚类分析;K均值算法;相似性
聚类分析广泛应用于模式识别、图像处理、文本挖掘等领域,是非常重要的数据分析方法之一。目前已提出的聚类算法有很多,这些算法可以被分为基于划分的方法、基于层次的方法、基于密度的方法、基于网格的方法和基于模型的方法[1]。在聚类方法中,K均值算法是最著名和最常用的划分方法之一。K均值算法由于实现简单、收敛速度快,自出现以来,已经提出了许多改进的算法。文献[2]提出了一种关于K均值的局部搜索近似算法;文献[3]针对初始中心敏感提出了一种选取初始聚类中心的算法。本文针对传统K均值算法中计算相似性和选取初始中心点的不足,提出一种改进的算法。
1 传统的K均值聚类算法
K均值法具有经典的聚类思想,逻辑简明清晰。它的主要步骤如下:
步骤1对给定的m×n矩阵X,给出k个n维向量作为初始中心点。
步骤2比较数据集当中样本点与各中心点间的距离,将各点划分到与其距离最近的类中,形成初始分类。
步骤3计算步骤2所形成的类的中心,使每类中心点得以更新。
步骤4重复步骤2和3,直到中心点不再移动,各类所包含的样本点也不再改变为止。
2 基于新的相似性度量方法的K均值聚类算法
聚类分析中数据结构可分为原始数据矩阵和距离矩阵。本文所讨论的方法采用原始数据矩阵。原始数据矩阵X为

式中,xij(i=1,…,m;j=1,…,n)为第i个样本的第j个属性的观测数据,第i个样本为矩阵X的第i行所描述。在进行聚类分析时,通过对原始数据矩阵进行相应操作来刻画样本之间的相似性。
本文所提出的K均值算法的改进主要体现在初始中心点的选取和相似性度量两个方面,下面介绍具体的改进方法。
2.1 初始中心点的选取
初始中心点的选择在K均值算法中非常重要,为了使各类具有一定的区分度,通常寻找散布较大的点作为初始中心点。在传统的算法中主要是随机选取初始中心点或是以前K个样本作为初始中心点,在本文的研究中,将按照如下方法来选取中心点:
(1)输入原始数据矩阵。
(2)计算原始数据各维的最大值与最小值,保存为maxj与minj,表示第j维上数值的最大值与最小值。
(3)利用公式

计算得到第l类的中心点在第j维上的值,该值始终在开区间(minj,maxj)内,且各中心点之间比较分散。
2.2 数据对象之间的相似性度量
对于聚类问题,一个算法产生的簇集可能有许多性质,所以说一个聚类问题中相似性度量[4]的选择是非常重要的。在传统的K均值算法中,将每个样本看成是高维空间中的一个点,进而定义点与点之间的距离,距离越大说明样本之间的相似性越小,距离越小说明样本间的相似性越大,这样得到的聚类结果是一些体积相近的球体。本文在传统的分组规则上进行改进,用曼哈顿距离来定义样本的属性之间的相似性,再将样本与样本之间的相似性用各个属性的曼哈顿距离来刻画。两个样本xa,xb之间的相似性可定义为

两个样本间的相似系数等于n个属性间相似系数之和,每对属性间的相似系数等于每对属性曼哈顿距离加1的倒数。式(2)把两个对象间每个属性的相似系数都映射到(0,1]区间,在每个属性的贡献相同的假设下,有更好的可解释性,而对于欧氏距离的度量方法,则会出现某个属性的影响远远大于其他属性甚至其他所有属性之和的现象,从而降低了其他属性在相似性度量中的作用,影响了样本类别的划分,对最终的聚类效果产生一定的影响。
3 实验结果及分析
本文实验中选择MyEclipse作为开发工具,使用java语言对算法进行实现。
3.1 聚类效果的评价
评价一项工作的结果,首先要找出评价的标准,进而根据标准确定评价指标,利用定量化的方法来实现科学的评价。本文中所用的评价标准基于准确率、召回率与F值[5]。对数据集中每个人工标注的主题为Pl。假设在聚类算法形成的类层次结构中存在一个与之对应的簇Cl。为了发现Cl,遍历聚类结果C={C1,C2,…,Ck},计算准确率、召回率和F值,从中挑选最优指标值及其对应的簇,以该最优的指标值来判定Pl的质量。对于任何人工主题Pl和聚类簇Cl:

3.2 实验结果
从UCI[6]数据集上选取4个数据集Iris,Wine,Soybean(small),Vehicle进行聚类分析。UCI数据集是一个专门用于测试机器学习、数据挖掘算法的公共数据集。本文对4个数据集进行了标准化和未标准化的对比实验,图1列出了本文算法未经标准化处理的实验结果。
从上述实验结果可以看出,改进算法对数据集Wine和Soybean聚类后值有大幅的提高,提高了20%左右。而另外两个数据集Iris,Vehicle则有所降低。Wine数据集有178个数据,分成3类,每个数据项有13个属性,各个属性的取值范围差距较大。Alcohol(属性1),Flavanoids(属性8),Color_intensity(属性11)这3个属性对分类最为重要,它们的取值范围分别为:(0.34~5.08),(1.28~13),(11.03~14.83),而对分类贡献不大的属性Proline(属性13)的取值范围是(278~1 680),在采用欧式距离计算相似性时,属性Proline起到了绝对的作用,导致使用欧氏距离聚类时严重降低了效果,而使用本文提出的相似度量方法则明显地减弱Proline(属性13)的影响,提高了聚类的结果。数据集Soybean的分布与Wine相似。

图1 原始数据未标准化的实验结果
由于数据集Iris的两个重要属性1(sepal length),属性2(sepal width)的取值都较属性3 (petal length)和属性4(petal width)大或相当,所以在这个数据集上并没有体现出本文提出的度量方法的优势。数据集Vehicle的分布跟Iris相似,故聚类结果没有大的变化。图2列出了标准化后的实验结果。
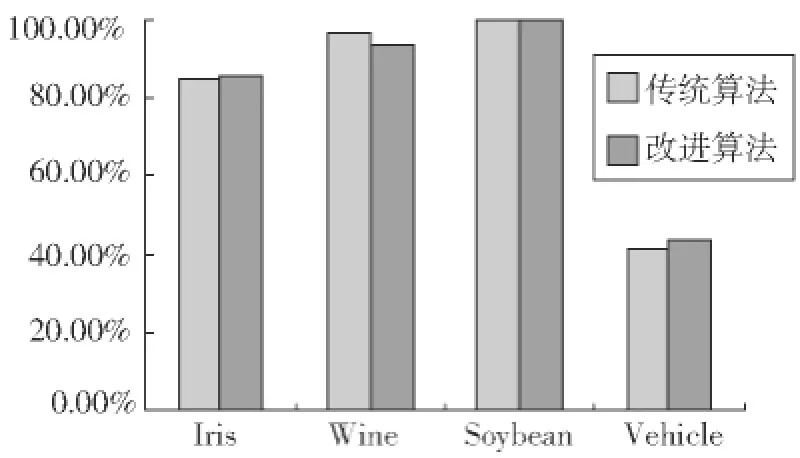
图2 原始数据标准化后的实验结果
从图2结果可以看出,在4个数据集上用改进算法都较原算法得到较好的聚类结果。
综合图1、图2及实验中得到数据可以得到如下结论:
(1)数据未标准化采用本文算法进行聚类,在数据集Wine,Soybean上的聚类效果好于原始的K均值算法,而在数据集Vehicle和Iris上,则效果有所下降。
(2)数据标准化和数据不标准化采用本文算法进行聚类,在大多数数据集上聚类效果波动不大,故改进算法相对于原算法有较为稳定的聚类结果。
4 结语
本文提出了一种新的相似性度量方法。由于它把每个属性的相似系数都映射到(0,1]之间,对于传统的聚类算法把对象中每个属性在聚类过程中的贡献看作是相同的假设,有更好的可解释性。在本文改进的K均值算法中,对于初始中心点的选取,只是尽量取各维数上的稀疏点,从根本上讲也是基于距离因素的选取。实际上,对于初始中心点,除了希望分布的尽量分散之外,还希望这些中心点具有一定的代表性,而本文改进的算法中并没有考虑到该因素,所以在初始中心点的选取上本文方法还有待进一步完善。
[1]HAN Jiawei,MICHELINE K.数据挖掘概念与技术[M].北京:机械工业出版社,2005.
[2]KANUNGO T,MOUNT D M.A local search approximation algorithm for k-means clustering[J].Computational Geometry,2004,28:89-112.
[3]BRADLEY P S,FAYYAD U M.Refining initial points for k-means clustering[C]//Proceedings of the 15th International Conference on Machine Learning,Morgan Kaufmann,San Francisco,CA,1998.
[4]史金成.基于相关性的数据流聚类及其应用研究[D].合肥:合肥工业大学,2007.
[5]张尧庭,方开泰.多元统计分析引论[M].北京:科学出版社,1982.
[6]http://archive.ics.uci.edu/ml/index.html.
An Improved K-Means Clustering Algorithm
MENG Jia-na,DENG Li-ling,YU Yu-hai,TANG Pin-zhong
(College of Science,Dalian Nationalities University,Dalian Liaoning 116605,China)
According to the disadvantages of calculating similarity based on traditional Euclidean distance of K-Means algorithm,a new similarity metrics method is presented.The given method is compared with the Euclidean distance of the K-Means clustering algorithm.The experiments based on UCI benchmark data sets showed that the method has more stable clustering results,and is an effective clustering metrics method.
cluster analysis;K-Means;similarity
TP18
A
1009-315X(2011)03-0274-03
2010-12-17;最后
2011-01-14
中央高校基本科研业务专项资金资助项目(DC10040118);大连民族学院教学改革项目(Y-09-2009-03)。
孟佳娜(1972-),女,吉林四平人,副教授,主要从事数据挖掘、自然语言处理研究。
(责任编辑 邹永红)
