显微镜放大照像识别微小长度

纠智先，赵 斌，徐滔滔

(武汉工业学院数理科学系，湖北武汉，430023)

在多种测量物体微小长度的方法中，利用光学显微镜是传统方法之一，它利用几何光学放大成像原理将微小物体充分放大，可以测量肉眼看不到的物质，在生物学和医学中被广泛使用［1-2］。但是一般情况下，利用测微目镜作为显微镜的标尺，其精度只有10μm，这远远不能满足实际需要。而能测量更精细长度的显微镜价格尤为昂贵，不适用普通大学物理实验室。同时，现已存在的各种数码显微镜可用来更好的拍摄和保存图像，但对测量方面没有过多考虑［3-5］。因此，如何能在通用实验工具基础上进行改进和创新，从而提高测量精度。本文主要介绍的实验方法利用显微镜将物体待测量进行充分清晰放大，再由数码相机拍照后将图像输入计算机内，利用画图工具可将图像的像素无损失的再次放大，实现物体待测量的二次放大，进而从像素点数来确定长度;其中，采用一级光栅(600条/mm)作为测量标尺，其光栅常数为1.667μm。

1 实验装置与原理

1.1 实验装置

实验装置，分别由显微镜、数码相机、光栅标尺、计算机组成。此实验装置是利用大学物理实验室中易获取的仪器、器材进行组合，实现对微小物体长度的测量。其中，显微镜、光栅是大学物理实验中基础的实验仪器。而数码相机和计算机无论是在生活还是工作中都是广泛通用的。采用显微镜的目镜分辨率为10倍，物镜分辨率为100倍，对待测的物理量能实现充分放大。数码相机为佳能单反相机，分辨率为1500万像素，能拍摄高质量的图像。光栅(600条/mm)作为测量标尺，其光栅常数为1.667μm。将拍摄光栅标尺和物体待测量的照片输入到计算机中，通过画图工具打开，其图像分辨率质量不会发生变化，实现图像的无损打开。

1.2 实验原理、方法和技术

首先，通过显微镜的几何光学成像原理将微小物体充分放大，由此获得清晰的像;然后，再利用数码相机对其拍照，获取高质量具有高分辨率的图像;最后，将获得的图像输入计算机，利用画图工具进行处理，最终得到物体待测量的长度。

选用显微镜的物镜放大倍率为100倍，通过无接触式充分放大测量物体。将数码相机通过固定装置稳固，从而拍摄最佳效果照片。

在实验中，选用光栅(600条/mm)，每相邻刻痕之间的长度即光栅常数作为实验数据标尺，光栅常数为1.667μm。

将拍摄的图像利用计算机中画图工具打开，可以获得标尺每单位所占的像素点数和物体待测量所占的像素点数，从而将后者与前者相比较，由此得到待测物体的长度。

该实验装置由数码相机拍摄实现样品的进一步放大，通过得到标尺和待测样品所占的像素点数，实现再次将样品充分放大的效果。同时，利用更有效的标尺(光栅)进行数据测量，进而实现对微小物体长度的精确测量。

2 实验数据分析

利用上述实验装置对头发丝的直径进行测量。通过显微镜放大将物体待测量和光栅标尺分别充分放大，拍摄图像。选用显微镜的物镜放大倍率为100，目镜放大倍率为10。将图像输入计算机中，使用画图工具分别打开拍摄图像。下面介绍实验数据分析及其误差分析。

头发丝直径的计算公式如下：

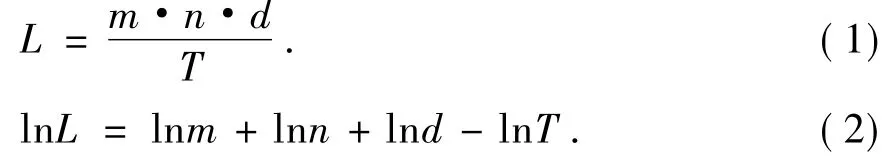
其中，L代表物体待测量的实际尺寸(mm);m为所拍摄的图像中，物体待测量所占的像素点数;n为图像中光栅条数;d为光栅常数，即1/600 mm;T为图像中n条光栅所占的总像素点数。

则头发丝直径的相对不确定度EL为［6］：

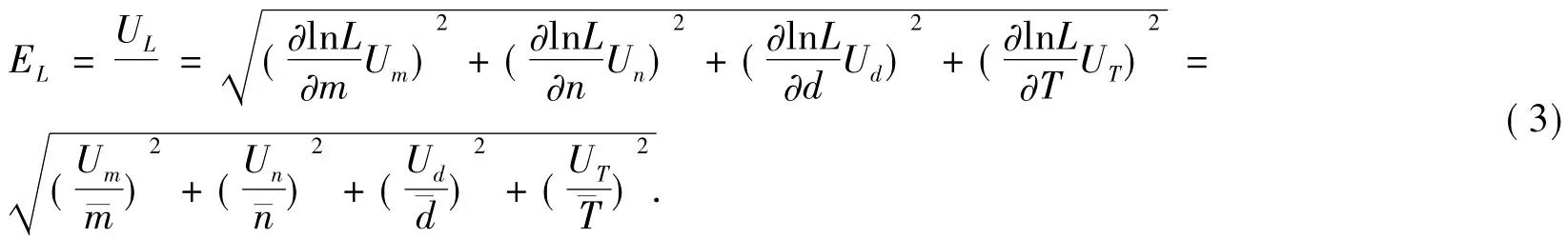
其中，Ux为不同变量的不确定度：

j为变量的总测量次数。

头发丝直径的不确定度UL为：

由于一级光栅的制作误差很小，即Ud在10-5毫米级，因此在计算过程中这一项可忽略不记。

从获取的光栅图像(如图1所示)中，由多次测量求平均可获得n条光栅所占的总像素点数，如表1所示。

表1 n条光栅所占的总像素点数

则光栅常数所占像素点数为3860.2/96.000=40.210。在图像中可分辨出96条光栅常数，估算出条数的误差在0.001条，因此在数据处理中，这一项也可忽略。

从获取的头发丝图像(如图2所示)中，由多次测量求平均获得的头发丝直径所占的像素点数，如表2所示。

表2 头发丝直径所占的像素点数

测量的标尺精确度为(即一个像素点所占的长度)为1/(600 ×40.210)=41.449 nm;计算得到的头发丝直径为¯L=84.35 μm，头发丝直径的相对误差E=0.19%;头发丝直径的不确定度 UL=0.16 μm;头发丝直径结果表达式为L=84.35±0.16(μm)。

该系统在实际操作过程中存在一定的视差和像差，由于头发丝质量因素导致其分布具有一定的不均匀性，同时还存在仪器误差、读数误差、工作台振动及环境干扰等。

本实验装置是利用放大原理对微小长度进行测量，精度高，并且原理简单，所用到的器材容易获得，具有很高的可行性，特色和创新点如下。

使用的实验仪器均易获取。

利用一级光栅(600条/mm)作为标尺，即每单位1.667 μm，比一般的测微目镜(每单位10 μm)更精细。

本作品分辨率可达0.04 μm，而光学显微镜的分辨率最高达0.1微米级。

利用数码相机对显微镜下显示的像进行拍摄，再利用计算机中的画图工具进行处理，将图像二次充分放大，可方便读数和计数，从而得到最终结果。比一般在显微镜下读数更方便省力，不易出错。

具有实时拍摄图像，并能获取具有高质量高分辨率的图像，同时和市场上的数码显微镜或者万能显微镜相比，造价要低更多。

综上所述，本实验装置具有无接触、分辨率高、操作简单省力、造价低等优点。

3 结论

采用显微镜将物体待测量及标尺充分放大，通过数码相机将所呈现的清晰的像拍摄下来，利用画图板工具对图像进行处理，实时得到物体待测量的准确读数，避免了在显微镜下费力的计数和计算等工作量。此实验装置适用范围广，各种微小物体长度的测量、无接触式测量、能利用显微镜观察的样品均能通过此方法进行测量。

大学物理实验室中一般都具备显微镜、光栅、数码相机、计算机等仪器物品，如此组合及操作能实现高精度的(放大长度测量)比现有的数码显微镜等仪器具有更多的实用性，便于推广。

［1］ 常青.万能工具显微镜纵向示值误差的影响因素及解决方法［J］.中国计量，2010(8)：99-100.

［2］ 吴大椿.用数码相机直接拍摄显微图像的应用技术［J］.湖北植保，2010(1)：53-54.

［3］ 曹西，南战推，贺铭，等.用家用数码照相机直接经显微镜目镜摄取高质量的数码图像［J］.生物学通报，2007，42(12)：49-50.

［4］ 李占坚.数码照相与计算机技术在台式金相显微镜上的应用［J］.装备制造技术，2010(6)：177-178.

［5］ 胡玉华，胡玉芝，陈守清.如何提高显微镜的分辨率［J］.品牌与标准化，2010(2)：48.

［6］ 徐滔滔.大学物理实验教程［M］.北京：科学出版社，2008：4-25.