基于遗传算法的小椭圆型储油罐的罐容表标定

王防修，周 康

(武汉工业学院数理科学系，湖北武汉430023)

通常加油站都有若干个储存燃油的地下储油罐，并且一般都有与之配套的“油位计量管理系统”，采用流量计和油位计来测量进/出油量与罐内油位高度等数据，通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算，以得到罐内油位高度和储油量的变化情况。

然而，许多储油罐在使用一段时间后，由于地基变形等原因，使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位)，从而导致罐容表发生改变。因此，如果能用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题，则可以实现储油罐的动态标定［1］。

要对一个变位的油罐实现准确标定不是一件容易的事情，即使是对如图1所示的变位小椭圆型储油罐的标定也是如此。许多人在标定的过程中用到所谓拟合［2］的方法，想通过该方法降低标定的误差。事实上，这种方法只适用事后分析，它对于通过油高来预测油量是没有任何帮助的。如果能够事先对倾斜角度的准确性进行合理修正，则对小椭圆型储油罐的标定才真正具有意义。本文借助小椭圆型储油罐所提供的实测数据［3］，通过相对误差的降低来说明这种修正的合理性。

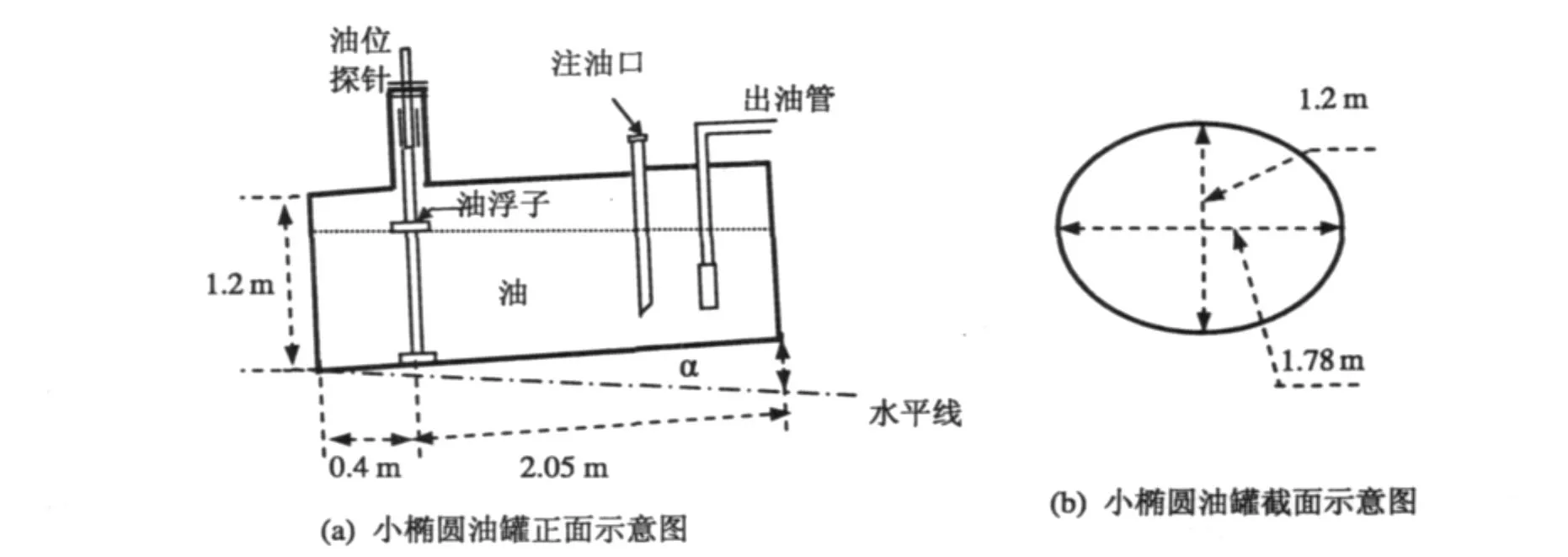
图1 小椭圆型油罐形状及尺寸示意图

1 小椭圆型储油罐的罐容表标定

1.1 小椭圆型油罐正常体位的标定

小椭圆型油罐正常体位(无变位)的不同油位高度与储油量的计算模型［4］是：

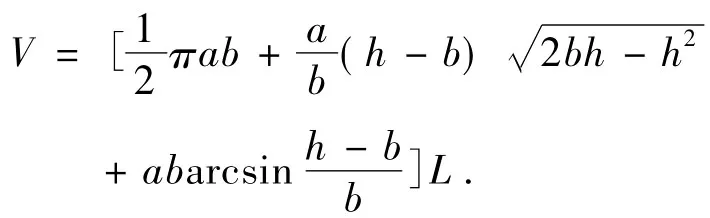
其中a，b，L分别为罐体截面椭圆的长半轴、短半轴和罐体长度，h为罐内的油位高度。通过代入几何参数计算得到如表1所示结果。

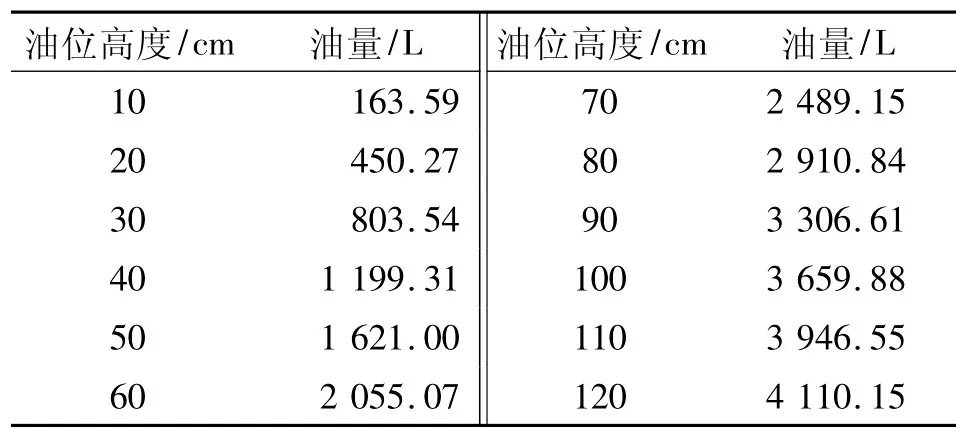
表1 正常情况下小椭圆罐的罐容表部分结果

1.2 小椭圆型油罐纵向倾斜变位后的标定

当油罐发生纵向倾斜时，如图2所示。罐体油量的体积随油位高度呈非线性变化，于是我们运用分段模式，使非线性转换为局部线性化。再根据各自的约束条件建立相应的数学模型。

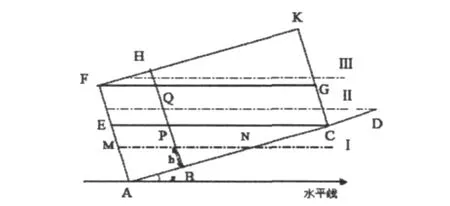
图2 纵向变位倾斜椭平顶截面示意图

已知：l=AB=0.4m，s=BC=2.05m，2b=AF=1.2m.

定义：h表示测得的油位高度，MN表示罐体油量高度的水平虚线，m表示对应椭圆底部深度，即m=AM，n表示上翘一端油面相对于罐底的高度，a表示小椭圆油罐横截面椭圆的半长轴，b表示小椭圆油罐横截面椭圆的半短轴。

实际储油罐仅纵向倾斜变位时，油量与油位高度、纵向倾斜角度α=4.10时的数学模型是：

当h≤PB时，

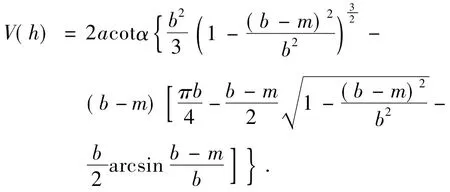
当PB＜h≤QB时，

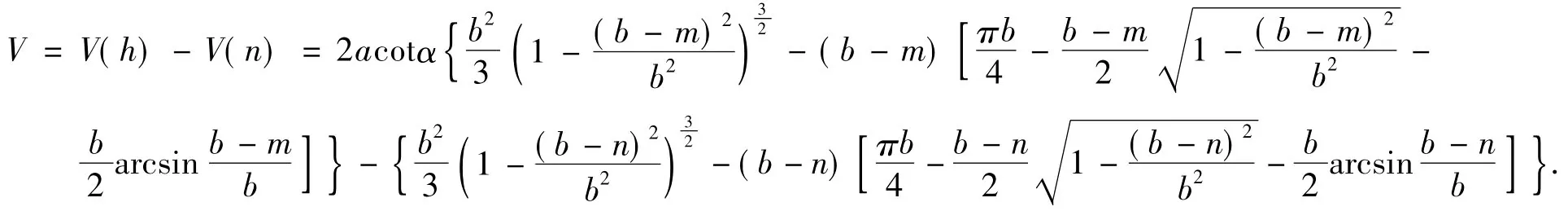
当h＞QB时，

将变位参数代入模型，计算出如表2所列的罐容表标定值。

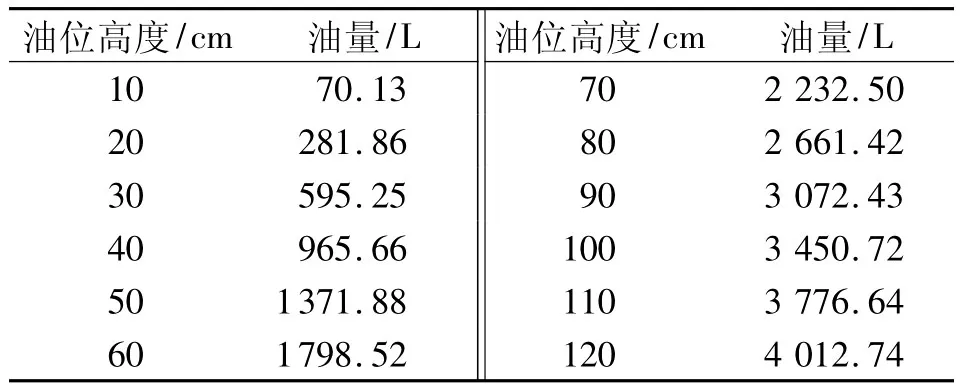
表2 小椭圆罐的α=4.10时的罐容表的部分结果

1.3 正常标定与变位标定的比较

与正常的标定值进行比较，对于纵向倾斜变位的影响明显，最大误差在257 L以上，平均误差达到190L以上，平均相对误差达30%以上。

2 遗传算法在小椭圆型储油罐的罐容表标定中的应用

2.1 误差分析

当将α=4.10与油位高度代入变位后的求油量模型中，得到如表3所示的部分数据。

从表3可以明显看出，油量的实测值与理论计算值之间的相对误差［5］还是相当大的。考虑到实际测量过程中存在测量误差，为此模型需要修正这方面的误差。由计算出的数据和实际测量的数据可得到平均相对误差¯e大于5%，但经分析会发现体积的实际值V和理论值Vm的绝对误差是很大的，在45—100 L内变动。存在几个影响模型的准确性的因素，分别为纵向倾斜角度α，油位高度h和油的体积V，现在主要考虑油位高度h和油的体积V准确的情况下，纵向倾斜角度α对模型准确性的影响。

表3 小椭圆罐的α=4.10时的罐容表的实测与模型计算的部分结果

2.2 用遗传算法［6］求倾斜角度α的最优值

2.2.1 用遗传算法求最优的倾斜角α

为了搜索到最优的α，需要将上述的变位油量模型变为V(h，α)，从而在油高相同的情况下，由不同的α可以计算出不同的油量。要找到最佳的α，其数学表达式可以表示如下。

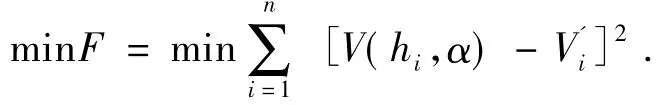
其中V(hi，α)表示油位高度为hi时用模型计算出的油量，表示第i时刻所测的实际油量，n代表实验数据个数。

根据实际情况，可以先将 α的范围锁定在［0.1，10.0］，如果最终的最优值在 0.1 或 10.0 附近，我们可以进一步修改α的范围。

为了使计算的结果精确到小数点后六位数，编码的二进制串至少需要22位。如果str1是一个22位的原色体，则首先将其转化为相应的十进制数x’，然后由译码过程即可以得到相应的角度α。

2.2.2 遗传算法的计算结果

通过执行遗传算法的计算机程序后，在区间［0.1，10.0］搜 索 到 最 优 的 染 色 体 编 码 为0111000011110011100001，经过译码得到最优的倾斜角α=5.382627°。将该倾斜角代入倾斜变位的标定模型中，可以得到如表4所示的结果。

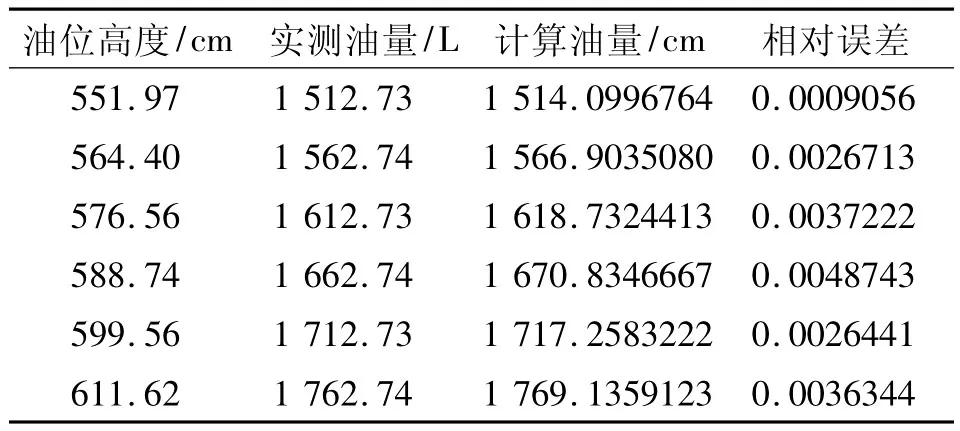
表4 小椭圆罐的α=5.382632°时的罐容表的实测与模型计算的部分结果

将表3与表4的结果进行比较，可以发现表4中计算数据与实测数据的相对误差已经非常小了。因此，我们认为α=4.1°不是非常准确的，可以将其修订为 α =5.382632°

2.2.3 与用粒子群算法计算的结果比较

用粒子群算法计算的倾斜角α =5.38261°，将该倾斜角代入倾斜变位的标定模型中，可以得到如表5所示的结果。

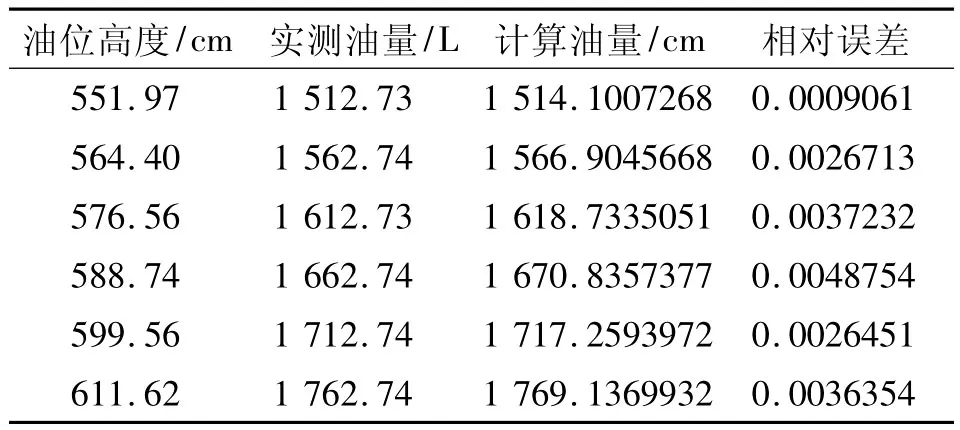
表5 小椭圆罐的α=5.38261°时的罐容表的实测与模型计算的部分结果

对表4与表5的结果进行比较，可以发现用遗传算法计算的结果更加准确。这是由于粒子群算法比遗传算法容易陷入局部最优。

3 小椭圆型油罐纵向倾斜变位(倾斜角度修正)后的标定

通过前面的数据分析，我们已经知道将α =4.1°修订为 α =5.382627°可以得到更好的标定效果。因此，将α=5.382627°和油位高度代入标定模型中得到的标定值如表6所示。

对表2和表6的结果进行比较，可以标定的结果差别很大。α=5.382632°求得的体积函数与实际情况比较相符，从而我们有理由相信以上所建立的数学模型具有一定的可靠性。

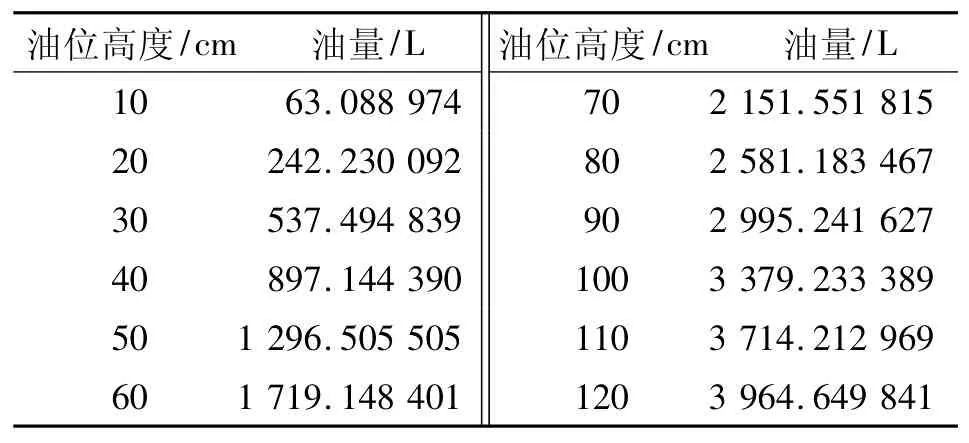
表6 小椭圆罐 α=5.382632°时的罐容表的部分结果

4 结束语

本模型属于单一变位情况，还有比这复杂得多的变位情况，需要对其进一步深入探讨。这里重在介绍用遗传算法搜索最优的倾斜角度。储油罐有一个特定的纵向倾斜变位，计算出油位高度与油量的函数关系式，通过几何关系分析和微分方程求解，逐步逼近储油罐有任意的变位参数时，得到油位高度与油量的一般关系，保证了模型的普遍适用性。

［1］ 葛动元，姚锡凡，李凯南.双目立体视觉系统的标定［J］.机械设计与制造，2010(6)：188-189.

［2］ 于光伟，赵玉刚.椭圆弧等误差直线拟合的算法研究与轨迹仿真［J］.山东理工大学学报，2010(1)：89-92.

［3］ 中国工业与应用数学学会.2010年全国大学生数学建模题目［DB/OL］.http：//www.mcm. edu. cn/upload _ cn/node/70/rd4LEPmmd1095c70a7fb9d0898a08495837d8c93.rar，2010-09-17/2010-10-14.

［4］ 同济大学应用数学系.高等数学［M］.北京：高等教育出版社，1993：233-288.

［5］ 刘俊杰，张文阁.光阻法液体颗粒计数器粒径档设定相对误差的检定方法探讨［J］.中国粉体工业，2010(1)：14-16，21.

［6］ 李华昌，谢淑兰，易忠胜.遗传算法的原理与应用［J］.矿冶，2005(1)：87-90.