* 关于整数线性规划全部最优解的一个注记
2011-01-11高太平刘桂枝刘宏英
高太平,刘桂枝,刘宏英
(1.山西大学计算机与信息技术学院,山西太原 030006;2.计算智能与中文信息处理省部共建教育部重点实验室,山西太原 030006;3.山西大同大学物理与电子科学学院,山西大同 037009;4.山西大同大学数学与计算机科学学院,山西大同 037009)
*关于整数线性规划全部最优解的一个注记
高太平1,2,刘桂枝1,3,刘宏英1,4
(1.山西大学计算机与信息技术学院,山西太原 030006;2.计算智能与中文信息处理省部共建教育部重点实验室,山西太原 030006;3.山西大同大学物理与电子科学学院,山西大同 037009;4.山西大同大学数学与计算机科学学院,山西大同 037009)
研究在整数线性规划基最优解已经求出且不唯一的条件下,如何求整数线性规划的全部最优解问题.当整数线性规划具有两个基最优解时,文章给出其全部最优解的个数公式及求全部最优解的一个有效算法.
整数线性规划;单纯形法;最优解;算法
0 引言
整数线性规划在许多研究和应用领域都起着重要作用,如Job-shop调度问题[1]、物流最优调度问题[2-3]、指派问题[4-5]、装载问题[6]等.现实生活中的许多决策问题,往往可以归结成整数线性规划问题.因此,整数线性规划求解问题引起了数学科学、管理科学、决策科学、系统科学等领域专家学者的广泛兴趣.然而由于整数线性规划问题固有的复杂性和难解性,使其求解不像线性规划那么容易.人们已经证明整数线性规划的求解问题是NP-难的[7].目前实用可行的方法如分支定界法、割平面法等在大多数情况下只能求出整数线性规划的一个或很少几个整数最优解.当整数线性规划的最优解不唯一时,如何求其全部最优解或更多最优解,至今仍没有一个通用而有效的算法.鉴于此,本文主要针对整数线性规划具有两个基最优解的情况进行研究,给出了其全部最优解的个数公式以及求全部最优解的一个有效算法.
1 预备知识
1.1 基本概念
设线性规划的标准型为
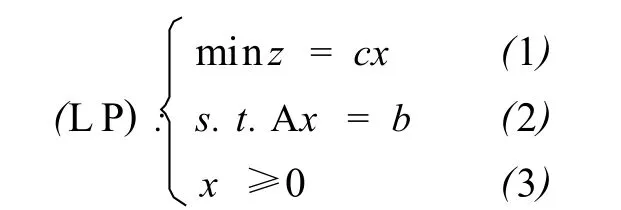
其中,x,c∈Rn,b∈Rm,A为m×n矩阵,A的秩为m(m<n).满足约束条件(2)、(3)式的解X=(x1,x2,…,xn)T称为线性规划问题(LP)的可行解,全体可行解组成的集合称为(LP)的可行域,其中使目标函数达到最小值的可行解称为(LP)的最优解.若B=(Aj1,A j2,…,A jm)是矩阵A中m×m阶非奇异子阵(|B|≠0),则称B是线性规划(LP)的一个基,xj1,xj2,…,xjm称为关于基B的基变量,其余变量称为关于基B的非基变量.非基变量全取0时,(2)式的解称为(LP)的基解,满足非负条件(3)的基解称为(LP)的基可行解,使目标函数取得最小值的基可行解称为基最优解.
设K是n维欧氏空间的一个点集,若任意两点X(1)∈K,X(2)∈K的连线上的所有点λX(1)+(1-λ)X(2)∈K(0≤λ≤1),则称K为凸集.
文中未定义的记号和术语请参见文献[8].
1.2 几个引理
为了讨论整数线性规划的全部最优解,我们需要下面几个定理.
引理1[8]若线性规划问题存在可行解,则其可行域D={X|A X=b,X≥0}是凸集.
引理2[8]X为(LP)的基可行解的充分必要条件为:X为(LP)的可行域D的顶点.
引理3[8]若(LP)的可行域D有界,则(LP)的目标函数一定在D的某些顶点上达到最优.
引理4[8]若(LP)的可行域有界,且全部基最优解为X(1),X(2),…,X(k),则(LP)的任一最优解可表示为

引理5[9]设B=(A j1,Aj2,…,Ajm)是(LP)的一个最优基,对应的基最优解为X.若存在k∈{1,2,…n}{j1,j2,…,jm},使得判别数σk=cBB-1Ak-ck=0,则取xk为进基变量进行换基迭代,可得另一基最优解 ̄X.
2 具有两个基最优解的整数线性规划全部最优解的个数
设整数线性规划的标准型为


①取rl=0时,由归纳假设2)知,λ有f(k1,k2,…,kl-1)-2种取法;
②取ri=0,i=1,2,…,l-1时,λ有kl种取法;
③取r1r2…rl-1rl≠0时,对每个rl∈{1,2,…,kl},λ有f(k1,k2,…,kl-1)-2种取法.所以,在这种情况下,λ共有(f(k1,k2,…,kl-1)-2)kl种取法.
综合①-③,我们有
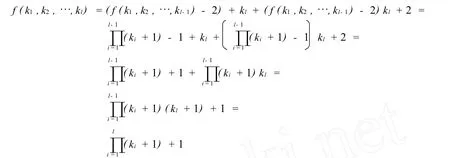
命题得证.
3 具有两个基最优解的(IL P)全部最优解的求解算法
设(ILP)具有两个基最优解X(1),X(2),由上面的讨论,结合定理1和定理2,我们给出求解(ILP)的全部整数最优解的算法如下:

4 实例
求解下列(ILP1)的全部最优解

解 利用单纯形法,可得到(ILP1)的最优单纯形表如下(见表1,P8):
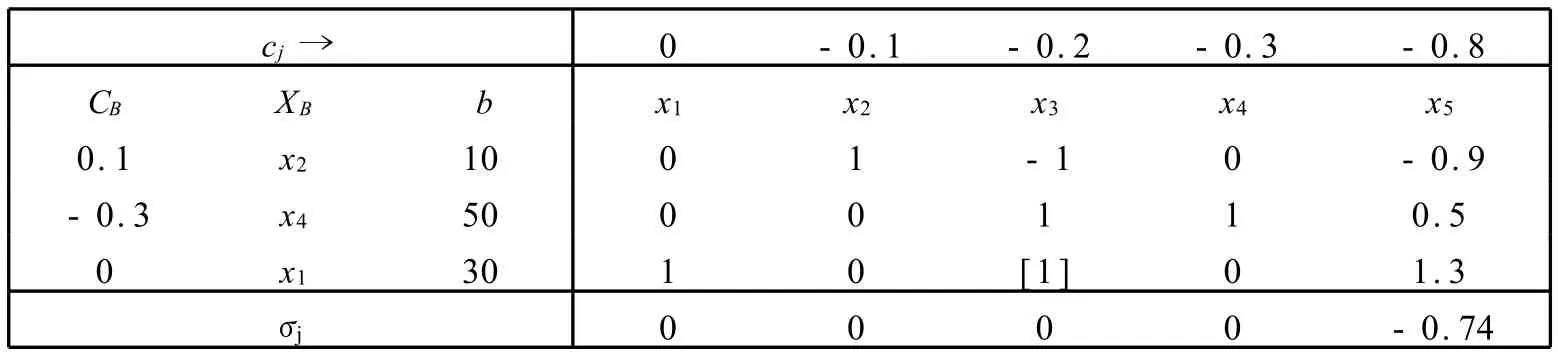
表1 (ILP1)的最优单纯形表Table 1 Optimal Simple Table of(ILP1)
根据最优单纯形表1,我们可求得第一个基最优解为X(1)=(30,10,0,50,0).由于表1中非基变量x3对应的判别数σ3也为0,所以由引理5可知,(ILP1)还存在另外一个基最优解.这时,只要取x3为进基变量,x1为离基变量,再做一次换基迭代,便可以求出另一个基最优解为X(2)=(0,40,30,20,0).此时d=30=21×31×51,所以原问题(ILP)的全部整数最优解个数为f(1,1,1)=(1+1)×(1+1)×(1+1)+1=9.
下面求除X(1),X(2)以外的其余9-2=7个最优解.为此,依次取
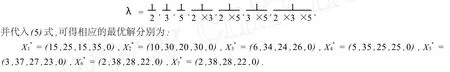
5 结束语
本文基于单纯形法,在整数线性规划恰有两个基最优解的条件下,给出了求整数线性规划全部最优解的一种有效算法.从而可为此类实际问题提供更多的最优方案,使得决策者在某些最优方案因一些突发事件不能使用时,可更多地选择其它最优方案.尽管算法是在已知两个基最优解的条件下给出的,但是在整数线性规划具有两个以上已知(基)最优解的情况下(不管得到这些最优解是基于单纯形法或者分枝定界法,还是其他方法),欲求更多其它最优解时,该算法也是有效的.这时,尽管我们不一定能求出全部最优解,但只要从这些已知的最优解中任意选取两个,按照上述算法便可求出更多的最优解.从实用角度来讲,这已经足够了.从理论分析来看,当整数线性规划具有三个或更多基最优解时,求其全部最优解将变得异常复杂,甚至是不可能的.因此,本文给出的算法具有一定的理论意义和实用价值.
[1] 李琳,霍佳震.钢管生产计划中的多目标柔性Job-shop调度问题[J].系统工程理论与实践,2009,29(8):117-126.
[2] 刘苏庆,曹成铉,郑辉文.集装箱多式联运中运货排程问题的建模研究[J].科学技术与工程,2010,10(9):2247-2250.
[3] 陈锋,邢文训.超尺寸物品装箱问题[J].运筹学学报,2002,6(1):85-90.
[4] Bihr R A.A Conceptual Solution to the Aircraft Gate Assignment Problem Using 0-1 Linear Programming[J].Computers and Industry Engineering,1990,19(3):280-284.
[5] Aissi Hassene,Bazgan Cristina,Vanderpooten Daniel.Complexity of the min-max and min-max Regret Assignment Problem s[J].Operations Research Letters,2005,33:634-640.
[6] 唐国春.现代物流技术中装卸工问题的拟多项式时间可解情况[J].运筹与管理,2005,14(4):15-18.
[7] Papadimitriou C H,Steiglitz K.Combinato rial Optimization Algorithm s and Complexity[M].Printice-Hall Inc,1982.
[8] 魏国华,王芬.线性规划[M].北京:高等教育出版社,1990.
[9] 陈开周.最优化计算方法[M].陕西:西北电讯工程学院出版社,1986.
A Note on All Optimal Solutions of Integer Linear Programming
GAO Tai-ping1,2,L IU Gui-zhi1,3,LIU Hong-ying1,4
(1.School of Computer&Information Technology,Shanxi University,Taiyuan030006,China;2.Key Lab of the Com putation Intelligence and Chinese Information Processing Province Department Altogether Constructs the M inistry of Education,Taiyuan030006,China;3.School of Physics and Electronic Science,Shanxi Datong University,Datong037009,China;4.School of Mathematics and Computer Science,Shanxi Datong University,Datong037009,China)
How to get all optimal solutions of ILP(integer linear programming)was studied if its basic optimal solution is not unique.When the two basics solutions of ILP is gotten,the formula on the number of all optimal solutions and the effective algorithm getting all the optimal solutions for ILP were got.
integer linear programming;simple method;optimal solution;algorithm
O221
A
0253-2395(2011)01-0005-05*
2010-06-07;
2010-09-23
国家自然科学基金(60803034);山西省自然科学基金(2007011043)
高太平(1956-),男,教授,主要研究方向:组合优化、算法设计与分析.E-mail:tpgao@sxu.edu.cn
