＊ 冠状动脉系统的复杂动态与混沌控制

石艳香,刘桂荣,白定勇

(1.山西大学数学科学学院,山西太原 030006;2.广州大学数学与信息科学学院,广东广州 510006)

＊冠状动脉系统的复杂动态与混沌控制

石艳香1,2,刘桂荣1,白定勇2

(1.山西大学数学科学学院,山西太原 030006;2.广州大学数学与信息科学学院,广东广州 510006)

研究两类冠状动脉系统:N型与S型.利用Melnikov方法,得到两类系统在参数条件下产生Smale马蹄意义上的混沌的阀值.通过数值模拟,不仅可以证明理论分析的正确性,同时显示出理想的分支图形和更多新的复杂动力学行为.数值模拟包括相图、势能图、同宿分支曲线和分支图,通过这些较直观地反映出系统随周期激励外力强弱变化的动态特性、复杂性和非线性特征,揭示了系统的分支形式以及通向混沌运动的道路.最后对系统的混沌运动状态进行了有效的控制.

Melnikov方法;混沌;分支;混沌控制

混沌科学是20世纪人类三大科学成就之一,自上世纪60年代Lo renz系统被发现以来,已有许多新的混沌系统被相继提出[1-2],这些系统的提出,促使混沌理论研究不断深入,并为混沌在信息处理、保密通讯等工程技术领域内的应用提供了支持.

周期激励冠状动脉系统是一种典型的非线性振动系统,有着丰富的动力学行为.

(A)周期性激励N型血管的非线性数学模型为[3]

(B)周期性激励S型血管的非线性数学模型为[3]

本文针对系统(1)和系统(2)进行分析.研究表明,此二系统可能存在混沌运动.王树禾[4]给出了冠状动脉的方程模型及其混沌表现,利用Melnikov方法给出两类系统产生混沌的条件.Melnikov方法[5]是判定二维系统是否存在混沌现象的重要理论依据.张莉等[6]研究了Van der Pol-Duffing振子的混沌及其控制.褚衍东等[7]研究了Van der Pol-Duffing耦合系统的分岔与混沌控制.石艳香等[8]研究了一类Josephson系统的混沌及其控制.目前,各种文献中对冠状动脉系统的混沌控制研究尚少,作为控制科学当中一个重大课题,有必要对该系统的混沌控制做深入的研究.

对系统(1),ε=0时是Hamilton系统,其Hamilton量为

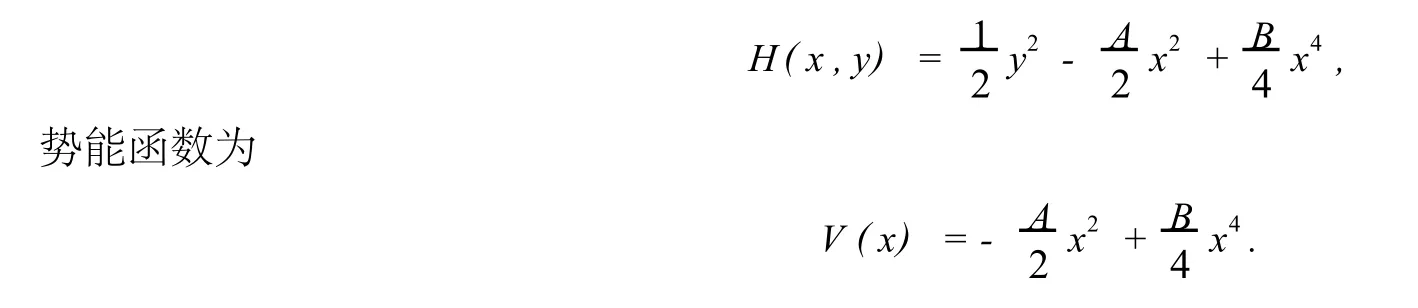
图1(a)和(b)分别给出了ε=0时系统(1)的相图和势能图,此时取A=B=1.图1(a)中,鞍点(0,0)通过两条同宿轨Γ±N连接自身.

图1 系统(1)的相图和势能图,这里ε=0,A=B=1Fig.1 Phase portrait and potential of the system(1)forε=0,A=B=1

当ε=0,F=D=1时系统(2)的相图和势能图与系统(1)相同,此时鞍点(0,0)通过两条同宿轨连接自身.

下面利用数值模拟为上面的理论分析提供依据,并且去寻求系统更复杂的动力学行为.

首先给出系统(1)的数值模拟.图2给出的是在(ω,r)平面上马蹄混沌的M elnikov起始曲线图,此时:δ=0.5,A=1,B=1.从图2结合(4)式可知:在曲线的下方鞍点的稳定流形和不稳定流形不发生横截相交,而在曲线的上方,上述行为发生,即鞍点的稳定流形和不稳定流形发生横截相交.也就是说,只有在曲线的上方才可能发生混沌.

图2 系统(1)在(ω,r)平面上的Smale马蹄混沌起始曲线图.在曲线的上方发生同宿分支的横截相交Fig.2 Homoclinic bifurcation curve for Smale chaos in the(ω,r)p lane.Transverse intersections of homoclinic orbits occur above the curve

下面对系统(1)进行数值模拟.选取系统参数:A=1,B=1,δ=0.5,ω=1,r1=0.01,r2=0.001,采用四阶变步长Runge-Kutta算法对系统(1)进行数值模拟,选取r为分支参数,得到系统在r∈(0,1)区间内的分支图,如图3(a)所示(P17).从图3(a)中可以看到倍周期分支和逆倍周期分支,混沌和周期窗口.为进一步清晰,图3(b)显示了0.3≤r≤0.5时放大的倍周期段;图3(c)和图3(d)分别显示的是0.4≤r≤0.65和0.55≤r≤0.8时放大的混沌窗口.从r=0开始并且随着r的逐渐增大系统(1)处于稳定的1周期状态,在r≈0.346 69时发生倍周期分支,即原先的1周期轨道变的不稳定,且产生了稳定的2周期轨道.随着r继续增大,系统陆续发生倍周期分支,且产生稳定的4周期轨道、8周期轨道、16周期轨道…,当r≈0.587 17时发生混沌,而通过(4)式得到的混沌的阀值是r=0.590 2,两者近乎相近,说明了理论分析与数值模拟的一致性.从图3(c)中发现有5周期窗口和3周期窗口的存在.图3(d)中显示出存在一个3周期窗口.当r≈0.829 66时系统混沌消失,开始产生逆倍周期分支,最终成为稳定的1周期轨道.图4(P17)(a)(b)(c)(d)显示的是r=0.1(周期-1轨道);r=0.355(周期-2轨道);r=0.8(混沌状态)和r=0.9(周期-1轨道)时的系统(1)的相图.可以看到系统从周期轨到混沌、再由混沌到周期轨的过程.

其次给出系统(2)的数值模拟.图5(P17)给出的是在(ω,r)平面上马蹄混沌的Melnikov起始曲线图,此时:δ=0.5,F=1,D=1,δ1=0.05,δ3=0.2.再结合(5)式知:曲线下方的鞍点的稳定流形和不稳定流形不发生横截相交,而曲线上方的鞍点的稳定流形和不稳定流形发生横截相交,即在曲线的上方可能发生混沌.

图3 (a)系统(1)以 r分支参数的分支图.(b)(c)(d)分别为图3(a)在(r,x)平面上的放大分支图Fig.3 (a)Bifurcation diagram of the system(1)in(r,x)plane.(b)(c)(d)Amplifed bifurcation diagrams of Fig.3(a)

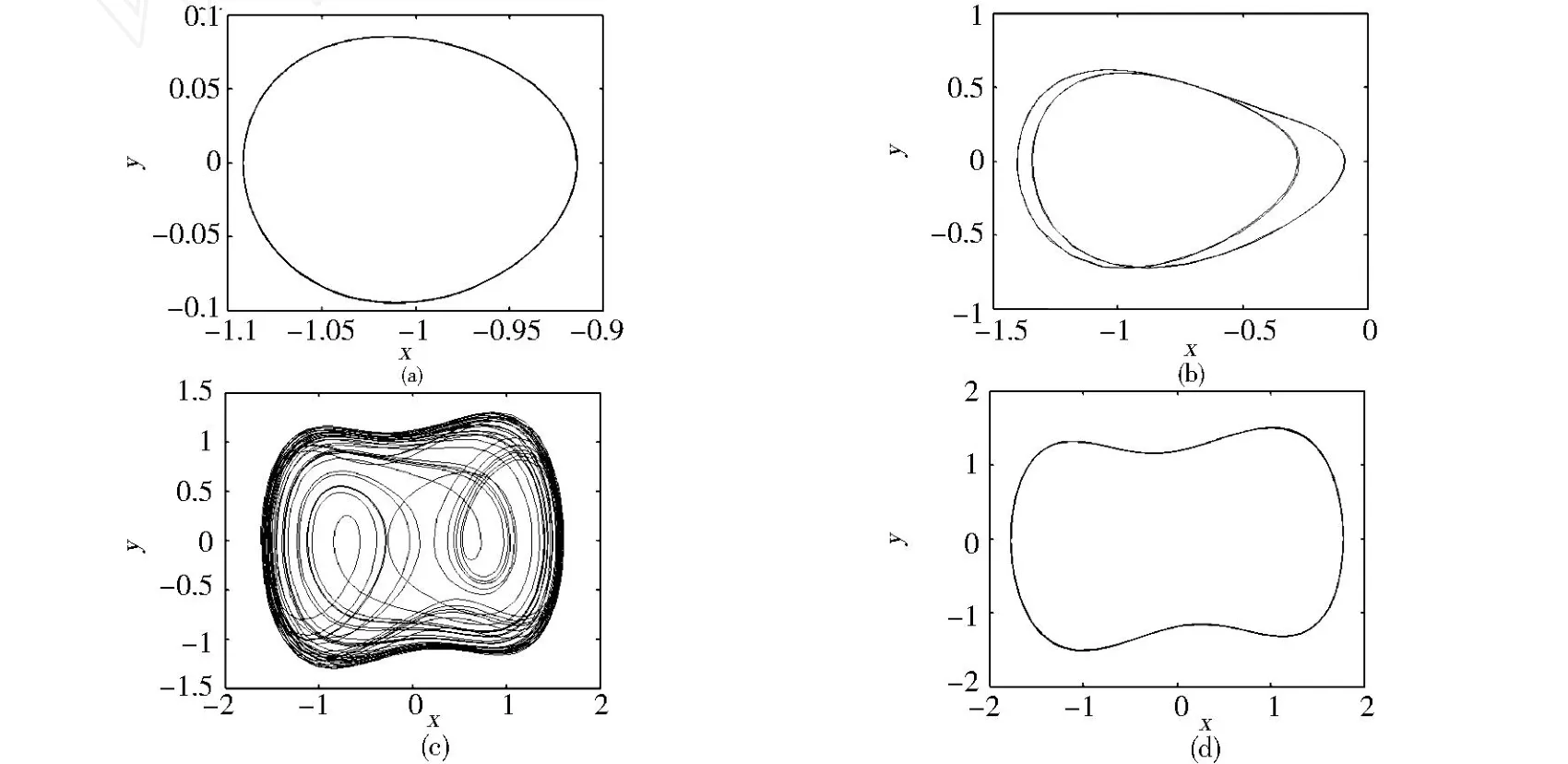
图4 系统(1)在不同分支变量 r下的相图Fig.4 Phase portraits of the system(1)

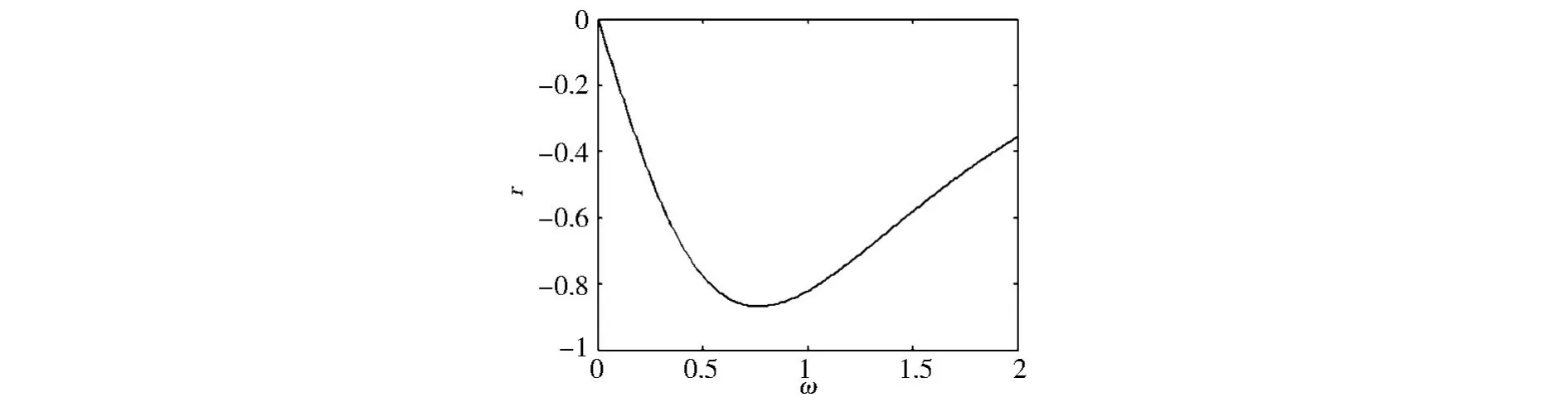
图5 系统(2)在(ω,r)平面上的Smale马蹄混沌起始曲线图.在曲线的上方发生同宿分支的横截相交Fig.5 Homoclinic bifurcation curve for Smale chaos in the(ω,r)p lane.Transverse intersections of homoclinic orbits occur above the curve

下面对系统(2)进行数值模拟.选取系统参数:F=1,D=1,δ=0.5,δ1=0.05,δ2=0.1,δ3=0.2,ω=1,r1=0.01,r2=0.001,图6(a)为外周期激振力的幅值r在(0.4,1.4)之间变化的分支图.从图中可以观测到倍周期分支、逆倍周期分支、混沌和周期窗口.图6(b)(c)(d)为图6(a)分别在r∈(0.55,0.8),r∈(0.78,0.88)和r∈(0.8,1.2)上的放大分支图.三幅图中都可以看到有倍周期分支和逆倍周期分支的存在,并且存在不同周期的周期窗口:(b)3周期窗口;(c)2周期窗口;(d)3、4、5、7周期窗口.图7(a)(b)(c)(d)分别显示的是r=0.68(周期-3轨道);r=0.82(周期-2轨道);r=0.98(周期-n轨道)和r=1.1(混沌状态)时的相图.

图6 (a)系统(2)在(r,x)平面的分支图.(b)(c)(d)分别为图6(a)在(r,x)平面上的放大分支图Fig.6 (a)Bifurcation diagram of the system(2)in(r,x)p lane.(b)(c)(d)Amplified bifurcation diagrams of Fig.6(a)

图7 系统(2)在不同分支变量 r下的相图Fig.7 Phase portraits of the system(2)

以上理论和数值研究结果表明,在某些参数下系统处于混沌状态.为了抑制和消除系统的混沌行为,要对系统的混沌进行控制.以下介绍两种方法来对混沌进行控制.

1)变量反馈控制

利用变量反馈控制方法对系统进行控制,该方法不仅能稳定原系统中的不稳定周期轨,而且能建立新的周期轨道.

在系统(1)中加入一个反馈变量K(K为可调节的反馈系数),得到控制后的方程

通过选取适当的K,便可抑制系统的混沌行为.图8(a)为系统(6)在反馈变量K∈(0,1)下的分支图,这里参数固定:A=1,B=1,δ=0.5,ω=1,r1=0.01,r2=0.001,r=0.8.从图8(a)可以看到带有2周期窗口和3周期窗口的混沌区域.当K≈0.593 19时,系统开始发生逆倍周期分支,即混沌消失,产生…、16周期轨道、8周期轨道、4周期轨道、2周期轨道,直到稳定的1周期轨道.以上的状态过程说明反馈变量K对系统原先的混沌状态产生了抑制作用:混沌消失,周期轨道产生.图8(b)(c)(d)给出了系统在不同反馈变量K受控下的相图:(b)K=0.2,周期-2轨道;(c)K=0.4,周期-3轨道;(d)K=0.8,周期-1轨道.从图8(b)(c)(d)可以进一步看出系统状态从混沌到周期轨道.

图8 (a)系统(6)对反馈变量 K∈(0,1)的分支图.(b)(c)(d)系统(6)在不同反馈变量 K下的相图Fig.8 (a)Bifurcation diagram of the system(6)in K∈(0,1).(b)(c)(d)Phase portraits for three values of K in Fig.8(a)

2)耦合反馈控制

用周期信号y(t)和系统(2)的输出结果x(t)进行耦合后作为控制信号f(t),即f(t)=L(x(t)-y(t)),其中L为控制信号的权重,用以调节控制信号的强度,于是可以得到系统(2)被控制后的方程为

图9(a)给出了系统(7)在L∈(0,1)下的分支图,这里参数固定:F=1,D=1,δ=0.5,δ1=0.05,δ2=0.1,δ3=0.2,ω=1,r1=0.01,r2=0.001,r=1.1.从图中可以看到带有2,3周期窗口和5周期窗口的混沌区域,系统从L=0开始时仍处于混沌状态.在L=0.410 82附近,系统发生逆倍周期分支,状态由原先的混沌态开始转化为周期状态.分支变量L对系统的混沌产生了抑制.图9(b)(c)(d)给出了系统在不同分支变量L下的相图:(b)L=0.01,混沌状态;(c)L=0.3,周期-3轨道;(d)L=0.8,周期-1轨道.通过图9可以很好的找到合适的控制参数.

图9 (a)系统(7)对分支变量L∈(0,1)的分支图.(b)(c)(d)系统(7)在不同分支变量L下的相图Fig.9 (a)Bifurcation diagram of the system(7)in L∈(0,1).(b)(c)(d)Phase portraits for three values of L in Fig.9(a)

[1] Chen G R,Ueta T.Yet Another Chaotic Attractor[J].Int J Bifurcation and Chaos,1999,9(7):1465-1466.

[2] Qi G Y,Chen G R,Du S Z,Chen ZQ,Yuan Z Z.Analysis of A New Chaotic System[J].Physic A,2005,352(2-4):295-308.

[3] 李继彬.混沌与Melnikov方法[M].重庆:重庆大学出版社,1989.

[4] 王树禾.微分方程模型与混沌[M].合肥:中国科学技术大学出版社,1999.

[5] 刘增荣.混沌的微扰判据[M].上海:上海科技教育出版社,1995.

[6] 张莉,俞建宁,李阳,等.Van der Pol-Duffing振子的混沌及控制[J].温州大学学报:自然科学版,2007,28:11-14.

[7] 褚衍东,李险峰,张建刚.Van der Pol-Duffing耦合系统的分岔与混沌控制[J].江南大学学学报:自然科学版,2007,6:119-123.

[8] 石艳香,白定勇,陶为俊.一类Josephson系统的混沌及其控制[J].河南师范大学学报:自然科学版,2010,5:8-12.

Complex Dynamics and Chaos Control in Coronary Artery System

SHI Yan-xiang1,2,LIU Gui-rong1,BA IDing-yong2
(1.School of Mathematica l Sciences,Shanxi University,Taiyuan030006,China;2.School of Mathematics and Information Sciences,Guangzhou University,Guangzhou510006,China)

N-type and S-type,two types of coronary artery system are investigated.Applying Melnikov method,the threshold conditions for the occurrence of Smale horse chaos of the two types are obtained respectively.By numerical simulation,not only the correctness of theoretical analysis is proven but also the ideal graphics and mo re new bifurcation of the comp lex dynamic behavior are show n.Numerical simulations,including phase diagram,potential diagram s,homoclinic bifurcation curve diagram s and bifurcation diagram s,are used to investigate the dynamic characteristics,the complexity and the nonlinear dynamics characteristic of the two system s,and to reveal bifurcation form s and the road leading to chaotic motion.Finally the chaotic states of motion are effectively controlled.

Melnikov method;chaos;bifurcation;chaos control

O322;O175

A

0253-2395(2011)01-0014-07＊

2010-08-05;

2010-11-09

数学天元青年基金(10826080);山西省青年科技研究基金(2009021001-1);广东省自然科学基金博士科研启

动项目(9451009101003172);广州市教育局市属高校科技项目(08C015);高校博士点资助课题(20061078002)

石艳香(1979-),女,山西阳泉人,讲师,在读博士,主要研究方向:微分方程理论及其应用.E-mail:hongyu1979321@163.com

book=20,ebook=167