基于Matlab的单闭环直流调速系统仿真实验设计

尚 丽，陈 杰

(苏州市职业大学 电子信息工程系, 江苏 苏州 215104)

调速系统的转速降落是由负载引起的转速偏差，引入转速闭环将使调速系统大大减少转速降落，从而大大降低系统的静差率，提高直流电动机调速控制系统的稳定性[1-3].另外，在转速单闭环调速系统中，当转速调节器(automatic speed regulator，ASR)采用比例(proportion，P)调节器时，该调速系统是有静差的;为了消除系统的静差，可用积分(integration，I)调节器或者比例积分(proportion integration,PI)调节器代替P调节器构成无静差转速单闭环直流调速系统.本文讨论的无静差转速单闭环直流调速系统采用PI调节器作为转速调节器.

近年来，随着计算机技术的发展，仿真技术逐步发展，现已形成完整的学科，渗透到各个领域，为应用系统的研究提供了强大的工具.目前，使用Matlab对控制系统进行计算机仿真的主要方法是以控制系统的传递函数为基础，使用Matlab的Simulink工具箱对其进行计算机仿真研究，而本文应用的是一种面向控制系统的电气原理结构图，使用电力系统工具箱(sim power systems)进行转速单闭环直流调速系统仿真的新方法.使用电力系统工具箱，用户不需要自己编程且不需推导系统的动态数学模型，只要从工具箱的元件库中复制所需的电气元件，按电气系统的结构进行连接即可[4-6].系统的建模过程接近实际系统的搭建过程，而且元件库中的电气元件能较全面地反映相应实际元件的电气特性，仿真结果的可信度较高.

1 单闭环调速系统的组成及其工作原理

1.1 系统组成

带转速负反馈的单闭环直流调速系统的原理图如图1所示[1，7-8].

在图1中，A是调节器，当其选用P调节器时，图1就是一个有静差的单闭环调速系统;当其选用PI调节器时，图1就是一个无静差的单闭环调速系统;GT是触发器装置;UPE是由电力电子器件组成的变换器，其输入接三相(或单相)交流电，输出为可控的直流电压Ud;TG是测速发电机，它与电动机同轴安装.给定电位器Rp1，通常由一个稳压电源供电，以保证转速给定信号的精度.Rp2是为获得调速负反馈系数而设置的一个电位器.已知测速发电机输出电压Utg与电动机M的转速n成正比，即有Utg=Cnn，式中Cn为直流永磁式发电机的电动势常数.

假设电位器Rp2的分压系数为Kf，则反馈电压Un=KfUtg=KfCnn=n，式中=KfCn称为转速负反馈系数.注意，反馈信号Un与给定信号极性相反.

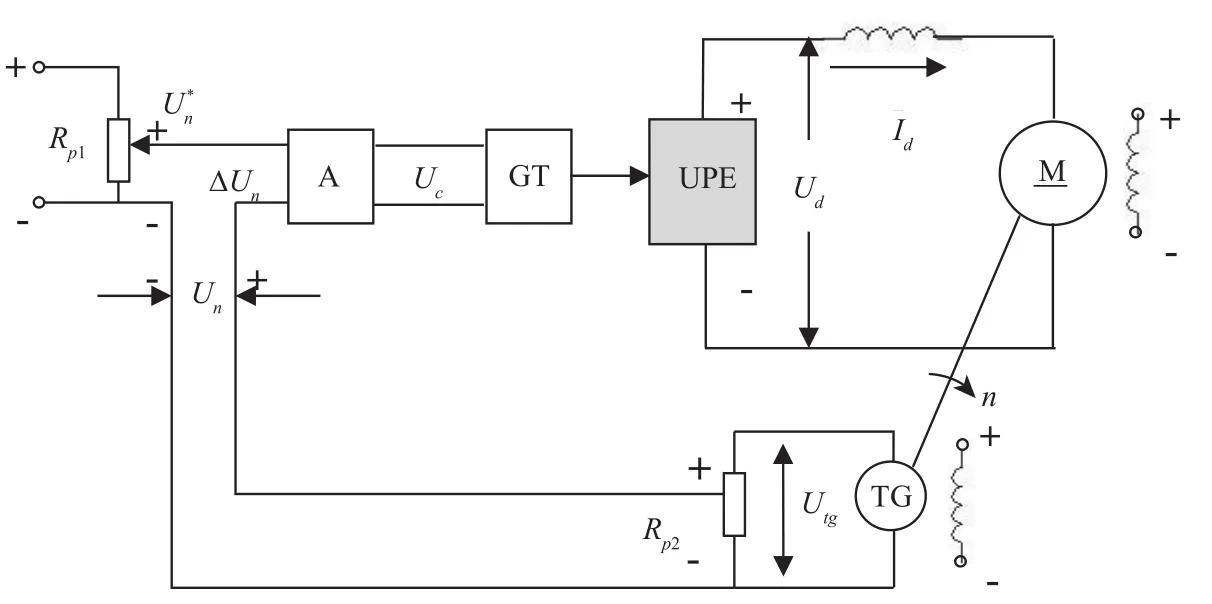
图1 转速负反馈单闭环直流调速系统原理图

1.2 系统工作原理

2 有静差转速单闭环直流调速系统的建模与仿真

2.1 系统的仿真建模

2.2 主电路仿真参数设置

由图2的仿真模型可知，主电路主要由三相对称交流电压源、晶闸管整流桥、平波电抗器、直流电动机等仿真模块组成[4-6].由于同步脉冲触发器与晶闸管整流桥是不可分割的两个环节，通常作为一个组合体来讨论，所以将触发器归到主电路进行建模.

1) 三相对称交流电压源.A相交流电源参数设置为交流峰值相电压取125 2 V、初相位设置成0°、频率为50 Hz，其他为默认值.B、C相交流电源参数设置方法与A相基本相同，除了将初相位设置成互差120°外，其他参数与A相相同，由此可得到三相对称交流电源.

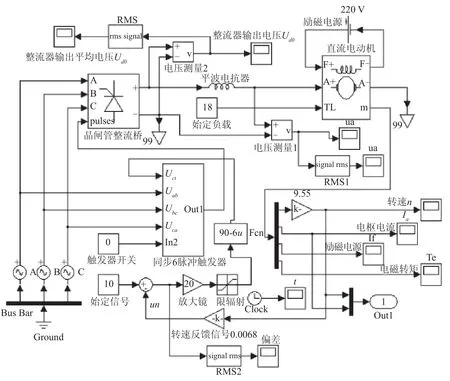
图2 有静差转速单闭环直流调速系统仿真模型

2) 晶闸管整流桥.使用该模块时，A、B、C均选择为输入端，DC端为输出端;“g(pulses)”端接受来自外部模块的触发信号，缓冲电阻Rs=10e5，缓冲电容Cs、内电阻Ron、内电感Lon等参数采用默认设置即可.

3) 同步脉冲触发器参数设置.同步脉冲触发器包括同步电源和6脉冲触发器.6脉冲触发器模块有5个输入端，如图3(a)所示.同步电源与6脉冲触发器及封装后的子系统符号如图3(b)所示.封装后的子系统符号，Uct为触发器控制信号，In2为触发器的开关输入信号，Out1端口输出脉冲信号，该端口与晶闸管整流桥的“g(pulses)”端相连，为晶闸管提供触发控制信号.同步6脉冲触发器参数设置的同步电压频率为60 Hz，脉冲宽度为10°，如再勾选了“Double pulsing”，触发器就能给出间隔60°的双脉冲信号.

4) 平波电抗器.平波电抗器的电感值是通过仿真实验比较后得到的优化参数.在此电感值设为5 mH.

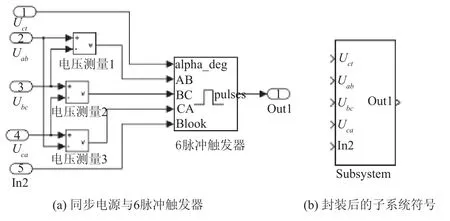
图3 同步脉冲触发器和封装后的子系统符号

5) 直流电动机.直流电动机的输出参数选择为转速n、电枢电流Ia、励磁电流If、电磁转矩Te4个信号.如果不指定直流电动机额定参数，可以采用默认设置.本设计选用的直流电动机额定参数为UN=220 V，IN=16 A，nN=1 500 r/min，电枢电阻Ra=1.5 Ω，飞轮惯量为GD2=22.5 N·m2，励磁电压Uf=220 V，励磁电流If=1.5 A.采用三相桥式全控整流电路，整流器内阻Rrec=0.6 Ω，平波电抗器Lp=200 mH，计算得到的电枢电感La=0.016 H、励磁电阻Rf=146.7 Ω、电枢绕组合励磁绕组互感Lof=0.76 H、电动机转动惯量J=0.57 kg·m3，额定负载转矩TL=18 N·m.

2.3 控制电路的建模与仿真参数设置

单闭环有静差转速负反馈调速系统的控制电路由给定信号、速度调节器、速度反馈等环节组成.仿真模型中根据需要另增加了限幅器和自定义的函数模块Fcn.限幅器的上下限根据需要设定，本模型中设为[-50，50];自定义的函数模块Fcn的函数关系式为90-6u，其中u是自定义函数模块的自变量符号.给定环节设置为10 rad/s;ASR采用P调节器，对该模块设置不同的参数即是改变ASR的放大倍数Kp，最终通过仿真优化得到比较合适的放大倍数选择范围;转速负反馈系数设为0.006 8，该系数由给定电压值和额定转速确定.

2.4 仿真结果分析

仿真中所选择的算法为ode23s，仿真开始时间为0 s，停止时间设为1.5 s，其他仿真参数设置为默认.当建模和仿真参数设置完成后，即可开始进行仿真.在额定转速信号=10，转速反馈系数=0.068，放大倍数Kp=5，10，20时的转速响应曲线如图4(a)所示、电流响应曲线如图4(b)所示(采用Matlab命令绘图).可以看到，随着放大器放大倍数Kp的增加，系统的稳态转速提高，稳态转速降落减小.从图4(b)中可以看出，由于没有电流的限制措施，在起动过程中电流仍很大可达970 A，这样大的起动电流很容易烧毁电动机，而且对过载能力低的晶闸管整流装置来说，更是不允许的.

由于晶闸管整流器控制的非线性，其输出电压只能在0～Udmax范围内变化.实验中当放大倍数取为200时，转速还没有出现严重的不稳定现象.如果再继续增大放大倍数Kp，如选择Kp=400时，控制系统则处于不稳定状态，转速就会出现严重的不稳定现象，如图4(c)所示.

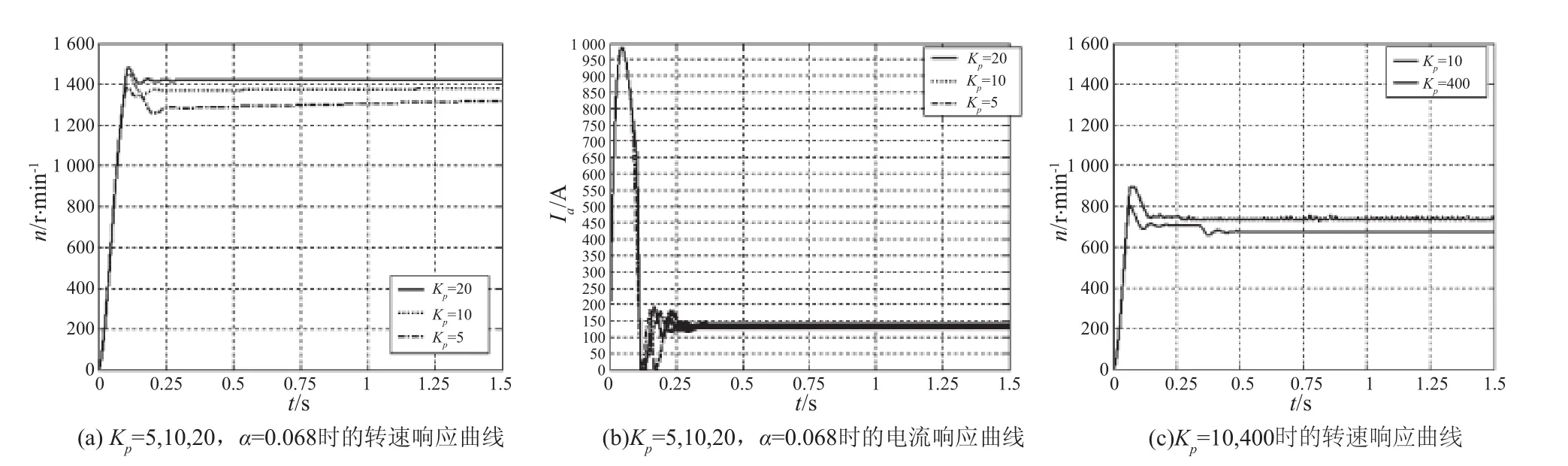
图4 不同放大倍数的有静差单闭环直流调速系统仿真结果(α=0.006 8，U*n=10)

3 无静差转速单闭环直流调速系统的建模与仿真

在有静差单闭环直流调速系统的电气原理结构图(图1)中，将ASR调节器换成PI调节器，就构成无静差转速单闭环直流调速系统.同样的，在有静差单闭环直流调速系统的仿真模型(见图3)中，将增益模块“Gain”改成PI仿真模块，就构成无静差单闭环直流调速系统的仿真模型.两者相比，仅是控制电路中转速调节器ASR采用的控制器类型不同，其余环节都是相同的.因此，无静差单闭环直流调速系统主电路的建模和参数设置方法都是跟有静差系统相同的，只是具体参数的设置值有所不同，这里不再一一赘述，仅重点介绍PI调节器的仿真建模、参数设置以及仿真分析结果.

3.1 PI控制器的仿真建模和参数设置

控制电路中PI调节器的仿真模型采用P调节器和I调节器相加得到.PI调节器的输入信号为转速给定和转速反馈信号之间的偏差ΔUn=-Un;其输出信号为触发器控制信号Uct.PI调节器的仿真模型及其封装后的子系统符号如图5(a)和5(b)所示.

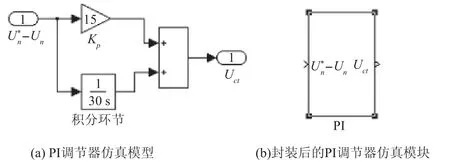
图5 PI调节器及其封装后的子系统符号

设系统的给定转速信号(实际上是电压信号)为150 rad/s，PI调节器的积分时间=30 s，其放大倍数Kp在保证系统稳定的前提下选择.系统无静差时，给定转速信号和转速反馈信号Un近似相等，即=Un=n.因此，转速反馈系数可以采用公式估算.这样，给定信号经过PI调节器，再通过限幅器和自定义函数90-6u后作为同步触发器的移相控制信号Uct.限幅器的范围仍设为[-50，50].

3.2 仿真结果分析

系统仿真中所选择的算法为ode23s，仿真开始时间为0 s，停止时间设为3 s，其他仿真参数设置为默认.取额定转速信号=150 V，放大倍数Kp=15，积分时间常数=30 s，转速负反馈系数=0.135时的转速响应曲线和电流响应曲线如图6所示.

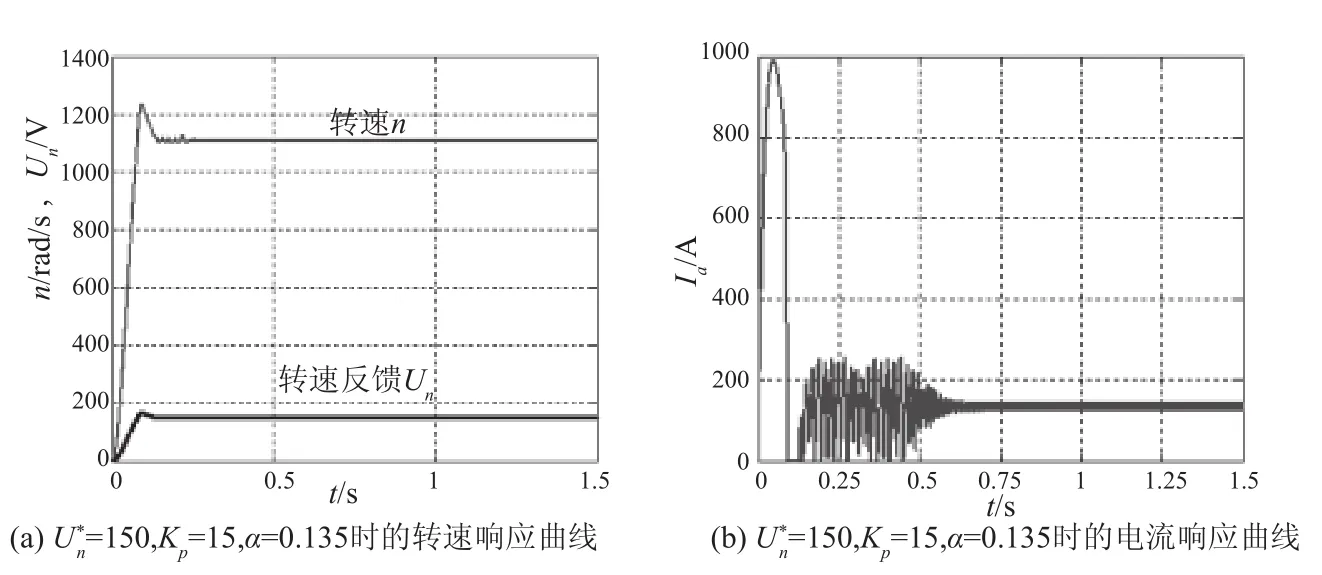
图6 PI控制转速无静差转速单闭环直流调速系统仿真结果

另外，从图6中可以看到，电流开始有一个突变，不过随着转速的增加，电流在逐渐减小，然后再经过PI调节器进行调节，电流基本上稳定，最后能够实现转速无静差.

4 结 论

在有静差转速负反馈单闭环直流调速系统中，由于采用P调节器，稳态时转速只能接近给定转速值，而不可能完全等于给定的转速值.提高开环增益只能减小转速降落而不能完全消除转速降落.为了完全消除转速降落，实现转速无静差调节，采用PI调节器代替P调节器，就构成无静差转速负反馈直流调速系统.而本文用Matlab/Simulink仿真技术实现了上述有静差和无静差转速单闭环直流调速系统的仿真建模，并给出了转速调节器参数改变时调速系统的仿真分析结果.实验结果表明，单闭环直流调速系统的调速性能仿真结果和理论上推导的调速性能相一致.另外，由于仿真模型是图形化的、面向对象的，非常适合教学实践环节和教学研究.

[1] 尚丽，马青，戴桂平，等. 运动控制系统[M]. 西安:西安电子科技大学出版社，2009.

[2] 方清城,罗中良,官峰,等. Matlab在运动控制系统实验教学中的应用[J]. 实验技术与管理,2007,24(1):73-75.

[3] 尚丽，淮文军. 基于Matlab/Simulink和GUI的运动控制系统虚拟实验平台设计[J]. 实验室研究与探索,2010,29(6):66-71.

[4] 张兴华. Simulink/PSB在“运动控制系统”实验教学中的应用[J]. 实验室研究与探索,2006,25(9):1077-1080.

[5] 寸巧萍. 自动控制系统实验教学中的仿真技术应用[J]. 实验科学与技术,2007,5(2):51-54.

[6] 石磊. MATLAB仿真在自动化专业教学中的应用[J]. 职业时空,2008,4(11):62.

[7] 张品秀,黄操军,梁春英,等. Matlab在电气工程专业实验教学中的应用[J]. 大庆师范学院学报,2010,30(3):44-47.

[8] 雷建军,金海燕,谭健苗,等. 计算机仿真实验在机能学实验教学中的应用[J]. 西北医学教育,2008,16(1):95-96.

[9] 汪建平,宋晓华. 大力发展仿真实验，改革机械设计基础实验教学[J]. 实验技术与管理,2006,23(8):85-87.

[10]张冰. 计算机仿真实验的教学应用及发展前景[J]. 华中科技大学学报,2005,24(3):116-118.

[11] 沈艳霞,赵芝璞,纪志成,等. Matlab/Simulink在运动控制系统教学中的应用[J]. 贵州大学学报:自然科学版,2005,22(4):435-438..

[12] 王印松，岑炜,李涛永,等. 基于Matlab/Simulink电力系统仿真工具箱的拓展[J]. 电力系统保护与控制,2009,37(2):84-88.