古典对称的语境特征及其意义

郭贵春，李 龙

（山西大学科学技术哲学研究中心，山西太原 030006）

古典对称的语境特征及其意义

郭贵春，李 龙

（山西大学科学技术哲学研究中心，山西太原 030006）

古典对称体现了欧氏几何图形之间的变换关系，在物理学各分支学科中有着广泛应用。文章通过定位古典对称，分析古典对称的结构特征，从而把握古典对称变换过程中的同一性。通过语义上升，把握不同对称现象之间的本质特征，扩展对称理论内容。

古典对称;语义分析;语境特征;意义

在欧几里得几何学中，存在着两个图形关于点、线之间的变换关系，就像人的左手和右手，当双手合拢时，各手指之间存在相互对应关系，我们就将其视为古典对称，这是人们在认识客观世界过程中总结出的直观规律。将图形赋予物理意义，古典对称的适用范围逐步扩大。随着物理学的发展，许多物理学现象与规律逐步纳入对称概念的范畴，使得对称有了更为丰富的内涵。本文通过使用语义分析方法，将古典对称看做是有关对称理论的元理论，在这一过程中，首先利用语义分析方法将古典对称的概念与客观实在进行联系，在概念与现象之间建立起客观的、准确的关联，规范古典对称所描述的内容;其次通过分析古典对称在物理学上的意义，找出古典对称在结构上的特征，界定域语言、操作语言和操作关系的适用范围，展现出科学知识对于特定知识体系结构的分析、解决问题的方法，为对称理论研究提供一个范式;最后本文在把握对称关系结构同一性的基础上，通过将对称概念在语义上上升，把握对称在物理学各个分支学科的应用，提供了一种解释和解决物理学难题的方法。而在物理学各个分支学科的研究过程中，对称作为一种物理学分析方法几乎贯穿于物理学研究的各个领域。那么，我们抛开学科界限，把握对称所展示出的本质特征，通过扩大古典对称语境，将物理学各个分支学科的对称现象加以归纳和解释，从而构造出一个横断于物理学研究的纲领，本文的意义也就在此。

一 古典对称的定位及数学分析

随着物理学的发展，人们将电磁学、原子物理学和相对论等诸多物理学的分支学科中的相似命题归纳到对称这个概念的范畴之内，扩大了对称这一概念的内涵，并就这个概念进行全新阐释。当对称概念摆脱传统观念的束缚后，脱离了经验层面上可观察两个图形的完全重合这一标准，将不变量与守恒量引入理论，充分显示出该理论所具备严谨的逻辑性和完备性，使得对称理论在数学、物理学研究中赋予更为广阔的应用范围和丰富的结论。纵观几何学、牛顿力学、电磁学、粒子物理学等学科，每个学科中蕴含着各不相同的研究思想与研究方法，对称在这些学科中所体现的意义也是千差万别的，这就需要用一个横断研究的方法来阐述对称概念本身及其意义。而语境分析则正好可以完成这个使命，因为“任何要素都只有在与其他关联存在的具体的或历史的语境中，才是富有生命力的。”［1］

古典对称就本质上来说是关于几何图形的对称，其内容来源于人类自身对环境的观察与总结，是最为直观的对称类型，也是人们在数学、物理学研究中所认识到的最初级的对称，前面所提到的近代物理学中的诸多类型的对称就是以此为基础。

古典对称创立与发展的基础是我们日常生活中的空间，欧几里得几何对空间的描述由于符合人们对所处空间的认识而被广泛接受。欧氏几何中定义了维度这个概念，并规定我们所处的空间是三个独立的维度，且在各个维度上都具有各向同性。这些也就构成了我们关于空间这一概念的认识基础，同时也是古典对称研究的数学基础。在划分古典对称的类型时，不同的划分方式将引导出不同的结论。古典对称存在以下几种划分方法:

（1）按照对称图形的个体数量来说，有单一物体对称，即图形的一部分与另一部分之间的对称;有两个物体之间的对称;有一组图形（图形数量≥2）与另一组图形之间的对称。

（2）就图形之间的对称关系来说，有关点对称的;关于直线对称的;关于平面对称的。例如，我们日常生活中的镜像对称，自己和镜子中的像所具有的对称。

（3）按照对称变化是否连续来划分。例如平面图形中的圆将会根据其自身的任意一条直径产生对称变换关系，当直接连续变换时，圆中的对称关系也是连续变换的;而图形不能满足连续变换规律时则认为是不连续的。

（4）按照空间维度进行划分，这也是最常见的划分方法。在欧氏几何中将空间确定为三个相互不同的维度，图形之间的对称关系存在于一维、二维和三维空间。

以上所提及的古典对称的不同划分方法，分别代表了不同的分析问题的角度与分析方法，其侧重点虽各不相同，但并不排斥，如二维平面中的圆自身的对称性，从维度上说是二维的，从数量上说是单体，从对称种类上说是点或直线对称，对称关系可以看做是连续的。在古典对称研究中所体现出的方式和结论是大致相同的。当我们谈及两个大小、形状相同的几何图形的对称性时，通常情况下是指这两个图形通过某个操作（平移或转动）后可以完全重合。古典对称的研究通常以人们所熟知且容易区分的空间维度作为主要的划分标准。对于平面图形的重合，两个图形的重合不会有物理上的障碍，即它们无论是作为几何的符号还是作为实际存在的物理客体来说都是会重合的。当对于三维图形来说，三维空间的图形对称还需要附加一些条件，因为三维空间中所体现出的对称性将更加丰富。在三维空间中不仅存在着平移对称与转动对称，还有一种特殊的对称——螺旋对称，螺距均匀的圆柱形螺旋线有旋转对称性，其主要特征为将其沿轴线提升一个距离X及旋转一个角度α后的新螺线与原螺线重合。可见，古典对称的发展已经颠覆了我们传统思维中的概念，虽然仍基于自身观察，但是已经逐步远离人们的经验，变得更加逻辑化。当我们谈论不同类型的古典对称时，由于语境的不同，古典对称所指的内容也相差极大。

当我们用传统几何学的方法证明图形的对称时，首先观察图形是否“相似”，然后通过欧氏几何中所预设的公理、定律等条件逐步完成全等的证明过程。在这个演绎的、综合的几何证明过程中，被论证的公理被认为是“自明之理”，这个“自明之理”以及由此推导出的定理本身就缺乏严密的逻辑起点，故我们认为欧氏几何所证明的图形对称也仅仅是从总体上粗略地比较两个图形是否完全重合而已。在欧几里得所创建的几何大厦中，给出了大量的真理，但在其理论体系中并未解释为什么会是这个样子，也没有指出是如何发现这些规律的。［2］欧几里得所做的证明也仅仅可以告诉我们什么样的图形是可以看作对称的，甚至可以告诉我们这类对称图形有哪些性质，但在他的理论中并没有阐述图形对称的原因。

解析几何的出现，为我们研究古典对称提供了一个新的范式。在这个新范式中，古典对称理论有了新的量化标准，这就提供了研究古典对称的具体操作步骤，从而简化了研究手段，使得研究结果更加精确。解析几何开创了由传统的几何、算术到普遍的数学的传统。

在几何图形的数学化分析过程中，图形中的每个点都与坐标相确定，可以将确定的几何图形与空间位置用准确的数值来描述，通过简单的比对函数数值来确定图形之间的关系，甚至可以将图形中的变化情况用数字进行描述。在整个分析过程中，解析几何为我们展示了一个分析的几何过程而并非综合的几何过程。［3］在解析几何中可以将其描述为一个图形经过一个数学变化后与另一个图形保持一致，那么我们将图形间的几何关系转化为一种数学关系。关于几何对称问题，有点与点之间的对称关系，也存在图形之间的对称关系。而我们可以将图形之间的对称看作是一个集合中的点经过对称操作后与另一组集合之中的点存在着一一对应关系，那么我们可以认为图形之间的对称包含点之间的对称关系。

二维空间中点对称的数学变化可以由下列算式描述:

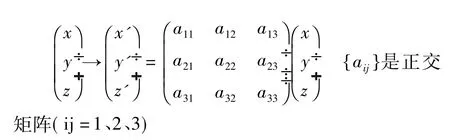
从古典对称变换的数学公式中可以看出，我们以研究点的对称操作为基础，将点与点之间的对称变换看作是一个正交矩阵作用在这个点上的过程。其中，正交矩阵的模存在着多种不同的取值情况，分别代表了图形在各自维度上所进行的缩放。在对称变换过程中，正交矩阵的模为1，表明两个点到对称点的距离是相同的，如平面中一个圆的两个半圆关于圆心的对称。当我们在欧氏几何所描述的空间中研究对称现象时，古典对称在不同维度中所体现出的公式差异，仅仅是在描述点的函数中加入新的独立变量，且在正交矩阵中做出相应变化。

利用解析几何方法分析古典对称问题，先利用数组将图形中的点在坐标轴上定位，然后将图形看做是空间中的点按照一定规律所排列的集合，用φ（x，y）或 φ（x，y，z）来表示，则对称变换公式可改写成 φ（x，y）→φ（x'，y'）={aij}φ（x，y）或 φ（x，y，z）→φ（x'，y'，z'）={aijk}φ（x，y，z）。在对称变换前后，函数中的自变量发生改变是由于图形的位置发生改变;变化前后图形保持着一一对应关系，用函数形式的不变来表征形状并未发生改变;在变换过程中引入了正交矩阵，说明图形没有进行缩放。整个古典对称变换的过程是一个分析的过程，而不是欧氏几何证明中所体现出的综合的过程。

二 古典对称的物理意义与结构特征

古典对称在数学分析过程中所体现出严谨的逻辑性和精确性为物理学所借鉴，将古典对称理论引入物理学研究之中，并辅以物理学分析的合理性，使古典对称理论显示出强大的工具性，从而使得对称理论在物理学中得到长足发展，极大地丰富了古典对称理论的内涵，主要体现在以下几个方面:

第一，古典对称利用其直观化的优势，通过赋予几何图形以物理意义，从而引导物理问题寻求几何化求解方法，从而将物理问题较为直观地呈现，使物理思维变得更加明晰，简化分析物理问题的过程，这就是从二十世纪初一直延续到现在关于对称性问题研究的趋势。

第二，古典对称理论在固体物理、结晶学等学科中的应用。这里，我们着重研究对称操作的个数。当一个图形在某一正交变换下保持不变时，我们就可以将这个正交变换看作是一个对称操作，当一个图形可以完成更多的对称操作而保持其不变性时，该图形就表现出更高的对称性，例如平面等腰三角形所满足的对称操作个数明显小于圆所满足的对称操作个数，则可知等腰三角形所具有的对称性小于圆的对称性。在结晶学和固体物理学中，晶体的宏观性质就是由内部格子的对称性所决定的。不同的晶体之间具有不同的对称性型，可以根据晶体的对称特点划分出不同的晶族和晶系;晶体对称性从本质上来说取决于内部格子的构造，所以，晶体的各项物理性质都是取决于其组成质点的种类和排列方式，因此晶体中凡是具有方向性的物理性质，如折射率、电导率和硬度等都会呈现出对称关系。晶体的对称性决定并影响着晶体中涉及几何和物理两方面的一切性质;反之，可以通过晶体的几何外形以及它们的一些物理性质来正确地确定晶体的对称性。

第三，随着古典对称理论的发展，对称已经不仅仅是在可观察层面上的图案重合，通过继承对称关系中的逻辑性及其推导过程，对称理论已经逐渐远离经验层面而继续向物理学各领域渗透。在物理学的各个分支学科中，人们利用对称变换推导并总结出不变量与守恒量，并在随后的理论与实践中得到验证，使人们逐步接受对称性，并坚信对称性的普遍存在，从而发展对称理论。接着积极地在各种有意义的现象之间建立关联，充分利用对称理论分析问题，并预测未知现象。

第四，利用对称性，在两个看似不同的对象中寻找它们的共同特征，并建立相互关联。一旦我们确定两事物之间存在某种对称性，于是通过确定这个对象的特征，利用对称性之间的相互联系来推导出另一对象的相应特征。这样，我们发现从表面上看上去彼此无关的对象，如果将它们放在对称性语境中加以考察，可能会发现其中存在的某些遗漏和缺陷，以此更加全面地了解对象的更多特征。例如，我们日常生活中的空间与时间的问题，通常人们会认为空间和时间是相差很大的两个对象，牛顿力学关于空间和时间的研究尤为丰富，指出:它们分别属于两个不同的量纲，代表着不同的物理意义，用不同的单位来度量，实验中使用不同的仪器来测量。而爱因斯坦看到了空间和时间之间的一些共同特征，认定它们之间存在着某种对称性，然后通过对称理论将时间统一为第四维度的空间，从而扩展了相对论的内容。在19世纪末20世纪初，物理学家利用对称原理发现了当时存在于物理学中若干重大佯谬，并随之做出相应的修正。［4］在上个世纪中后叶，利用对称理论大胆预测了当时尚未发现的微观粒子。

最后，推动数学分支学科－群论的发展。古典对称变换操作中，透过图形变换这一表象，把握其操作后保持不变这一特征。牛顿力学与量子力学因可以准确地描述宏观与微观世界中的物理规律而被广泛地认同，在经典宏观系统与微观系统中的物理特征分别由拉氏函数与哈密顿量决定，宏观与微观世界的对称性分别表现为拉氏函数与哈密顿量在变换中保持不变的集合来描述。这样，在不同的变换规则下产生出不同的群，对称变换的集合描写系统的全部对称性质。根据系统的对称性质，通过群论方法研究，可以直接得到系统许多精确的、与系统无关的重要性质。［5］群论的出现为物理学提供了一个有效的数学工具，而物理学的发展反作用于群论，推动群论的深入研究。

任何科学知识都是通过特定的科学语言系统获得其自身存在的物质外壳，从而展现它描述，解释和把握客观世界规律的本质。［6］4

对称性作为物理学中的普适原理之一，描述对称性原理的科学语言在结构上存在着两重性，域语言（area language）在深层地语义结构内在地规定了相应知识系统所涉及的范围，是一种定性的描述;而操作语言（operating language）在表层句法上直接地规定了相应知识系统在其研究领域的操作规则，是一种定量描述。一个确定的知识系统图景就可以用表示为:St=∑（OdA），其中O表示操作语言，它作用于域语言A。d表示由该知识系统所允许进行描述的确定操作关系。下标t表示这一系统的特定发展阶段或时期。∑是整个研究域和这一系统中各操作要素的集合算符。［6］5

就古典对称来说，其研究对象为日常生活中可观察的几何图形，这些几何图形存在于欧几里得所规定的一维、二维和三维各向同性的空间中。科学哲学中关于对象的划分有着多种不同的方式，在这里我们参照弗雷格关于对象的划分标准，他将心理学对象与逻辑对象，主观对象与客观对象明确区分开来，将对象划分为三类:物理的（物质客体）、心里的（灵魂）和抽象的（像数这样的抽象概念）。经验主义把“数”这个概念视为外在事物的抽象描述，这样将数与物质客体进行联系，并且可以被用于外在的物理对象等。［7］对称图形中的每个点都是物质客体，而将图形看做是一系列点按照一定规律排列所组成的集合，函数在空间中的轨迹与图形相对应，而这个函数则应当被视为抽象客体。对称变化过程中的操作语言，在公式中表示为正交算符，它代表了一种数学变化具体操作过程。

科学实在论者坚信，科学为我们所展示的途径是真实的，它的每个细节都值得我们信赖，科学中假设的实体也是实在的，科学是通过一个个的发现而获得进步的。［8］哥白尼、开普勒、笛卡儿等人都认为自然界的某些现象是与数学十分吻合的，他们甚至认为上帝不仅创造世界，而且也创造了与人相一致的数学思维。科学实在论者继承并发展了柏拉图将数字看做是共相的观点，认为数学是独立于数学家的运算以及普遍人的思考，数学是对客观存在的实体的科学研究，就像是物理学对实体研究一样。

在研究古典对称变化过程的数学公式中，描述几何图形中点的坐标或者点之间位置相互关系利用函数来表示，这是弗雷格所定义的概念客体;古典对称变换的操作语言矩阵也是概念客体－数。数通常被认为是内在最直观的对象，就数的关系的运算通常被认为是精神的活动。精神在这种活动中就把它最特有的关系，或者最为本质的关系以最直观的方式展现出来。算术是一种分析科学，因为在算术对象中出现的一切关联和区别，都并非在对象本身中，而完全是从外面作用于对象的。它并没有具体的对象，具体对象有自在的内在关系，起初隐藏着不被认知，不是在有关对象的直接观念中就呈现出来，而是要由认知的努力而获得。［9］我们关于古典对称的系统认识是建立在数学基础之上，即一个描述几何图形的状态函数在对称操作下保持不变。

三 古典对称的句法及其意义

古典对称是以日常生活中的观察现象为基础，通过现象总结出规律。而一个观测（总结出）的理论可能会详细地说明在特定条件下所发生的现象，并且不仅在概念上，在上下文中可能真正地给出局部特征;而定律则会有更严格的要求，它不仅会列出作为真的可能性条件，而且会要求给出在上下文中什么是真的可能性的完整特征。［10］这些可观察的物理量、客观实在不仅构成科学语言中的“所指”，还称为人类日常生活所形成的常识的基础。科学、哲学以及理性思维都必须以常识为出发点，［11］但常识并非是一个可靠的出发点，因为常识其不具备物质客体的特征，是不为经验论者和唯名论者所认同的。人类在获取知识的过程中，以常识为出发点，获得进步的手段是批判。传统的经验论者和唯名论者都承认物质客体的客观性与实在性，而概念客体是从日常生活中总结出来的规律，不具有客观实体的特征。

人们在观察客观世界时仅仅得到了关于世界的外在的、直观的表象，并将概念、词项和客观实在相对应，构成语义分析中所指的内容;而科学理论要求掌握其内在的、具体的意义，通过利用句法规则构成能指的形式。语义分析正是一个将表层语言的句法结构与深层本质的语义结构之间的内在关联获得实现。［12］

在古典对称中，对称变换构成科学理论语义分析中“能指”的内容，正交矩阵则形成“能指”的形式;几何图形、状态函数、重合、不变量等构成“所指”的内容，几何图形中点的排列方式和状态函数中点所形成的轨迹则称为“所指”的形式。通过分析所指内容中的几何图形，我们可以得到一些表象的特征，也是初级特征。而几何图形的更深层特征只有通过句法的形式系统，即利用一个操作域，图形经过变化后将始末状态连接起来，操作域构成了连接始末状态的桥梁。就像化学反应是连接反应物与生成物的桥梁一样，在没有发生化学反应之前，只能观察到物质所具有的物理特性，当发生化学反应后，其所具有的深层的化学性质才能以体现。古典对称就是利用对称操作将静态的几何图形转化为动态的演化过程。在这个过程中，几何图形的位置发生的改变，这一过程通过改变状态函数φ中的坐标来实现;几何图形变化后所处的位置由正交矩阵所确定。而在古典对称过程中，几何图形的形状和大小并没有发生改变。通过分析几何图形的状态函数φ，当变化前后φ相同时，则表示图形的形状不变;而几何图形的大小不变则是通过变换过程中，正交矩阵的模为1来实现的。在古典对称中，虽然图形的位置发生改变，但是图形的大小与形状并没有改变，那么在这里古典对称体现出了一种经过变换后的不变性。

随着现代科学越来越远离经验的发展，科学理论已经被人们视为表述为真值的符号网络。在这个网络的构架过程中，越来越多的客观实在抽象地归纳于系统之中，使这个符号网络具有更高的层次和更复杂的结构。在物理学各分支学科如牛顿力学、电磁学、量子力学等领域，古典对称现身其中并发挥着不可替代的作用，使得对称理论的对象得到扩充，从而导致域语言、操作语言和操作关系都随着发生改变。在扩展过程中，古典对称的理论内核－古典对称的语义分析并未发生改变，我们应当把深层的语义分析看作是对真理的揭示，那么科学形式表述的结构同一性就比语义分析“更基本”。［6］40古典对称在物理学的发展中，摒弃原来仅依靠几何图形而完成的对称操作，利用逻辑关系，开始逐步利用这种对称操作，将物理学中看似不相关的两个对象联系在一起，从而保持句法结构上的同一性，并随之规范操作语言和操作关系，通过域语言的上升和引入新的术语和新的语义和句法的规范性，扩展了对称这一概念的语境范围，使对称理论在动态变化中继续保持域语言、操作语言与操作关系之间的协调性。

语义分析方法在哲学背景上从来都不是中性的，它始终与本体论的假设联系在一起。［13］利用语义分析方法分析古典对称问题，在图形与规律之间利用科学语言将其规范化描述，在它们之间建立起多层次、具有逻辑关系的桥梁，使二者可以在科学解释中形成相互转化的过程。

在笛卡儿尚未使用数形结合的思想描述几何图形之前，当在传统视野下判断古典对称关系时，仅仅依靠欧氏空间中对几何图形的观察，这是非常不准确的;更糟糕的是，即使去推导或证明对称关系，那也是通过欧几里得所创立的几何学来判断。众所周知，欧氏几何是建立在一些自明之理或公设基础之上的，这些公理或公设本身也是建立在常识基础之上。常识所描述的客观世界在一些情况下是准确的，但有时所描述的客观世界也是不准确的，如两千多年前亚里士多德曾认为重的物体下落的快。那么基于常识基础的对称关系判断则表现出了不完备，或者说是逻辑基础不严密的;而使用了解析几何的方法，不仅可以将图形数学化描述，而且将对称变化的过程进行数学化描述，这样，古典对称自身则具备了准确的数学基础和完备的逻辑基础。

观察总是不精确的，而理论却做出绝对精确的断定。［14］在解析几何中引入了坐标轴与坐标系，将几何图形放入坐标轴或坐标系中，为图形中的点与坐标形成一一对应关系，这样就可以用代数确定几何图形。在代数与图形的结合过程中，可以利用数学准确地表明图形与图形之间的关系，那么对称关系就可以表述为一个数学公式，将古典对称过程中的几何图形之间是否重合翻译成解析几何中数值是否相等，这样就可以通过数字对古典对称过程进行准确的分析与判断。古典对称自身则具备准确的数学基础。

古典对称仅仅建立在逻辑基础之上仍然是不够的，要完成将古典对称作为普遍性原理，还需要我们要以毫无间断的连续的思维运动来思考问题，这样探索古典对称的过程才会更加完备。这是由于那些并非从自明之理中直接演绎出来的真理，如果要保证它的确定性，必须遵守一个连续的推导过程。当推论的连续步骤过多时，如果我们到达真理，已经不能完整地重复推导过程，这样的话，需要用连续思维来弥补这个过程的缺陷。以过程A→B→C→D为例来加以说明，由事物A可以推导出事物B，紧接着可以推导出事物C，然后可以推导出事物D，这是一个连贯的逻辑推导过程，当我们忽视B→C这一环节，那么我们是不能轻率地给出A与D之间的关系，在这里A与D之间的关系推导就丧失其确定性，因此我们有必要再重新回顾A到D的整个推导过程。仅仅通过连贯的逻辑推导是不能得到真理的，笛卡儿指出，要达到事物之真理，需要通过双重途径，一条途径是我们刚才提到的演绎，另一条途径是我们的经验。故还需要一个列举或归纳，这个过程的意义在于我们可以得到明显而确定的结论，从而避免由于粗心而忽略某些问题。

四 结论

通过以上分析可以看出，古典对称问题可以看做是对称问题的一个基础问题，率先引入了数学中的算术部分，将对称关系以数字的形式呈现在我们面前，从而开创了古典对称问题的逻辑传统，为我们继续研究对称理论提供了一个良好的范式。在把握古典对称语义特征的背景下，将古典对称问题进行演绎与推理，使对称理论扩展为一个普适理论，逐步融入自然科学之中。而在古典对称问题中所体现出的语义学分析与解决问题的方法，为研究其他领域的对称问题提供了很好的借鉴作用。

对称问题虽然起源于数学研究，但是在物理学中有着十分广泛的应用。爱因斯坦在回顾物理学的研究历程之后指出，当物理学描述客观世界时，不得不借助于分析几何学，那么我们可以将物理学的对称问题转化为几何学的对称问题来加以研究，物理问题的几何化研究方法从二十世纪初一直延续到今天，其重要性也逐渐体现出来，如利用对称性原理发现守恒定律，推导出某些未被观察到的粒子等。物理学中各事物之间的对称关系并不像几何图形一样直观明了，事物之间的相互关系往往隐藏在系统内部，我们通过把握物质及物质所体现出来的不同的运动状态，将看似毫不相关的事物，用对称关系将它们联系在一起，这样就使得物理学所研究的问题变得更加简化。由于对称只需要考察事物的始末状态，而无需考虑其过程中的繁琐细节，可以根据某个对象通过对称性理论去推测另一对象在某方面的特征，然后进行检验。这样可以跳过繁琐的细节，有效地简化解决问题的过程，从而体现出对称性理论的优越性，它已经在物理学的理论研究中发挥出重要的作用。

［1］郭贵春．语境分析的方法论意义［J］．山西大学学报，2000（3）:1．

［2］［英］罗杰·彭罗斯．通向实在之路［M］．王文浩，译．长沙:湖南科学技术出版社，2008:19．

［3］［法］笛卡儿．笛卡儿几何［M］．袁向东，译．北京:北京大学出版社，2009:78．

［4］孙宗杨．物理学中的对称性［M］．合肥:中国科学技术大学出版社，2009:5．

［5］马中骐．物理学中的群论［M］．北京:科学出版社，2009:18．

［6］郭贵春．科学知识动力学［M］．武汉:华中师范大学出版社，1992．

［7］江 怡．当代西方数学哲学中的实在论与反实在论［J］．浙江学刊，2004（2）:75．

［8］Bas C．van Fraassen．The scientific image［M］．Oxford:Oxford university press，1980:6．

［9］［德］黑格尔．逻辑学［M］．杨一之，译．北京:商务印书馆，2010:226．

［10］Theo A F，Kuipers．General philosophy of Science:Focal issues［M］．Ansterdam:Elsevier，2007:8．

［11］［英］卡尔·波普尔．客观知识——一个进化论的研究［M］．舒炜光，译．上海:上海译文出版社，1987:35．

［12］郭贵春．科学理论的语义分析——科学实在论的重要研究方法［J］．社会科学研究，1991（3）:44．

［13］郭贵春．语义分析方法的本质［J］．科学技术与辩证法，1990（2）:4．

［14］［英］卡尔·波普尔．猜想与反驳——科学知识的增长［M］．傅季重，译．上海:上海译文出版社，2001:265．

The Contextual Features and Significance of Classical Symmetry

GUO Gui－chun，LI Long
（Research Center for Philosophy of Science and Technology，Shanxi University，Taiyuan 030006，China）

Classical symmetry can materialize the transformation relation between Euclidean geometry figures，so it has a wide application in various branches of physics．In this paper，we will locate the classical symmetry and analyze the structural features of classical symmetry，so as to grasp the identity in classical symmetry transformation．Through the rise of semantic meaning，we can grasp the essential features in different symmetry phenomenon，and extend contents of symmetry theory．

classical symmetry;semantic analysis;contextual features;significance

（责任编辑 李雪枫）

O141

A

1000－5935（2011）02－0001－06

2010－12－22

郭贵春（1952－），男，山西沁县人，山西大学科学技术哲学研究中心教授，博士生导师，主要从事科学哲学研究;

李 龙（1982－），男，山西长治人，山西大学科学技术哲学研究中心，博士研究生，从事科学技术哲学研究。

·教育学与心理学研究·