二维EMD方法在物化探数据处理中的应用研究——以云南个旧地区为例
2011-01-10何丽娟
何丽娟,张 毅,张 焱
(1.中海石油(中国)有限公司湛江分公司研究院,广东 湛江 524054;2.中山大学地球科学系,广州 510275)
0 引言
在资源勘查与预测评价工作中,物化探数据的处理至关重要。如何从复杂的叠加异常中分离出单纯由勘探目标引起的异常,是目前勘查工作中最主要和最困难的问题;异常的有效分离有助于选取合理的勘探目标。
1998年,美籍华人Norden E Huang等[1]提出了Hilbert-Huang变换(HHT)。HHT是一种分析非线性、非平稳信号的新方法,它引入了固有模态函数(Intrinsic Mode Function,简称IMF)的概念,在经验模式分解(Empirieal Mode Deeomposition,简称EMD)的基础上,对每个IMF进行Hilbert变换得到瞬时频率,从而将信号精确表示为时间-频率-幅度的分布,称为Hilbert谱。
Hilbert-Huang变换提出以后,引起了人们的广泛关注,目前己成为信号分析领域的热门话题。在应用方面,HHT得到了快速的发展。2003年,J.C.Nunes等[2]在一维H HT基础上引出二维HHT,并将二维HHT成功地用于图像分析中,从而进一步地推动了HHT应用领域的发展。
在实际找矿生产中,剖面重力异常数据所显示的找矿信息是远远不够的,因此为了提供有效的找矿信息,对平面异常信息的处理至关重要。本文将引用文献[2]的有关二维HHT,研究它的二维经验模态分解(Bidimensional Empirical Mode Decomposition,简称BEMD)理论,将二维EMD方法应用到云南个旧地区物化探数据的处理中。
1 二维经验模态分解(BEMD)
1.1 Hilbert-Huang变换(HHT)
Hilbert-Huang变换(Hilbert-Huang Transform,简称HHT)由经验模态分解(Empirical Mode Decomposition,简称EMD)和Hilbert谱分析两部分组成。HHT的基本内容分为两个过程:①通过经验模态分解方法将信号分解成有限数目具有一定特征的固有模态函数(Intrinsic Model Function,简称IMF);②对每个IMF进行Hilbert变换并求解出瞬时频率,得到信号时间-频率平面上的能量分布(时间-频率-振幅),即Hilbert谱。
对于信号X(t),经EMD分解后可表示为:
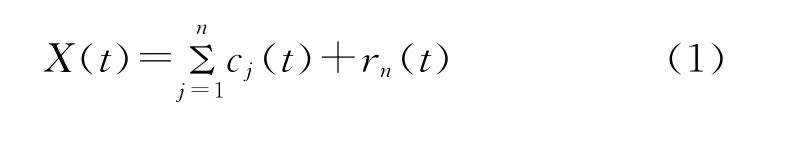
其中,rn(t)为残余分量;cj(t)为第j个固有模态函数(IMF),它满足2个基本条件:①信号过0点的个数与极值点的个数相等或最多相差1个;②在任一时间点上,由信号极大值拟合的上包络线和极小值拟合的下包络线的局部均值为0。
对每一个固有模态函数分量cj(t)进行Hilbert变换,可得到时间-频率平面上的幅度分布,即Hilbert谱。
1.2 二维经验模态分解
Nunes(2003)等[2]在一维H HT基础上提出二维经验模态分解方法(BEMD)。目前,很多文章提出二维EMD方法的分解方式,有行列分解法[3]、面分解方法[4-5]和方向EMD分解法[6]等。本文采用文献[3]中提出的行列分解法实现二维EMD方法,其基本思想是先将二维数组的每一行和每一列看成是一维数据,用一维EMD方法分别对它们进行分解,从而提取出二维数组的行、列数据的细节。筛分算法流程图见图1。
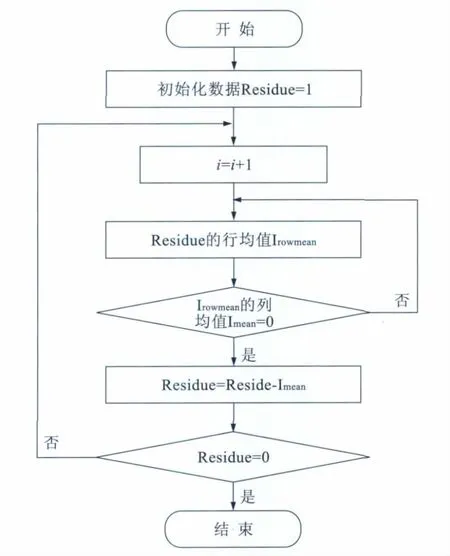
图1 二维EMD行列分解法流程图Fig.1 Flow sheet of EMD decomposition
2 研究区地质概况
云南个旧锡、铜多金属矿区地处云南省东南部,位居环太平洋成矿带与地中海—喜马拉雅成矿带的交汇处,是我国滇东南锡矿带上最重要、规模最大的锡多金属矿集区之一。区域地质构造位置为扬子准地台、华南褶皱系及唐古拉—昌都—兰坪—思茅褶皱系三大地质构造单元汇聚地带之华南褶皱系右江地槽褶皱带西南端(图2)[7]。
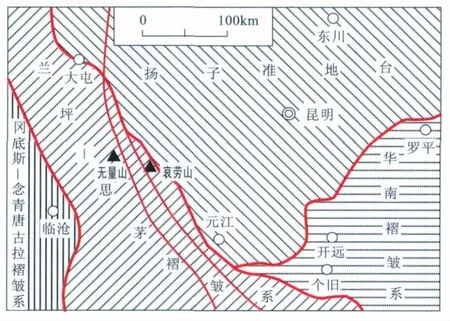
图2 个旧锡多金属矿区大地构造单元示意图(据肖凡,2008修改)Fig.2 Sketch showing the geotecnic position of Gejiu Sn-polymetallic district
研究区内主要断裂构造有:①NW向的红河断裂,该断裂是滇东南成矿区的南部边界,也是南盘江—右江盆地与哀牢山地块(推覆体)的南西分界线,走向320°~340°,倾向NE,倾角较陡(60°~85°)断裂总长>700 km;断裂南西侧出露哀牢山群,北东侧出露中生界-新生界;②SN向的小江断裂,该断裂是纵贯云南东部、向北延伸至川西的一条区域性超壳深大断裂,也是我国强烈的地震带之一。
地质体的物性差异是物探工作有效性的基本前提。据前人资料[8],个旧地区的岩矿石密度有以下特点:①地表土和第三系的密度最低,为1.90~2.07 g/cm3;②三叠系、二叠系、泥盆系的平均密度为2.70~2.80 g/cm3;③花岗岩平均密度比围岩低,为0.15~0.24 g/cm3;④锡矿石密度最大,为4.52 g/cm3;⑤基性、超基性岩为3.0~3.1 g/cm3。
3 应用效果分析
本文采用个旧地区1∶20万水系沉积物Sn元素和重力异常数据作为分析对象。在MATLAB中,编写程序完成对Sn元素和重力异常数据的处理。其中,固有和重力异常数据的处理。其中,固有模态函数(IMF)个数设定为2个,固有模态筛选次数为800次。IMF个数设定为2个是因为过多的固有模态函数不具有实际物理意义,反之,则忽略了化探异常细节。
3.1 二维EMD方法在化探数据处理中的应用
对Sn的水系沉积物地球化学异常数据进行二维EMD分解,得到3组数据,分别为第一级固有模态函数(IMF1),第二级固有模态函数(IMF2)和剩余分量(residue)。
在MORPAS中得到这3组化探数据对应的色阶图(图3)。图3a为个旧地区Sn水系沉积物地球化学异常,图3b,c,d分别为个旧地区Sn化探异常的第一级局部异常、第二级局部异常和区域异常。
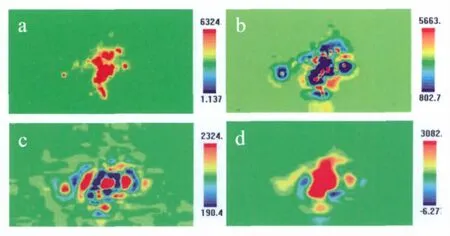
图3 个旧地区Sn的水系沉积物测量数据分解结果图Fig.3 EDM decoposition diagram of Sn distribution in river sediments
在Map GIS中,对Sn水系沉积物地球化学异常等值线及分解得到的3组化探异常等值线和Sn矿分布进行叠加,得到4幅叠加图,如图4所示。在这4幅图中,矿床(点)用蓝色圆圈表示;化探异常等值线用红色或蓝色线条表示,其中,异常值高于800用红色线条表示,低于800用蓝色线条表示。从这4个图中可以看出:①矿点落在图4b和图4c的异常等值线内,这说明图4b和图4c反映浅部地质信息;另外,图4a中一个大的异常圈闭经分离后形态发生很大变化,形成了3~4个小的异常区及SN向的异常带(图4b),对比区域场结果(图4d),图4a中异常是由区域效应造成的,经分离后,图4b和图4c较好地体现了局部场的特点;②图4a中,对本区异常无方向可言,经分离后,图4d中异常呈SN向的特点,区域场反映深部地质信息。据上所述,二维EMD分解成功地分离了Sn的地球化学异常,使分解得到的每一种分量都具有一定的物理意义。
3.2 二维EMD方法在物探数据处理中的应用
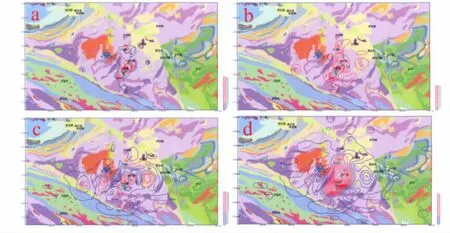
图4 个旧地区Sn的水系沉积物化探异常等值线与锡矿分布图Fig.4 Map showing river sediment Sn anomaly contour and distribution of Sn deposits
对研究区重力异常数据进行二维EMD分解,得到3组重力异常数据,分别为第一级固有模态函数(IMF1),第二级固有模态函数(IMF2)和剩余分量(residue)。
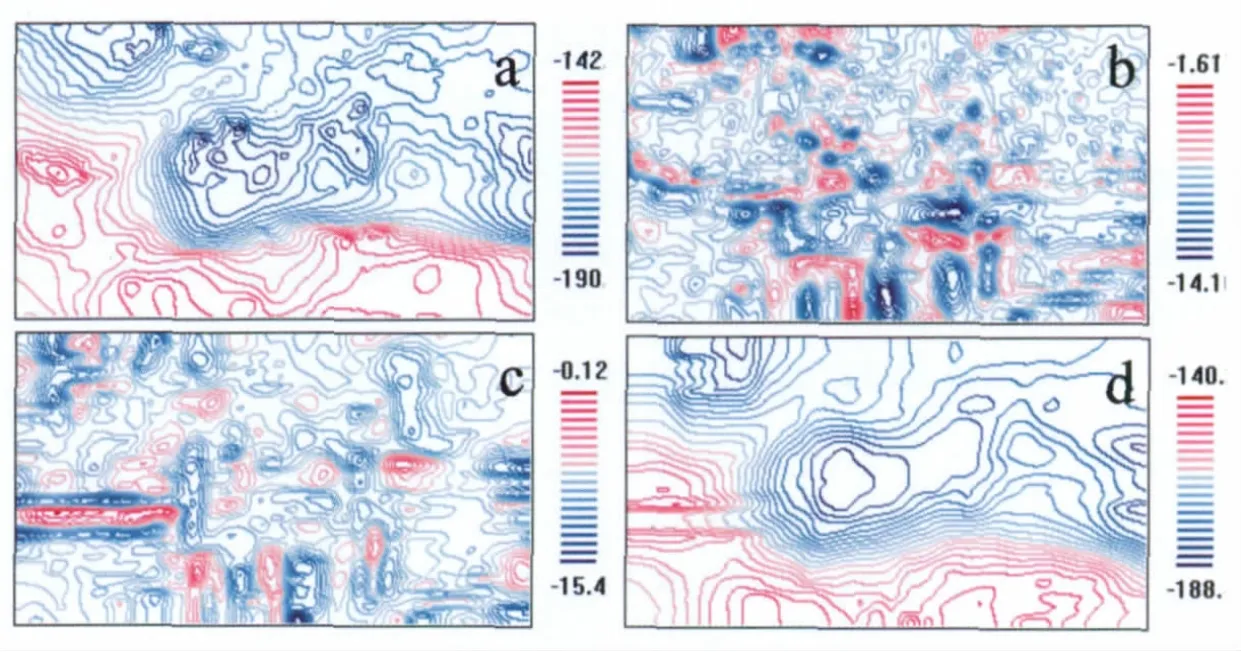
图5 个旧地区重力异常分解结果图Fig.5 EDM decoposition diagram of gravity data for Gejiu area
在MORPAS中得到这3组重力异常数据的等值线图,如图5所示。其中,图5a为研究区重力异常等值线图,图5b,c和d分别为研究区第一级局部重力异常等值线图、第二级局部重力异常等值线图和区域重力异常等值线图。在图6a中,有2条主要的断裂带(以红色线条表示)直接影响着异常的分布,分别是NW向的红河断裂和SN向的小江断裂,出露的岩体主要分布在个旧以南的哀牢山地区和个旧以西的石屏一带(以绿色线条表示)。为说明图5b,c和d异常等值线图所代表的实际物理意义,在Map GIS中,对这3组重力异常等值线图与研究区出露岩体和2条主要断裂进行叠加,得到3幅叠加图(图6b、图6c和图6d)。从这3幅图可以看出:①在图6b和图6c中,大部分出露的花岗岩落在短轴状或椭圆状等值线内,这与浅部花岗岩产生小面积短轴状或椭圆状等值线相符合,反映浅部地质信息,根据类似等值线形状可以推测隐伏岩体;②在图6d中,异常等值线在南、北两侧存在明显差异,这符合个旧地区因红河断裂引起的异常差异;另外,在图6d中,出现由EW向展布的同心状个旧重力低和蒙自重力低,且南部有近EW向展布的重力梯级带,个旧岩体东边有近弧形的梯级带,这与研究区的地质情况相符(图6a),反映出深部的地质构造特征。
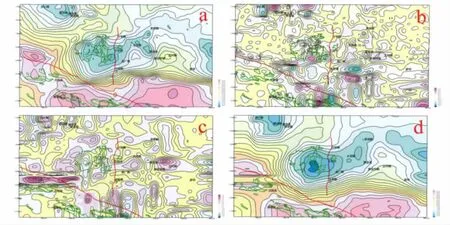
图6 个旧地区重力异常二维EMD数据处理等值线图Fig.6 The EMD-processed gravity contour map of Gejiu area
4 结论
通过研究二维EMD方法在云南个旧地区物化探数据处理中的应用,证实了二维EMD方法处理物化探数据的可行性。二维EMD分解得到的所有分量都具有实际地质意义,有效地分离了物化探异常,它将是一种新的物化探数据处理方法。
本文首次将BEMD用于处理物化探数据,初步分析取得了一定的效果,但尚属应用研究的初级阶段。今后还需进一步的对二维EMD方法的分解方式进行研究,充分改善端点效应及二维EMD方法对分解效果的影响,使物化探数据的处理取得更佳的应用效果。
[1] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstastinary time series analysis[J].Proc Roy Soc London Ser A,1998,454:903-995.
[2] Nunes J C,Bouaoune Y,Delechelle E,et al.Image analysis by bidimensional empirical mode decomposition[J].Image and Vision Computing,2003,21(12):1019-1026.
[3] 沈滨,崔峰,彭思龙.二维EMD的纹理分析及图像瞬时频率估计[J].计算机辅助设计与图形学学报,2005,17(10):2346-2352.
[4] 盖强,殷福亮.二维Hilbert-Huang变换的分解方法研究[J].电子与信息学报,2006,28(4):610-613.
[5] 宋平舰,张杰.二维经验模分解在海洋遥感图像信息分离中的应用[J].高技术通讯,2001(9):62-67.
[6] 刘忠轩,彭思龙.方向EMD分解与其在纹理分割中的应用[J].中国科学E辑,2005,35(2):113-123.
[7] 肖凡.基于RAGA的PPC模型在个旧化探资料处理中的应用研究[D].武汉:中国地质大学(武汉),2008.
[8] 熊光楚,石盛滕.个旧锡矿区物理-地质模型及应用效果[J].地质论评,1994,40(1):19-27.
