基于核基因组标记的群体遗传学研究中的数学分析方法＊

包振民，王明玲，李 艳，张玲玲，胡晓丽，黄晓婷，胡景杰，王 师

（中国海洋大学海洋生命学院海洋生物遗传育种教育部重点实验室，山东青岛266003）

基于核基因组标记的群体遗传学研究中的数学分析方法＊

包振民，王明玲，李 艳，张玲玲，胡晓丽，黄晓婷，胡景杰，王 师

（中国海洋大学海洋生命学院海洋生物遗传育种教育部重点实验室，山东青岛266003）

近些年来，各种数学分析方法被广泛的应用于群体遗传学的研究中。然而，对这些数学分析方法的应用缺乏统一的认识，某些研究甚至存在着误用、乱用等现象。对近些年来基于核基因组标记的群体遗传学研究中主要采用的数学分析方法进行了系统的归纳整理，明晰了它们的适用条件和范围。同时，也综述了显性分子标记中对隐性等位基因频率估算的研究进展以及常用的群体遗传学分析软件包含的主要数学分析方法，对合理应用这些参数和软件进行群体遗传学分析具有指导意义。

群体；分子标记；数学分析方法；隐性等位基因频率

生物群体内或群体间的动态变化规律是群体遗传学研究的核心内容。传统的群体遗传学研究主要采用野外调查和形态标记等手段，但往往难以克服野外调查周期长、分辨率有限及环境条件难以控制等问题。分子标记技术的出现，有效地克服了传统研究手段的缺陷，迅速成为群体遗传学研究的主要手段。随着群体遗传学研究的深入，众多针对分子标记的数学分析方法被发展出来以用于解析生物群体内或群体间的动态变化规律，例如等位基因数目（Number of alleles）［1］、杂合度（Heterozygosity）［2］、有效群体大小（Effective population size）［3－10］、Hardy－Weinberg平衡（Hardy－Weinberg Equilibrium）［11－12］、遗传距离（Genetic distance）［13－16］和基因流（Gene flow）［17－23］等。对这些数学分析方法的应用，国内研究尚缺乏统一性认识，某些研究甚至存在着误用、乱用等现象。但迄今为止，尚未见有研究对这些数学分析方法进行系统的归纳整理。

本文综述了近年来基于核基因组标记的群体遗传学研究中主要采用的数学分析方法，重点对这些方法进行系统的归纳整理，以明晰它们的适用条件和范围。同时，也对显性分子标记中隐性等位基因频率的估算的研究进展以及常用的群体遗传学分析软件包含的主要数学分析方法进行了归纳整理。

1 群体遗传学分析中常用的数学分析方法的归类与解析

对群体遗传学分析中常用的数学分析方法的归类见表1。首先，根据数学分析方法分析的是群体的遗传规律还是群体的变异规律，将其分为两大类。其次，将分析群体变异规律的数学分析方法进一步分为群体内遗传多样性和群体间遗传分化2类。

表1 群体遗传学分析中常用的数学分析方法Table 1 Mathematic analysis methods for the research of population genetics

1.1 解析群体遗传规律的数学分析方法

1.1.1 Hardy－Weinberg平衡 Hardy－Weinberg定律是1908年由英国学者Hardy和德国学者Weinberg各自独立提出的关于群体内基因频率和基因型频率变化的规律。其中心内容是：在随机交配的大群体内，若没有突变、选择、漂变或迁移因素的作用，则基因频率和基因型频率将在世代间保持恒定。符合上述条件的群体即为H－W平衡群体。

1.1.1.1 H－W平衡群体的检验 H－W平衡群体的检验通常主要采用卡方检验（χ2test）、似然比检验（Likelihood ratio test）或精确检验（Exact test）来判别实测的基因型频率与理论推断数值是否相符合，从而确定该群体是否处于平衡状态。卡方检验和似然比检验为过去的研究中所主要采用，但由于经常存在1个或多个基因型有低的期望值，而使这2种检验可能会得出不可靠的结果。1个常用的解决方法就是采用合并策略，如：分成纯合子和杂合子。但合并的策略会导致某些信息的丢失。基于这个原因，精确检验被认为更为适合于检验H－W平衡群体［22］。对1个位点存在2种以上等位形式的情况，Guo和Thompson［23］提出了2个方法应用于精确检验：蒙特卡罗法（Monte Carlo method）和马尔科夫链法（Markov Chain method）。通常，蒙特卡罗法对小数据集（每位点含少于50～75个观测值）运算速度更快；而马尔科夫链法对大数据集可得到更好的运算结果。

1.1.1.2 Wright固定指数 Wright固定指数（F）用于检验群体实际观测杂合度与理论期望杂合度的偏离程度及原因。其计算公式为［24］：

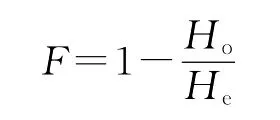
式中：Ho为实际观测杂合度，He为理论期望杂合度。当F＝0时，群体符合H－W平衡；当F＜0时，群体实际杂合度超过期望杂合度；当F＞0时，群体实际杂合度低于期望杂合度。

1.1.2 有效群体大小 在实际群体内，并不是所有个体都能同等地参加繁殖过程。实际群体所具有的相当于理想群体繁育个体数目的个体数称为有效群体大小。预测实际群体的有效群体大小主要应用于群体遗传保护方面（如种质资源库的建立、群体衰退的鉴定等）。直接估测有效群体大小是非常困难的，尤其是对于自然种群，因为这涉及一些参数的测定，如不同个体存活力和繁殖率的测定等。为了解决这个问题，一些间接估测有效种群大小的方法已被发展。这些方法主要基于：

①等位基因频率的时序变化

其基本原理：通过分析群体经过t世代后等位基因频率的时序变化，来计算有效群体大小。其计算公式为［1］：

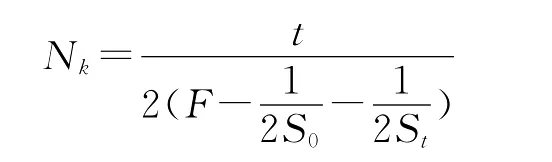
式中：t为世代数目；S0和St分别为0世代和t世代取样个体数目；F为Fk相对各位点的平均值。Fk可由下面3式之一得出：

尽管Waples和Teel［5］通过修正使得2次取样间隔可在一代之内，但该方法仍需要2次取样样品。

②连锁不平衡

其基本原理：通过分析群体连锁不平衡的情况，来计算有效群体大小。其计算公式为［6］：

式中：S为样本大小；p、q分别为位点1等位基因A和位点2等位基因B的频率；D为连锁不平衡的度量值。该方法缺点：当样品的分析位点数目较少时，易产生较大误差。

③杂合子过剩

其基本原理：基于小数目的亲本产生F1子代，会出现暂时的杂合子过剩现象，根据这种现象即可计算建立者群体大小。其计算公式为［7］：

式中：Ho为实际观测杂合度，He为理论期望杂合度。

④等位基因数目的减少

其基本原理：刚经历过瓶颈（Bottleneck）的群体，与经历瓶颈前群体（即Control群体）相比，其等位基因数目会相应地减少，根据减少的等位基因数目，即可推断出群体的有效大小。其计算公式为［8］：

式中：C和k可由SAS软件nlin过程进行估算。

1.1.3 连锁不平衡 群体中2个或2个以上位点等位基因非随机关联现象称为连锁不平衡或配子相不平衡。产生连锁不平衡的原因主要有：①被考察的群体来源于具有等位基因A、a和B、b不同频率的2个群体，这2个亚群体混合的时间不足以产生完全的随机化；②位于同一条染色体上的2个突变体距离较近，二者之间未经足够的世代，通过重组来分离；③某些基因座的等位基因组合有选择优势而维持较高频率。

衡量位点间连锁不平衡的统计量有很多，最常见的是r2和D′。二者的基本组分是度量观测单倍型频率与期望单倍型频率的差异（Dab）。

式中：πAB为单倍型AB的频率；πA、πB为位点A和B的频率

①r2

其计算公式为［25］：

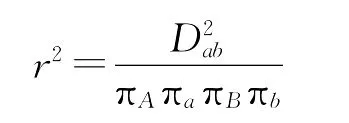
②D′

其计算公式为［26］：

这里，r2着重的是对突变和重组的估计；D′着重的仅是对重组的估计，因而对重组差异的估计更为精确［27］。但是在小样品或低等位基因频率时，r2和D′的估计都不甚理想。

1.2 解析群体变异规律的数学分析方法

1.2.1 群体内遗传多样性

1.2.1.1 等位基因数目与有效等位基因数目 等位基

因数目即群体内某位点全部的等位基因总数，其是衡量群体内遗传多样性的一个最基本指标。有效等位基因数目（Ae）即可维持在有限群体中的等位基因数目［9］。

式中：Pi为等位基因i的频率。相比而言，有效等位基因数目在衡量群体内遗传多样性方面有着更为广泛的应用。

1.2.1.2 多态位点比率 多态位点比率即具有2个或2个以上等位基因的位点占全部位点的百分率。它是1个相对笼统的衡量群体内遗传多样性的指标。通常以群体内某位点最高等位基因频率小于某个域值时，作为多态性位点的判断标准。如对同工酶来说，域值为0.95；而对微卫星而言，域值定为0.99比较合适。

1.2.1.3 香农多样性指数 香农多样性指数主要基于数学角度同时考虑等位基因数目与丰度来衡量群体的遗传多样性，其应用较为广泛。其公式为［28］：

Sheldon［29］修正的香农多样性指数可以消除不同群体间样本大小对多样性指数的影响。其公式为：

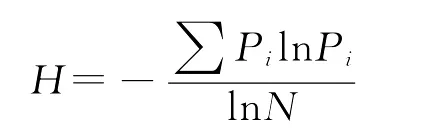
以上式中：Pi为等位基因i在群体中出现的频率；N为群体样本大小。

1.2.1.4 杂合度 杂合度即群体内杂合子个体数占全部个体数的比例，主要基于遗传角度来衡量群体内遗传多样性水平。对所有位点的杂合度求平均即为观测杂合度（Ho）；期望杂合度（He）是基于等位基因频率从Hardy－Weinberg平衡公式计算得到。平均期望杂合度又称为Nei基因多样度（He）。其计算公式为［10］：

式中：n为位点总数；hi为第i个位点的杂合度，xj为第j个等位基因的频率。

观测杂合度在应用于衡量群体内遗传多样性时，有时存在问题（如：对某个标记位点，若群体所有个体的基因型都为AA或aa，则Ho＝0，但He却不为0），所以，期望杂合度应用得更为广泛。但期望杂合度的计算需假设群体符合H－W平衡，若群体严重偏离HW平衡，则须采用其它指标（如香农多样性指数）来衡量群体内遗传多样性。

1.2.2 群体间遗传分化

1.2.2.1 FST和GSTFST又称为近交系数，是进行群体间遗传分化概括分析最常用的方法之一。FST指示特定基因座位在群体间的分化程度［30］。FST的计算主要采用如下2种方法：

①基于基因频率方差

其计算公式为：

式中：p为某等位基因在整个群体中的频率，其方差为Var（p）

②基于杂合度

其计算公式为：

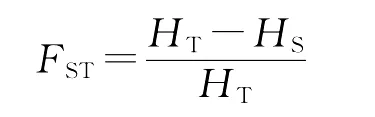
式中：HS为多个亚群体内期望杂合度的平均值；HT为整个群体的期望杂合度。

但Wright的FST在实际应用中存在一些问题，如该模型是由共显性双等位基因位点推导而来、等级结构较少等。因此不同学者又在Wright的FST基础之上建立或完善了与之相关的各种参数。

当分析群体间在许多基因座位上的平均分化程度时，可以计算GST［31－32］。其计算公式为：

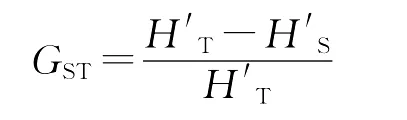
式中：H′T为整个群体的平均杂合度；H′S为亚群体内平均杂合度。

1.2.2.2 AMOVA Excoffier等［33］发展了1种分子方差分析（Analysis of Molecular Variance，AMOVA）方法。该方法通过估计单倍型或基因型之间的进化距离，进行遗传变异的等级剖分，并提出了与FST类似的ΦST来度量亚群体间的分化。AMOVA方法适用于所有类型的遗传学数据，可以在不需要假设的情况下直接对显性标记数据进行分析，加上相应分析软件WINAMOVA［34］的应用，使得各种单倍型和显性标记数据在群体遗传结构研究中得到了广泛的应用。

该方法的基本原理［35］：假定在1组或多组群体中，第k组第j个群体的第i个单倍型（或基因型）的xijk频率向量可用一个线型可加模型假定：

式中：x是在整个研究中xijk的未知期望值，a是组（或地区）的效应，b是群体的效应，c是群体内单倍型（或基因型）的效应。这3个效应具可加性、随机性、独立性，且分别具方差通过等级剖分计算组间、组内／群体间、群体内方差组分的期望值，分别计算各个等级对总遗传变异的贡献率。相应的ΦST由以下公式计算：

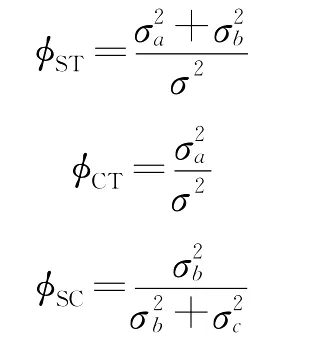
式中：ΦST、ΦCT、ΦSC分别反映群体间、组间、群体内的遗传分化。

1.2.2.3遗传距离 遗传距离是用来对群体间遗传分化程度进行量化分析的指标。目前，关于遗传距离的统计方法众多，这里主要介绍较为常用的Nei遗传距离（基于基因频率）和Jaccard遗传距离（基于基因型频率），以及基于逐步突变模型的ASD和（δu）2。

①Nei遗传距离

Nei遗传距离是基于无限基因突变模型的应用最广泛的距离测度。该模型假定每次突变产生1种新的当前种群不存在的等位基因。这就意味着如果2个等位基因相同，则没有突变发生；如果2个等位基因不同，则至少发生1次突变，但不清楚这种情况下突变发生的具体次数。突变的分布服从泊松（Poisson）分布。

如果基因的替换速率对于所有位点都相同，其表达式为：

式中：p为某位点某等位基因在群体x中的频率；q为某位点某等位基因在群体y中的频率。

如果基因替换的速率对于所有位点并不相同，D会过低估计每个位点基因替换的累积数目，则一个更合适的遗传距离的测度由下式给出［11］：

式中：J′xy、J′xx和J′yy分别为Jxy、Jxx和Jyy的几何平均值。

②Jaccard遗传距离

Jaccard遗传距离是基于基因型频率的常用距离测度，适合于显性遗传标记数据的计算。其表达式为［12］：

式中：Axy为x和y群体具有相同基因型的数目；Bxy为x和y群体全部基因型的总数。

③ASD和（δu）2

ASD和（δu）2均为基于逐步突变模型的距离测度。该模型假定突变是逐步发生的，主要针对同功酶电荷差异或微卫星重复次数差异进行遗传距离的计算。

ASD的计算公式为［13］：

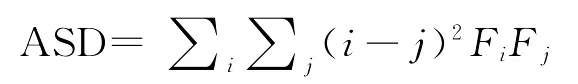
式中：Fi、Fj分别为群体A中第i个等位基因频率和群体B中第j个等位基因频率。在逐步突变模型下，ASD与时间成线性函数关系。但其缺陷是未考虑距离的方差。

（δu）2的计算公式为［14］：

式中：μA、μB为群体A和群体B等位基因大小的均数。（δu）2从ASD发展而来，更适合于测度亲缘关系较远的群体之间的遗传距离。

1.2.2.4 基因流 当一些个体从1个群体迁移至另1个群体时，就会产生基因流动，即基因流。基因流是影响群体内部和群体之间遗传变异程度的重要因素。对基因流的研究，近些年来越来越受到重视。它对群体遗传学、进化生物学、保护遗传学、生态学有着极其重要的作用。对基因流的研究主要分为直接方法和间接方法。传统上，主要采用直接方法（如标记－重捕法等）估测基因流的大小，但其精确性有很大局限性，而且对大的群体应用非常困难。随着分子标记技术的发展，对基因流的研究逐渐向分子水平过渡，目前，大部分研究主要采用间接方法进行群体间基因流的研究。

①岛屿模型中的Nm和距离隔离模型中的Nb

岛屿模型是Wright［15］提出的用于描述群体遗传结构的经典模型。该模型的基本思想是假设1个群体分化为无限多个亚群体，亚群体在空间呈离散分布，每个亚群体接受一小部分来自整个群体的迁移个体。迁移率与迁移基因频率在任一世代内假设为常数。岛屿模型中的Nm为每代迁入的有效个体数，即基因流的估计值。其计算公式为：

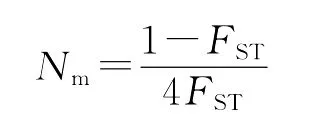
一般来讲，Nm的值远小于1时将导致较强的种群分化，而Nm值大于4的群体可以作为1个单一随机交配群体。

距离隔离模型由Wright［16－17］提出。与岛屿模型情况相反，距离隔离模型中的群体在空间上呈连续分布。由于有限的短距离基因迁移（即个体间交配仅局限于小范围内进行），远距离分开的不同个体群由于有限距离的基因迁移而产生遗传分化。该模型的1个重要参数就是邻近群体大小（Nb），它被定义为一定范围内能随机交配的个体数量，其作用与岛屿模型中的Nm一样。其计算公式为：

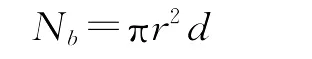
式中：r为个体间能随机交配范围的半径；d为群体密度。

利用Nm和Nb推断基因流的缺点是：限制条件非常多，对现实群体而言，一些条件难以满足。

②共祖检验

共祖检验主要是通过追踪个体的祖先谱系关系，来推断个体是否为迁移个体或迁移个体后代，可获得群体间长时间的基因流的估计值。该检验放宽了一些限制条件（如短期内群体的扩张，非交互式迁移等）。但仍然要求群体有恒定的大小或连续4 Ne代确定的扩张方向［18］。

③指定检验

指定检验根据个体的基因型，将个体指定到其来源群体（该基因型可能发生的最大概率的群体）中去。由于指定检验主要依据短期内迁移个体或其后代的基因型存在暂时的不平衡现象，所以该方法只能推断短期内（一般在几代之内）的基因流估计值。目前，已有一些统计软件可进行指定检验，如：Pritchard等［19］开发的Structure和Schneider等［20］开发的Arlequin。

④Bayesian推断

Wilson和Rannala［21］根据Bayesian理论提出的利用个体多位点基因型来估算群体间新近的迁移率的新方法。相比而言，这一方法需要更少得假设条件，甚至可应用于非H－W平衡的群体。目前，该方法已可由相应的统计软件Bayes Ass来实现。

1.2.2.5 空间自相关分析 空间自相关分析是1种统计方法，被广泛应用于描述群体遗传变异的空间格局。主要应用于在空间呈连续或团块分布的群体。空间自相关分析的第一步是将取样点标定在图上，作成一个取样点分布平面。然后，根据不同距离层次，在平面相关点之间建立关联（盖比列关联Gabriel connection或最近邻体关联Nearest neighbor connection），确定不同取样点对的权。常采用二元加权系统，即关联的取样点i和j之间Wij＝Wji＝1，不关联的取样点i和j之间Wij＝Wji＝0。构建完成关联矩阵W后，即可计算空间自相关分析系数。空间自相关分析系数主要有如下几种：

①Moran系数I

其计算公式为［36］：

式中：N是样品数目；Ai和Aj是样品i和j的等位基因频率值；珡A是所有样品等位基因频率的平均值；Wij是给定距离层次上关联矩阵W的元素。I值介于－1和1之间。

②Geary系数C

其计算公式为［37］：

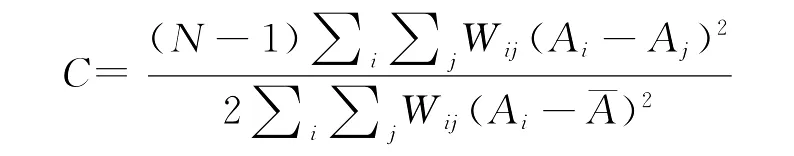
C值介于0和2之间。一般认为，Moran系数I可以提供更为整体性的指标；Geary系数C对邻近关联对的差异更为敏感。

③Mentel系数Z

其计算公式为［38］：

式中：Nij为样品i和j间的遗传距离。Z值介于0和1之间，主要用于检测样品间遗传距离和地理距离间的相关性。

上述几种自相关分析系数的方法在遇到遗传障碍出现，不同地理区域之间有明显差异的情况时，分析会出错［39］。因此，Franz等［40］提出用Monmonier最大化差异运算法则来确定地理模型的边界，从而进一步将遗传变异跟地理模型做关联分析。

2 显性分子标记中隐性等位基因频率的估算

在众多的分子标记中，RAPD和AFLP等显性标记，由于具有无需预先知道基因组信息、可在短时间内完成大量样品的分析工作等优点，在许多研究领域获得了广泛的应用。但由于它们是显性标记，不能区分纯合子和杂合子，在基因频率的统计上存在着很大的困难。目前，对显性分子标记中隐性等位基因频率的估算主要有以下几种方法：

①平方根法

其计算公式为［41］：

式中：m为隐性纯合体的个体数；n为个体总数。平方根法是过去较为常用的方法，此法要求群体符合H－W平衡且易产生较大偏差。

②LM法

其计算公式为［42］：

LM法也要求符合H－W平衡，且对当m≤3时的位点不予计算，因而，该法受样本大小的影响很大，偏向于选择隐性等位基因频率高的位点，会造成有偏估计。

③FIS值法

在群体偏离H－W的情况下，Chong等［43］提出了1个估测隐性等位基因频率的方法，即利用对同一群体进行的共显性标记分析（同工酶或SSR）计算得到的FIS值来估测隐性等位基因频率。解如下方程，可得q′：

式中：FIS为根据共显性标记计算得到的该群体的固定指数。

④Bayesian法

Bayesian法是Zhivotovsky［44］基于Bayesian理论提出的估算隐性等位基因频率的新方法。

在群体符合H－W平衡的条件下，其计算公式为：

式中：Pr（m｜q）为在隐性等位基因频率为q的前提下，样品中含有m个隐性纯合体的概率；Pr（q）为样品隐性等位基因频率为q的概率。

在群体偏离H－W非平衡的条件下，其计算公式为：

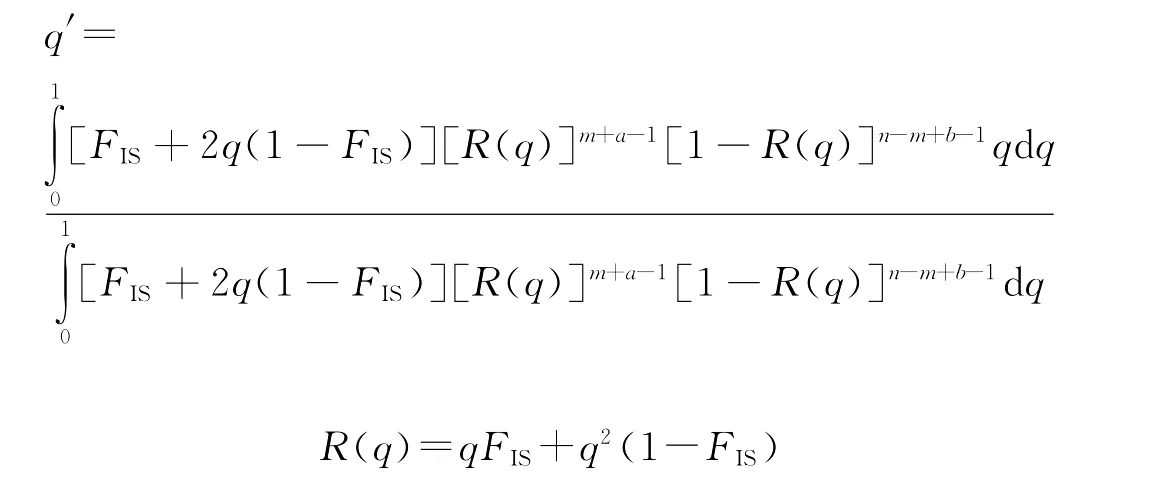
与前述方法相比，Bayesian法可获得更为准确的隐性等位基因频率的估计值。

3 群体遗传学分析中常用的数学分析软件

目前，有关群体遗传学分析的软件数目众多。以上介绍的数学分析方法几乎都可由软件自动实现。群体遗传学分析中常用的数学分析软件包有：TFPGA、Arlequin、GDA、GENEPOP、Gene Strut、POPGENE、等。对这些常用的分析软件所包含的主要数学分析方法的总结见表2。

表2 常用的群体遗传学分析软件及其包含的主要数学分析方法一览Table 2 Common software of population genetics and mathematic analysis methods included

续表2

4 结语

目前，国内已开展了大量的利用分子标记技术进行群体遗传多样性和群体遗传结构分析的研究工作，然而如何正确使用相关数学分析方法，合理地分析和处理数据，仍是值得注意的问题。本文对群体遗传学分析中常用的数学分析方法、显性分子标记中隐性等位基因频率的估算方法以及常用的群体遗传分析软件进行了系统的归纳整理，明确了常用遗传参数的适用条件和范围，对合理地应用这些遗传参数进行群体遗传学分析具有指导意义。

［1］ Kimuraz M，Crow J F.The number of alleles that can be maintained in a finite population［J］.Genetics，1964，49：725－738.

［2］ Nei M.Molecular Population Genetics and Evolution［M］.Amsterdam：North－Holland Publishing Company，1975.

［3］ Waples R S.A generalized approach of estimating effective population size from temporal changes in allelic frequency［J］.Genetics，1989，121：379－391.

［4］ Nei M，Tajima F.Genetic drift and estimation of effective population size［J］.Genetics，1981，98：625－640.

［5］ Pollak E.A new method for estimating the effective population size from allele frequency changes［J］.Genetics，1983，104：531－548.

［6］ Krimbas C B，Tsakas S.The genetics of Dacus oleae.V.changes of esterase polymorphism in a natural population following insecticide control－selection or drift［J］.Evolution，1971，25：454－460.

［7］ Waples R S，Teel D J.Conservation genetics of Pacific Salmon I.Temporal changes in allele frequency［J］.Conservation Biology，1990，4：144－156.

［8］ Waples R S.Genetic methods for estimating the effective size of Cetacean populations.1991：279－300 in Genetic Ecology of Whales and Dolphins［M］.Hoelzel A R ed.London：Special Issue 13.International Whale Commission，1991.

［9］ Pudovkin A I，Zaykin D V，Hedgecock D.On the potential for estimating the effective number of breeders from heterozygote－excess in progeny［J］.Genetics，1996，144：383－387.

［10］ Launey S，Barre M，Gerard A，et al.Population bottleneck and effective size in Bonamia ostreae－resistant populations of Ostrea edulis as inferred by microsatellite markers［J］.Genet Res Camb，2001，78：259－270.

［11］ Haldane J B S.An exact test for randomness of mating［J］.Journal of Genetics，1954，52：631－635.

［12］ Guo S W，Thompson E A.Performing the exact test of Hardy－Weinberg proportion for multiple alleles［J］.Biometrics，1992，48：361－372.

［13］ Nei M.Interspecific gene differences and evolutionary time estimated from electropho retic data on protein identity［J］.Amer Natur，1971，105：385－398.

［14］ Jaccard P.Nouvelles recherches sur la distribution florale［J］.Bull Soc Vaud Sci Nat，1908，44：223－270.

［15］ Goldstein D B，Ruiz Linares A，Cavalli－Sforza L L，et al.An E－valuation of Genetic Distances for Use with Microsatellite Loci［J］.Genetics，1995，139：463－471.

［16］ Goldstein D B，Linares A R，Cavalli－Sforza L L，et al.Genetic absolute dating based on microsatellites and the origin of modern humans［J］.Proc Natl Acad Sci，1995，92：6723－6727.

［17］ Wright S.Evolution in Mendelian populations［J］.Genetics，1931，16：97－159.

［18］ Wright S.Breeding structure of populations in realtion to speciation［J］.Ammican Naturalist，1940，74：232－248.

［19］ Wright S.Isolation by distance［J］.Genetics，1943，28：114－138.

［20］ Kingman J F C.On the genealogy of large populations［J］.J Appl Prob，1982，19A（Sup）：27－43.

［21］ Pritchard J K，Stephens M，Donnelly P J.Inference of population structure using multilocus genotype data［J］.Genetics，2000，155：945－959.

［22］ Schneider S，Roessli D，Excoffier L.Arlequin：a software for population genetics data analysis［CP／DK］.Genetics and Biometry Lab，Dept.of Anthropology，Switzerland：University of Geneva，2000.

［23］ Wilson G A，Rannala B.Bayesian inference of recent migration rates using multilocus genotypes［J］.Genetics，2003，163：1177－1191.

［24］ Wright S.The interpretation of population structure by F－statistics with special regard to systems of mating［J］.Evolution，1965，19：395－420.

［25］ Hill W G，Robertson A.Linkage disequilibrium in finite populations［J］.Theor Appl Genet，1968，38：226－231.

［26］ Lewontin R C.The interaction of selection and linkage.I.General considerations；heterotic models［J］.Genetics，1964，49：49－67.

［27］ Flint－Garcia S A，Thornsberry J M，Buckler E S.IV structure of linkage disequilibrium in plants［J］.Annu Rev Plant Biol，2003，54：357－374.

［28］ Shannon C E，Weaver W.The mathematical theory of communication［M］.Urbana：University of Illinois at Urbana－champaign，1949.

［29］ Sheldon A L.Equitability indices：dependence on the species count［J］.Ecology，1969，50：466－467.

［30］ Wright S.The genetical structure of populations［J］.Ann Eugen，1951，15：323－354.

［31］ Nei M.Genetic distance between populations［J］.Amer Natur，1972，106：283－292.

［32］ Nei M.Analysis of gene diversity in subdivided populations［J］.Proc Natl Acad Sci USA，1973，70：3321－3323.

［33］ Excoffier L，Smouse P E，Quattro J M.Analysis of molecular variance inferred from metric distances among DNA haplotypes：applications to human mitochondrial DNA restriction data［J］.Genetics，1992，131：479－491.

［34］ Excoffier L.Analysis of molecular variance（AMOVA）version 1.55［CP／DK］.Genetics and Biometry Laboratory，Switzerland：University of Geneva，1993.

［35］ 张富民，葛颂.群体遗传学研究中的数据处理方法I.RAPD数据的AMOVA分析［J］.生物多样性，2002，10：438－444.

［36］ Moran P A P.Notes on continuous stochastic phenomena［J］.Biometrika，1950，37：17－23.

［37］ Geary R C.The contiguity ratio and statistical mapping［J］.The Incorporated Statistician，1954，5：115－145.

［38］ Manly B F J.Randomization，bootstrap and Monte Carlo methods in biology［M］.London：Chapman ＆Hall，1997.

［39］ Manni F，Guerard E，Heyer E.Geographic Patterns of（Genetic，Morphologic，Linguistic）Variation［J］.Human Biology，2004，76：173－190.

［40］ Monmonier M.Maximum－difference barriers：An alternative numerical regionalization method［J］.Geogr Anal，1973，3：245－261.

［41］ Clark A G，Lanigan C M S.Prospects for estimating nucleotide divergence with RAPDs［J］.Mol Biol Evol，1993，10：1096－1111.

［42］ Lynch M，Milligan B G.Analysis of population genetic structure with RAPD markers［J］.Mol Ecol，1994，3：91－99.

［43］ Chong D K，Yang R C，Yeh F C.Nucleotide divergence between populations of trembling aspen（Populus tremuloides）estimated with RAPDs［J］.Curr Genet，1994，26：374－376.

［44］ Zhivotovsky L A.Estimating population structure in diploids with multilocus dominant DNA markers［J］.Molecular Ecology，1999，8：907－913.

Mathematical Analysis Methods Used in Population Genetics Studies Based on Nuclear Genome Markers

BAO Zhen－Min，WANG Ming－Ling，LI Yan，ZHANG Ling－Ling，HU Xiao－Li，HUANG Xiao－Ting，HU Jing－Jie，WANG Shi
（The Key Laboratory of Marine Genetics and Breeding，Ministry of Education，College of Marine Life Sciences，Ocean University of China，Qingdao 266003，China）

In recent years，a variety of mathematical analysis methods have been widely used in population genetics studies.However，lack of a unified undestanding of the application of these methods has led to misuse and abuse them in some instances.In this study，we reviewed major mathematical analysis methods recently used in population genetics based on nuclear genome markers.These methods were classified and their applicable conditions and limitations were shown，which is essential to apply them correctly.Moreover，we also reviewed recent progress of estimating recessive allele frequency and major mathematical analysis methods included in popular software packages for population genetic analyses，which is instructive for researchers to make appropriate use of these methods or softwares.

population；molecular marker；mathematical analysis method；recessive allele frequency

Q347

A

1672－5174（2011）11－048－09

国家高技术研究发展计划项目（2006AA10A408）；公益性行业科研专项（nyhyzx07－047）；现代农业产业技术体系建设专项资助

2010－04－26；

2011－05－19

包振民（1961－），男，教授，博导，主要从事海洋贝类分子遗传与育种的研究。E－mail：zmbao＠ouc.edu.cn

责任编辑 朱宝象