沉积物粒度参数和频率曲线对粒级划分的响应*

付莉莉,冯秀丽,杨旭辉

(中国海洋大学海洋地球科学学院,山东青岛266100)

沉积物粒度参数和频率曲线对粒级划分的响应*

付莉莉,冯秀丽,杨旭辉

(中国海洋大学海洋地球科学学院,山东青岛266100)

以Φ、Φ/2、Φ/4为粒级间距,分别采用Folk-Ward图解法和Mc Manus矩法计算了粉砂质砂、黏土质粉砂、砂-粉砂-黏土等3类沉积物共136个底质样品的粒度参数,并引用统计学中的单因素方差分析法对每一类沉积物的每一个粒度参数进行分间距计算结果对比。结果表明,各类沉积物在各种计算方法中粒级划分对粒度参数表征粒度分布特征均不构成影响。但粒度频率曲线形态随粒级间距的不同会有变化,同一粒径所对应的频率值在不同粒级间距下有较大差异。因此,在进行动力条件和沉积环境等研究时,必须对粒级间距在粒度分析中的影响给予足够重视。在进行粒度分析时,如果只求粒度参数,采用Φ间距即可,这样可以减小工作量;如果研究沉积环境,建议采用Φ/4间距。

粒级划分;粒度参数;图解法;矩法;方差分析法;粒度频率曲线

对沉积物样品进行粒度分析、获取其粒度特征是地学研究的经常步骤。沉积物的粒度特征使用粒度参数来表征。目前广泛使用的粒度参数包括平均粒径、分选系数、偏态和峰态等。长期以来,粒度参数在研究沉积环境、沉积动力学和工程地质等方面都有广泛应用,也有学者将粒度分析用于探讨河口地区的絮凝机理。蒲晓强[4]等对南黄海柱状样沉积物进行了粒度参数求解,研究了南黄海不同典型海域沉积物的粒度特征及其对沉积环境和水动力条件的响应特征;张富元[5]等对南海东部海域沉积物进行了粒度分析,探讨了沉积物的粒度分布特征、运移方式和沉积环境;陈敬安[6]等对洱海和程海的现代沉积物粒度进行了研究,揭示了沉积物粒度在不同时间尺度、不同时间分辨率的研究中具有不同的环境指示意义;孙千里[7]等通过对岱海沉积物粒度频率曲线的分析,讨论了湖泊的几种可能沉积作用,区分了正常流水沉积与极端条件下风力作用以及水流与风力作用混合沉积,揭示了沉积时的古环境特征;蒋忠信[8]通过对几种成因类型砂的分选系数σ与中值粒径M d的沿程变化及相互关系进行分析,为推论沉积环境提供依据;Juan JoséKasper-Zubillaga[9]等通过对墨西哥西北部索诺拉州粒度分布参数结构的研究,对沙漠砂和海岸沙丘砂进行了辨别;G.De Falco[10]对西地中海撒丁岛泳滩及大陆架沉积物样品进行粒度分布、组成分析,并对生物碎屑进行对比,以确定沙滩沉积物和泥沙的来源;Gao&Collins[11]认为沉积物净输运方向与粒度参数的空间变化(粒径趋势)相联系,提出粒径趋势分析模型,促进了粒度特征研究乃至颗粒态物质动力学的进步;左书华[12]、刘永学[13]、程鹏[14]等分别对南汇嘴、江苏省细颗粒潮滩区和北黄海西部海底的沉积物进行了粒度分布特征分析,并利用Gao&Collins沉积物趋势分析法探讨了沉积物的输运趋势;李安春[15]等利用悬浮体絮凝现场粒径资料,结合温度、盐度及悬浮体总量等对伊姆斯–道拉德河口的悬浮体絮凝过程及其控制因素进行了研究;夏福兴[16]等使用带电子探针的扫描电子显微镜分析和测定了长江口悬浮颗粒样品,根据长江口的物理化学环境和悬浮颗粒的性质,探讨了有机絮凝体的形成机理,解释了长江口悬浮颗粒有机絮凝体的形成。

计算粒度参数的方法有多种,当前广泛使用的主要有图解法和数理统计(以下称矩法)2类。图解法是通过在粒度累积曲线上选择几个具有一定意义或代表性的点,利用简单的计算程序求得一系列参数[17]。因其计算简便而被广泛采用。矩法则是将样品的平均粒径、分选系数、偏态和峰态等分别定义为粒度分布的一阶矩、二阶矩、三阶矩和四阶矩函数,其计算公式有多个[17]。已有不少学者对此2种粒度参数计算方法进行过对比研究。贾建军[17]、刘志杰[18]、毛龙江[19]、徐树建[20-21]等采用图解法公式和矩法公式,分别对山东半岛月湖地区、南海表层沉积物、南京下蜀黄土、末次冰期旋回风成沉积物和陇西盆地晚更新世风成堆积物样品的粒度参数进行了定量计算,并对2种方法所得结果进行了对比研究。认为,图解法反映样品的1个子样的粒度特征,而矩法则反映了样品的总体特征。在进行沉积环境分析时,应充分考虑2种方法的差异。

尽管关于粒度参数及其计算方法已有诸多探讨,但目前没有文献讨论关于粒级划分在粒度参数处理中的作用问题。常用的粒级间距主要有Φ、Φ/2、Φ/4,《海洋地质调查技术规程》中要求采用Φ/4。作者之所以关注这一问题,是因为在实际工作中经常有资料方要求提供多种粒级划分条件下的粒度参数结果。直观上,以Φ/4为粒级间距的参数计算结果较另两者更为准确,然而长期的数据处理经验和统计学方法的验证告诉作者,在实际工作中是可以只采用1种粒级间距来处理粒度参数的,而这样处理并不会影响结果的准确度,同时可以减少数据处理的工作量。

1 材料及前处理方法

1.1 材料来源及组成

本文中的样品来自908专项。考虑到粒度分布可能给参数计算结果带来影响,作者选取了3种沉积物类型共136个底质样品。其中偏粗颗粒的粉砂质砂(TS)50个、偏细颗粒的黏土质粉砂(YT)50个以及粒度分布相对宽泛均等的砂-粉砂-黏土(STY)36个。个别样品中含有一定量有机质,全部样品未见明显碳酸钙成分。

1.2 前处理方法

为保证结果的可对比性及减小误差,全部样品采用Mastersizer2000激光粒度仪进行粒度分析测试。该仪器可测量0.02～2 000μm直径范围的沉积物颗粒。由于本项研究主要是针对沉积物粒级划分对计算参数的影响,故需去除有机质和碳酸钙成分,只保留沉积物颗粒。因此对样品进行了如下前处理,根据海洋底质调查技术进规程[1]的要求,加入体积分数>30%的过氧化氢数滴至样品刚好被全部淹没,待不再冒泡后加入0.25 mol/L的盐酸至不再冒气泡。而后加入蒸馏水,用玻璃棒搅拌后静置24 h,然后将杯中上层清液吸去,再加入蒸馏水,用玻璃棒搅拌,再静置24 h,并用Ph试纸测试烧杯内液体的酸度,直至中性。最后加入数滴0.5 mol/L的六偏磷酸钠,用玻璃棒搅拌或超声波振荡使样品充分分散后上机测试。实验结束后,运用内插值法分别以Φ、Φ/2、Φ/4为粒级间距输出3组粒级频率及D5、D16、D25、D50、D75、D84、D95等数据。而后,将这些数据根据图解法和矩法公式需要进行整理后代入公式进行计算,分别求得每一类沉积物的图解法粒度参数和矩法粒度参数的分间距结果。最后,引入统计学中的单因素方差分析法,判定粒度参数对粒级划分的响应关系。

2 常用粒度参数及计算、统计方法

2.1 常用粒度参数

目前广泛使用的粒度参数包括平均粒径、分选系数、偏态和峰态等。平均粒径(M z)代表着粒度分布的集中趋势,它在一定程度上取决于物源区的粒度分布。分选系数(标准偏差)(δ1)表示粒径频率曲线的扩散程度,反映沉积分选的好坏。偏态(SK1)可量度颗粒频率分布的对称程度,并表明平均值(平均粒径)与中位数(中值粒径)的相对位置。峰态(KG)用来量度粒度分布曲线的尖锐或钝圆的程度。

2.2 粒度参数的计算方法

作者分别采用Folk-Ward(1957)图解法公式和M c Manus(1988)矩法公式对粒度参数进行了计算。Folk-Ward(1957)图解法公式物理意义明确,精确度很高,应用最为广泛,也是国家海洋局海洋地质调查规范(国家海洋局,1975)规定的计算公式;M c M anus(1988)矩法公式采用分组计算的方法,并对高阶矩进行了削阶处理,减少了计算量。

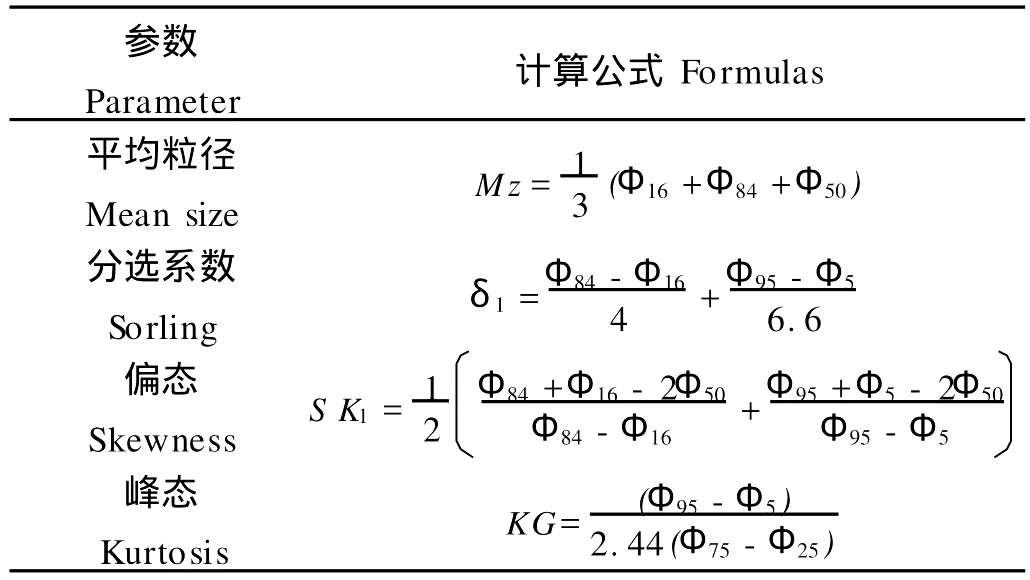
表1 Folk-Ward图解法公式Table 1 Formulasof Folk-Ward graphic methods

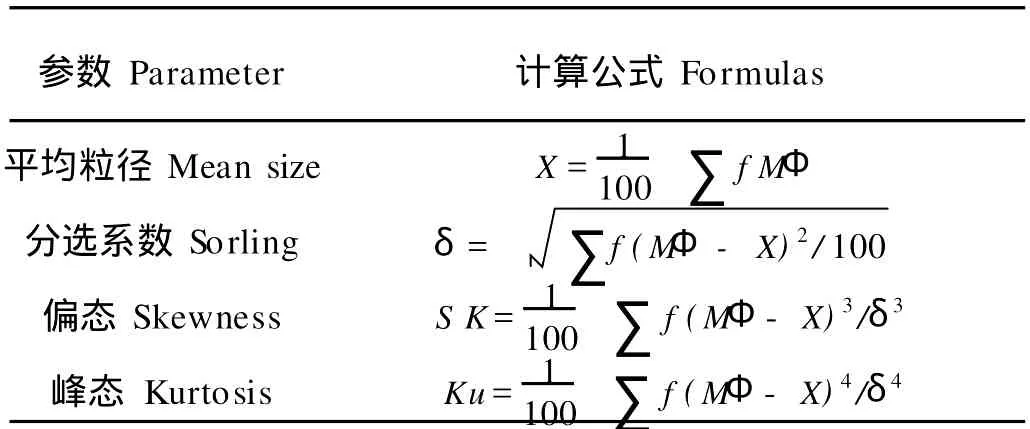
表2 M c Manus矩法公式Table 2 Formulasof M c Manusmomentmethods

2.3 单因素方差分析法——量化粒度参数对粒级划分的响应关系的统计学[2-3]方法

方差分析研究的是分类型自变量对数值型因变量的影响,所采用的方法是检验各总体的均值是否相等。本文意在检验各粒度参数计算方法中,粒级划分对粒度参数值的影响,是一个分类型自变量对一个数值型因变量的影响问题,属于单因素方差分析。分析步骤包括:(1)搭建数据结构模型;(2)建立假设;(3)构造检验统计量;(4)列出方差分析表;(5)统计决策。

3 结果与判定

3.1 粒度参数的计算结果

从表3中对比可以定性地看出,无论是在图解法结果中还是在矩法结果中,各类沉积物各粒度参数的分间距结果基本一致,粒级划分对粒度参数结果没有实质性影响。然而,要确认这一现象为事实结论还需要进行量化分析证明,于是引入统计学中的单因素方差分析法进行判定。

3.2 粒度参数对粒级划分的响应状况判定

3.2.1 搭建数据结构模型 设因素“粒级划分”有3个不同水平“Φ间距、Φ/2间距、Φ/4间距”,在每一个水平下分别应用矩法和图解法分3类沉积物对类“粒度参数”进行136次独立试验,得到表3的结果。

表3 不同水平下的样本观测值Table 3 Experimental data under different treatments

3.2.2 建立假设 欲检验图解法或矩法计算结果中,类“粒度参数”在因素“粒级划分”的3个水平“Φ间距、Φ/2间距、Φ/4间距”下的均值是否相等,需要提出如下形式的假设,即对每一个参数都有:

(1)H0:μ1=μ2=μ3,粒级划分对粒度参数值没有影响,

(2)H1:μ1,μ2,μ3不全相等,粒级划分对粒度参数值有影响

式中,μi为第i个水平的均值。

3.2.3 构造并计算检验统计量 为检验H0是否成立,需要将有关数据代入以下公式,计算相应检验统计量。

(1)各样本均值:

(2)全部观测值的总均值:

(3)误差平方和:

①总误差平方和SST:

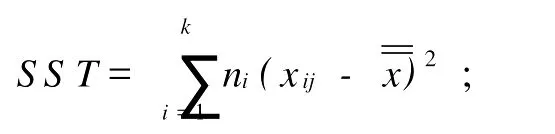
②水平项误差平方和SSA:

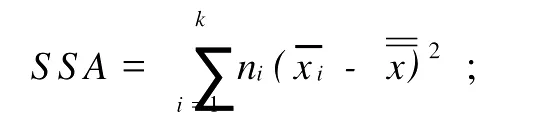
③误差项平方和SSE:

(4)方差

①组间方差M SA:

②组内方差M SE:

(5)检验统计量F:

3.2.4 列出方差分析表 全部计算可通过Excel工作表按照步骤【工具】——【数据分析】——【方差分析:单因素方差分析】完成,计算结果汇入表4和5。

表4 方差分析表Ⅰ(矩法)Table 4 Analysis of variance tableⅠ(Moments M ethod)

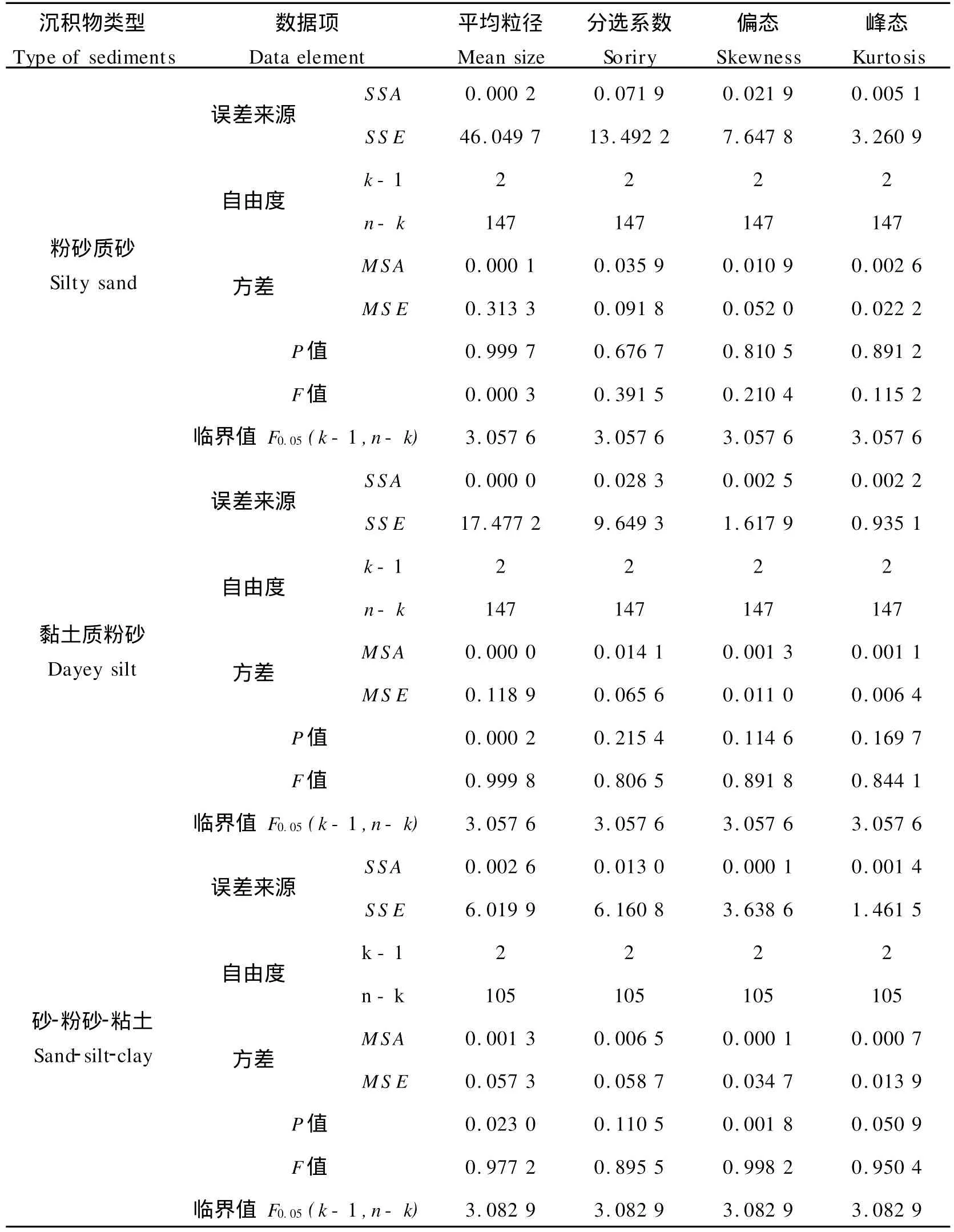
表5 方差分析表Ⅱ(图解法)Table 5 Analysisof variance tableⅡ(Graphic method)

3.2.5 统计决策 根据统计学的描述,对于给定的显著性水平α和求得的自由度k-1、n-k,可以在F分布表中查找到相应的临界值Fα(k-1,n-k)。若F>Fα,则拒绝原假设H0,即所检验的因素对观测值有影响;若F≤Fα,则接受原假设H0,即所检验的因素对观测值没有影响。

由上述列表中的F值与显著性水平为0.05的临界值F0.05的对比结果可知,全部的F值均小于相应的F0.05,统计结果接受原假设H0,即粒级划分对粒度参数的计算结果没有影响,不因沉积物类型和粒度参数计算方法的不同而有不同。

4 沉积物在不同粒级间距下的粒度频率曲线

如前所述,3种粒级间距通过内插值方法取得,则粒级间距的大小必然影响粒度频率曲线上特征点的个数及每一点所对应的频率,进而影响曲线的形态。

如图1所示,一方面,各类型沉积物的粒度频率曲线的形态随粒级间距的不同会有变化:比较Φ/4间距和Φ间距时的曲线能够看出,前者曲线不甚平滑,曲线上的微小波动比较明显,而后者的曲线呈平滑状,基本没有细小变化出现。例如,砂-粉砂-黏土图中显示,3种间距下,在粒径为0.1和0.01 mm附近均有一较大峰值。但在Φ/4间距时,曲线在0.1～0.01 mm之间有细小的较为复杂的波动,而在Φ间距时,曲线较为平滑。由此可知,粒级划分越细,频率曲线上的细微变化被体现得越充分,越有助于更好地辨识沉积过程中的沉积环境、动力状况和物质来源,察觉环境中的细微变化。

另一方面,同一粒径所对应的频率值在不同粒级间距下有较大差别,Φ间距时的频率值约为Φ/2间距时的2倍、Φ/4间距时的4倍。曲线位置高低对比明显,峰值频率处尤为突出。这是因为:同一样品在某一粒径范围内,粒级划分越粗,代表点越少,每一点分担的相对百分含量(频率值)越大,频率曲线的总体位置会越高;相反,粒级划分越细,代表点越多,每一点分担的相对百分含量(频率值)越小,频率曲线的总体位置会越低。这一差别在优势粒级或敏感粒组所对应的峰值频率处尤为突出。由此可以看出,不同粒级间距下,同一沉积物的优势粒级或敏感粒组的代表粒径基本相同,但其相对百分含量差异较大。在利用频率曲线进行环境状况分析时,这种差异会对结果产生较大影响。所以,在进行动力条件和沉积环境等研究时,必须对粒级间距在粒度分析中的影响给予足够重视。

图1 不同粒级间距下沉积物粒度频率曲线Fig.1 Grain-size frequency curves of sediments under different grade interval

5 结论

(1)采用单因素方差分析法统计各类沉积物在各种计算方法中粒级划分对粒度参数的影响情况,得出粒级划分对粒度参数表征粒度分布特征不构成影响。因此在进行粒度数据处理时,采用Φ间距即可,同时能够减小工作量。

(2)粒度频率曲线形态随粒级间距的不同会有变化。粒级划分越细,这种变化被体现得越充分,即细致的粒级划分有助于更好地辨识沉积过程中的沉积环境、动力状况和物质来源,察觉环境中的细微变化。

(3)同一粒径所对应的频率值在不同粒级间距下有较大差异,Φ间距时的频率值约为Φ/2间距时的2倍、Φ/4间距时的4倍。曲线位置高低对比明显,峰值频率处尤为突出。不同粒级间距下,同一沉积物的优势粒级或敏感粒组的代表粒径基本相同,但其相对百分含量差异较大。在利用频率曲线进行环境状况分析时,这种差异会对结果产生较大影响。所以,在进行动力条件和沉积环境等研究时,必须对粒级间距在粒度分析中的影响给予足够重视。

(4)在进行粒度分析时,如果只求粒度参数,采用Φ间距即可,这样可以减小工作量;如果研究沉积环境,建议采用Φ/4间距。

[1] 国家海洋局908专项办公室.海洋底质调查技术规程[M].北京:海洋出版社,2006:4-7.

[2] 贾俊平.统计学(第二版)[M].北京:清华大学出版社,2006:316-324.

[3] 宗义湘,张润清.统计学[M].北京.中国计量出版社,2006:106-108.

[4] 蒲晓强,陶小晚.南黄海部分典型海域沉积物粒度特征[J].海洋科学,2009,33(8):63-66.

[5] 张富元,章伟艳,杨群慧.南海东部海域沉积物粒度分布特征[J].沉积学报,2003,21(3):452-460.

[6] 陈敬安,万国江,张峰,等.不同时间尺度下的湖泊沉积物记录——以沉积物粒度为例[J].中国科学(D辑),2003,33(6):563-568.

[7] 孙千里,周杰,肖举乐.岱海沉积物粒度特征及其古环境意义[J].海洋地质与第四纪地质,2001,21(1):93-95.

[8] 蒋忠信.砂的中值粒径与分选系数的经验关系及其对沉积环境的反映[J].沉积学报,1985,3(1):128-137.

[9] Juan JoséKasper-Zubillaga.Grain size discrimination between sands of desert and coastal dunes from northwestern Mexico[J].Revista Mexicana de Ciencias Geológicas,2005,22(3):383-390.

[10] G De Falco.Grain size and compositional trends of sediments from Posidonia oceanica meadows to beach shore,Sardinia,western Mediterranean[J].Estuarine,Coastal and Shelf Science,2003,58(2):299-309.

[11] 高抒,Collins M.沉积物粒径趋势与海洋沉积动力学[J].中国科学基金,1998,4:241-246.

[12] 左书华.南汇嘴潮滩沉积物的粒度特征[J].水道港口,2008,29(2):88-93.

[13] 刘永学,张忍顺,陈君.粒径趋势分析法在细颗粒潮坪上的应用[J].南京师范大学学报:自然科学版,2001,24(1):105-109.

[14] 程鹏,高抒.北黄海西部海底沉积物的粒度特征和净输运趋势[J].海洋与湖沼,2000,31(6):604-615.

[15] 李安春,陈丽蓉,Eisma D.伊姆斯-道拉德河口悬浮体絮凝过程及其控制因素[J].海洋与湖沼,1996,27(2):138-144.

[16] 夏福兴,Eisma D.长江口悬浮颗粒有机絮凝研究[J].华东师范大学学报:自然科学版,1991(1):66-70.

[17] 贾建军,高抒,薛允传.图解法与矩法沉积物粒度参数的比较[J].海洋与湖沼,2002,33(6):577-582.

[18] 刘志杰,龙海燕.南海沉积物图解法和矩值法粒度参数计算及其对比[J].中国海洋大学学报,2009,39(2):313-316.

[19] 毛龙江,庞奖励,刘晓燕.南京下蜀黄土图解法与矩值法粒度参数对比研究[J].陕西师范大学学报,2007,35(3):95-99.

[20] 徐树建,潘保田,张慧,等.末次冰期旋回风成沉积物图解法与矩值法粒度参数的对比[J].干旱区地理,2005,28(2):194-197.

[21] 徐树建,潘保田,陈莹莹,等.陇西盆地晚更新世风成堆积物粒度参数的对比[J].海洋地质与第四纪地质,2005,25(3):145-150.

The Responses of Grain-Size Parameters to Grade Interval

FU Li-Li,FENG Xiu-Li,YANG Xu-Hui
(College of Marine Geo-Science,Ocean University of China,Qingdao 266100,China)

In o rder to find the responses of grain-size parameters to grade interval,this article calculated the grain size parameters of 136 sediment samp les of three types:silty sand,clayey silt,and sand-siltclay,respectively by the Folk-Ward Graphic method and the M c M anus moment method,under three grade intervals:Φ,Φ/2,andΦ/4.The ANOVA statistical analysis was introduced to carry out the comparison of the results.It show ed that the grade interval didnπt affect grain size parameters,no matter calculated by which method and which type the sediment is.The narrower the grade interval is,the better the change of the shape of frequency curve is em bodied,and frequencies of the same grain diameter w ere quite different under different grade interval.Therefore,when the dynamic condition and sedimentary environment w ere studied,the effect of grade interval on grain size analysismust be valued sufficiently.Φ can be used to calculate grain size parameters,w hich can reduce the workload,while to detect subtle changes in the environment,Φ/4 is recommended.

grade interval;grain-size parameters;graphicmethod;momentmethod;ANOVA statistical analysis;frequency curve

P736.21

A

1672-5174(2011)09-083-07

2010-11-15;

2011-06-14

付莉莉(1980-),女,硕士生。E-mail:fulily2008@gmail.com

责任编辑 徐 环