一种确定挖方边坡开挖松弛区的数值分析方法

王 浩

（福州大学环境与资源学院，福州350108）

一种确定挖方边坡开挖松弛区的数值分析方法

王 浩

（福州大学环境与资源学院，福州350108）

基于挖方边坡应力重分布与应变局部化过程的数值模拟，将边坡开挖松弛过程划分为弹性松弛、塑性松弛产生、塑性松弛扩大和整体松弛失稳4个阶段；分析结果表明：正负分区揭示边坡开挖松弛的力学本质，可以用来确定开挖松弛区的范围，进而提出接近挖方坡面的开挖松驰区（负值区）、远离开挖坡面的原岩应力区（零值区）和介于两者之间的应力集聚区（正值区）的分区方案；并通过与相关方法的比较，表明该方法力学概念明确，计算方法简单，是挖方边坡设计中确定开挖松弛区的实用方法。

挖方边坡；开挖卸荷；松弛区；数值模拟

挖方边坡是指因工程建设或矿物开采需要而采取人工、机械或爆破等开挖手段改变原有地形所形成的人工边坡。边坡岩土体在开挖坡形改变和开挖过程扰动的共同作用下产生应力重分布，形成开挖坡面附近一定范围内应力水平急剧降低的区域，称之为边坡开挖松弛区。开挖松弛区内岩土体经历较为复杂的应力重分布过程，其内部存在的微裂纹、微孔洞以及颗粒边界产生局部拉、压、剪应力集中，当应力集中值超过此区域的材料强度时，这些微小裂隙和孔洞便会不断地扩展和相互连接，导致岩土体有效承载面积变小，强度降低，逐步形成一条或数条发生剧烈变形的带状区域，称之为剪切带，也即所谓应变局部化过程。这一过程宏观上表现为边坡卸荷回弹、裂面张开及扩展、新裂隙萌生、岩土体松动、滑移面形成，以及边坡局部或整体破坏解体等演生破坏结果。

挖方边坡的卸荷松弛与变形破坏涉及到工程岩体应力重分布与应变局部化的基本力学问题，自20世纪90年代以来，一直是学界研究焦点问题之一。国外关于工程岩体开挖松弛效应的研究成果主要集中在地下开挖围岩扰动与损伤研究方面［1－3］，研究认为开挖扰动区或开挖损伤区（excavation distur bed zone或excavation damaged zone）内岩体物理力学特性发生了明显变化，岩体类型、地应力和开挖方法是影响开挖扰动区范围与性质的主要因素。国内近年来就边坡开挖松弛区或卸荷带问题进行了研究。盛谦、邓建辉和高大水等［4－6］采用现场调查、工程物探、试验监测和数值计算对三峡船闸边坡开挖松弛区进行了系统研究；黄润秋等［7］提出边坡二次应力的“驼峰应力分布规律”，分析了岩质高边坡卸荷带的形成机理；肖世国等［8］研究了边坡开挖应力场和位移场的分布规律，提出了松动区、塑性变形区和弹性变形区的分区方案。周华等［9］采用主拉应变准则为松弛判据，针对小湾工程坝基松弛问题开展开挖松弛效应有限元分析。

众所周知，确定边坡开挖松弛区的范围是挖方边坡稳定分析与加固设计的基础，当前对边坡开挖松弛问题的研究仍以定性和半定量为基础，尚处于分别研究、各自表述的阶段，在边坡开挖松弛区孕育发展的力学机理、松弛区岩体力学性质弱化效应等方面尚需深入研究。本文通过研究开挖过程中边坡岩土体应力重分布与应变局部化现象，提出一种在边坡稳定分析中快速识别开挖松弛区范围的数值分析方法，并对其适用性和有效性进行了分析。

1 数值模型与计算参数

本文以典型花岗岩类土质挖方高边坡为例概化工程地质模型，并进行有限单元网格离散（图1），研究边坡逐级开挖过程中应力重分布及剪切带发育过程。该计算模型为开挖坡率为1∶1.0，坡高64 m的边坡，采用2000个三角形等参单元离散而成，材料模型为Mohr－Coul o mb弹塑性模型。有限元计算模型基于以下假定：

⑴边坡场区受自重应力场控制；

⑵遵循二维平面应变假定；

⑶不考虑节理和地下水影响；

⑷采用强度折减法计算安全系数。

主要岩土物理力学参数按砂土状强风化花岗岩试验参数并结合福建省工程建设地方标准《岩土工程勘察规范（DBJ13－84－2006）》推荐的“福建风化花岗岩和残积土强度指标”综合选取（表1）。

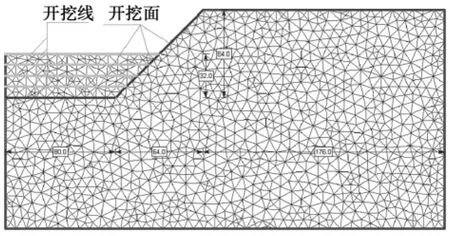
图1 边坡开挖有限单元离散图（已挖4级）Fig.1 Computing mesh of slope excavation by FEM

表1 边坡开挖模型岩体力学参数表Tab.1 Rock mass parameters of slope excavation model

有限元计算在设定边坡自重应力场后，分8级开挖至设计高程。基于挖方边坡应力重分布与应变局部化的力学本质，经分析开挖阶段边坡各应力参量的动态变化特征，选取最大主应力增量Δσ1作为揭示边坡应力重分布过程的特征变量，采用剪应变和屈服区演变规律揭示边坡应变局部化过程。本文讨论的Δσ1定义为边坡开挖前后应力张量之增量的最大主应力分量，Δσ1的获取是通过求取开挖前后坡体单元应力张量之差，然后将应力差值张量在节点上分解到最大主应力分量方向上，而不是简单比较开挖前后最大主应力标量值大小，因此能体现最大主应力方向的偏转，全面表征边坡应力场的变化特征。

2 边坡开挖卸荷松弛过程模拟

通过有限元模拟再现边坡开挖卸荷松弛过程中由Δσ1表征的边坡应力重分布过程，以及边坡剪切带孕育过程（图2），采用强度折减法对各开挖阶段边坡稳定系数进行计算（图3），最终将边坡开挖卸荷松弛分为以下4个阶段。

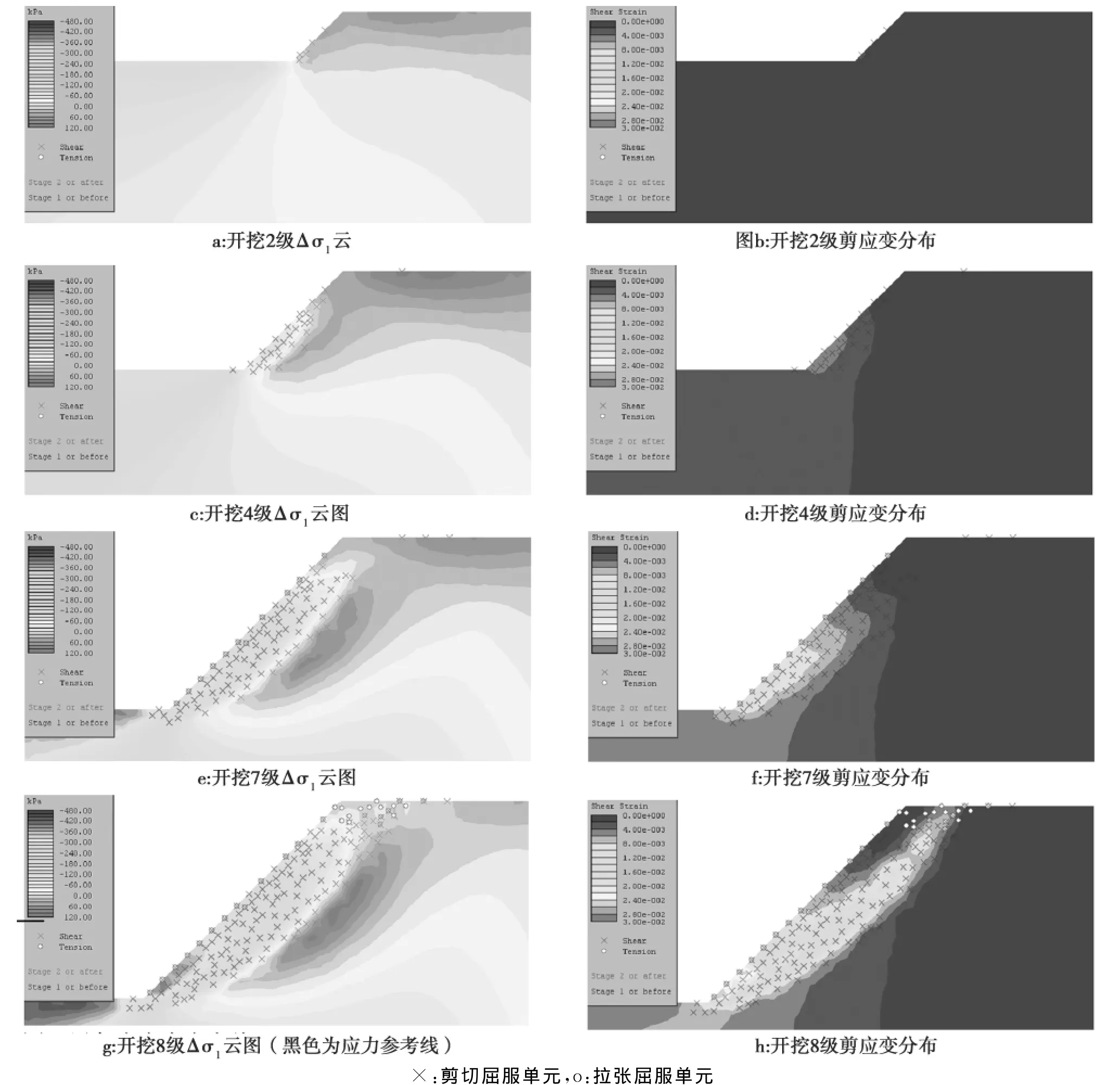
图2 边坡逐级开挖过程的应力重分布与应变局部化Fig.2 Stress redistribution and strain localization during slope excavating

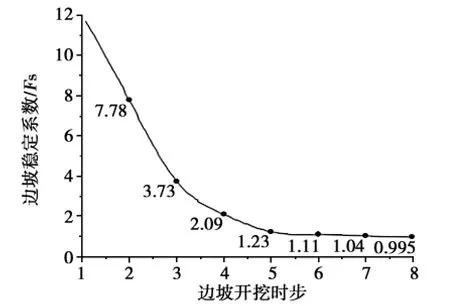
图3 逐级开挖条件下边坡稳定系数Fig.3 Slope stability factor during excavating

图4 水平参考线Δσ1变化图Fig.4 Variety of differential sigma one in the referenced line

（1）弹性松弛阶段。边坡开挖1～2级阶段，边坡应力重分布现象不突出，主要体现为坡脚和坡顶的应力集中，但量值较小，最大约20 k Pa；边坡总体未见明显变形，仅坡脚局部产生剪切屈服。开挖边坡总体处于弹性松弛阶段，边坡稳定系数为7.78。

（2）塑性松弛产生阶段。边坡开挖3～4级阶段，应力重分布现象已较为突出，Δσ1云图可初步按照其量值划分为3个典型区间，即开挖面附近的应力下降区（Δσ1负值区，应力降低最大约120 k Pa），远离开挖面的应力不变区（Δσ1零值区），以及位于两者之间的应力上升区（Δσ1正值区，应力升高最大约50 k Pa）。在应力下降区内，坡体岩土应力水平超出其强度逐步进入塑性剪切屈服状态而承载能力弱化，导致区内岩土体应力水平降低，承载功能逐步向开挖面内侧转移，形成应力水平明显升高的应力上升区，两区紧密相连。开挖边坡处于塑性松弛产生阶段，此时边坡稳定系数为2.09。

（3）塑性松弛扩大阶段。边坡开挖至5～7级阶段，前级开挖的应力上升区（Δσ1正值区）逐步进入屈服状态，并因超载屈服软化而转化应力下降区（Δσ1负值区），应力降低的最大值约为320 k Pa，应力下降区明显向远离坡面方向扩展，并在其内侧扩大形成新的应力上升区（Δσ1正值区），应力升高的最大值约为80 k Pa，应力重分布现象逐渐明显；应力下降区和应力上升区的应力调整水平也明显增大。此阶段开挖边坡塑性剪切变形区逐步扩大，并在开挖坡面新增拉剪屈服区，塑性区呈逐渐连通状态。开挖至第7级时，边坡稳定系数迅速下降为1.04，接近极限平衡状态。

（4）整体松弛失稳阶段。边坡开挖至第8级时，应力下降区（Δσ1负值区）在坡体内侧贯通，应力降低最大值约为390 k Pa，应力水平明显降低；与此同时，应力上升区（Δσ1正值区）应力水平大幅增高，应力升高值约为115 k Pa，二区的范围明显扩展、变化量值急剧增高。此阶段，边坡下部处于剪切屈服状态，坡顶附近则处于拉张屈服状态，最大剪应变呈定向发展趋势，形成破裂面，边坡稳定系数为0.995，开挖边坡处于整体松弛失稳阶段。

基于上述分析，边坡开挖松弛区的形成过程为：边坡开挖逐渐破坏了其原有应力平衡状态并产生应力重分布，导致边坡开挖面附近一定深度范围内的岩土体应力急剧调整，其应力水平上升而超出其强度极限，产生塑性变形；然后，该区域内岩土体力学性质弱化，承载能力下降，应力水平降低；随后，应力重分布逐步向坡体内侧转移，导致开挖松弛区范围逐步扩大；最终，在松弛区范围内，产生塑性破坏的坡体单元逐步扩展而贯通，形成剪切带。

本文讨论的模型主要基于均质岩土体模型，对于非均质岩土体模型，应考虑其结构面分布特征及其对边坡开挖松弛效应的影响对计算结果进行以下修正：当坡体内遍布多组节理时，可将坡体视为均质岩土体，按本文研究方法总体考查其开挖卸荷松弛效应；当坡体内存在影响边坡变形破坏模式的控制性节理时，应在数值模型中引入弱面实体单元，考虑其弱面控制效应，对结构面附近的应力调整与屈服破坏进行专门的考查，使得边坡开挖松弛区的确定范围与工程实际相符。

3 挖方边坡开挖松弛区确定方法

图2g在边坡中部布设了一条水平参考线，沿该水平参考线Δσ1的量值变化和相对分区结果见图4。

结合图2和图4可知边坡开挖松弛区分区的特征为：在开挖坡面附近，存在岩体应力水平显著降低的区域（Δσ1负值区）。该区距离坡面距离为0～20 m之间，区内Δσ1降低的最大值约为390 k Pa，体现塑性区坡体应力水平的强烈松弛效应，区内主应力方向明显偏转，坡体处于塑性变形而承载功能弱化，形成破裂面。在应力降低区内侧存在一个应力急剧升高的区域（Δσ1正值区），而且应力升高区与应力降低区的过渡剧烈。该区距离坡面距离为20～40 m之间，区内Δσ1最大增量值约为115 k Pa，区内应力场量值梯度较大，体现坡体岩土自承载产生的应力集聚现象。在应力升高区内侧的大片区域，坡体应力状态调整量值较小，应力矢量基本保持不变，应力水平与原岩应力相当，体现为原岩应力场。

基于上述分析，在边坡开挖应力重分布过程中，Δσ1是具代表性的特征参量，其力学意义可解释如下：Δσ1负值区经历超载－塑性－软化过程，区内岩土体进入塑性软化状态，定义为开挖松弛区；由于应力重分布，Δσ1正值区成为主要的承载区，区内岩土体处于弹性加载状态，定义为应力集聚区；Δσ1零值区应力重分布现象很小，定义为原岩应力区。最终建立边坡开挖松弛区的划分原则见表2。

表2 边坡开挖松弛区的划分原则Tab.2 Partition principle of relaxation zone during excavating

数值模拟计算结果的后处理需要从复杂的计算成果中排除干扰信息，提取出反应边坡开挖松弛力学本质的核心信息。根据计算分析的经验，主要以Δσ1＝0等值线为划分界线，兼而考虑拉张屈服部位和应变过渡状态，对开挖松弛区、应力集聚区和原岩应力区进行三场划分（图5），力学概念清晰，分区界线明确。

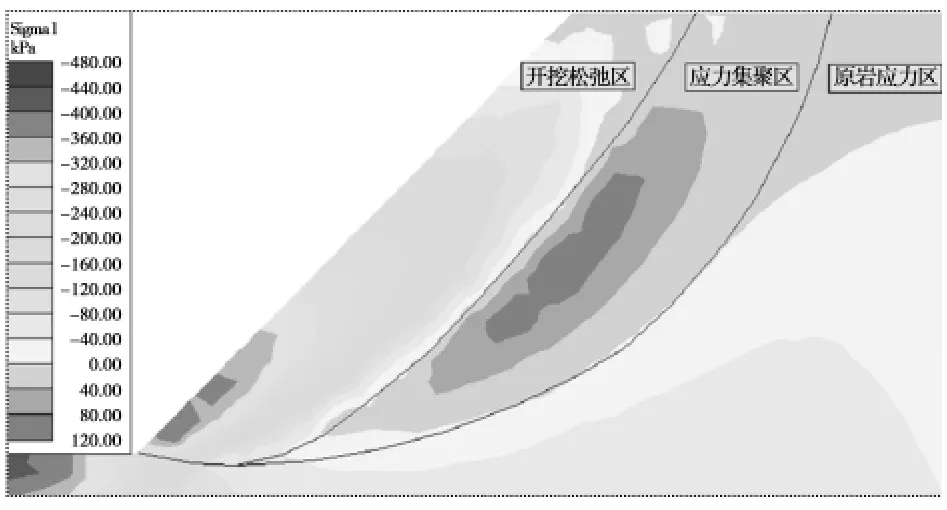
图5 边坡开挖卸荷松弛各影响区分布图Fig.5 Distribution chart of excavation disturbed zone

4 讨论

挖方边坡开挖松弛区的确定方法除了耗资惊人的工程物探和监测手段外，主要有3种数值方法：第1种是根据边坡变形场的水平位移突变位置确定开挖松弛区的内边界，第2种是根据边坡岩土体稳定系数突变点位置确定开挖松弛区内边界［9］；第3种是本文根据边坡应力场Δσ1量值提出的Δσ1增减变化划分松弛区边界。

图6是开挖7级时这3种划分方案实施效果的对比分析图。

由图6可见：即使边坡已经接近极限平衡状态（Fs＝1.04），但由于坡体变形场存在较多的干扰信息，仍无法准确识别开挖松弛区的位移突变部位，因此很难区分开挖松弛区的范围。另外，通过边坡稳定系数增量云图可大体确定开挖松弛区范围，但由于拉张和剪切破坏部位稳定系数差异明显，对稳定系数突变位置的识别也不够准确。第1、2种方法其关键的“突变点”位置不明确或规律性不强，因此，工程应用将有相当的局限性。

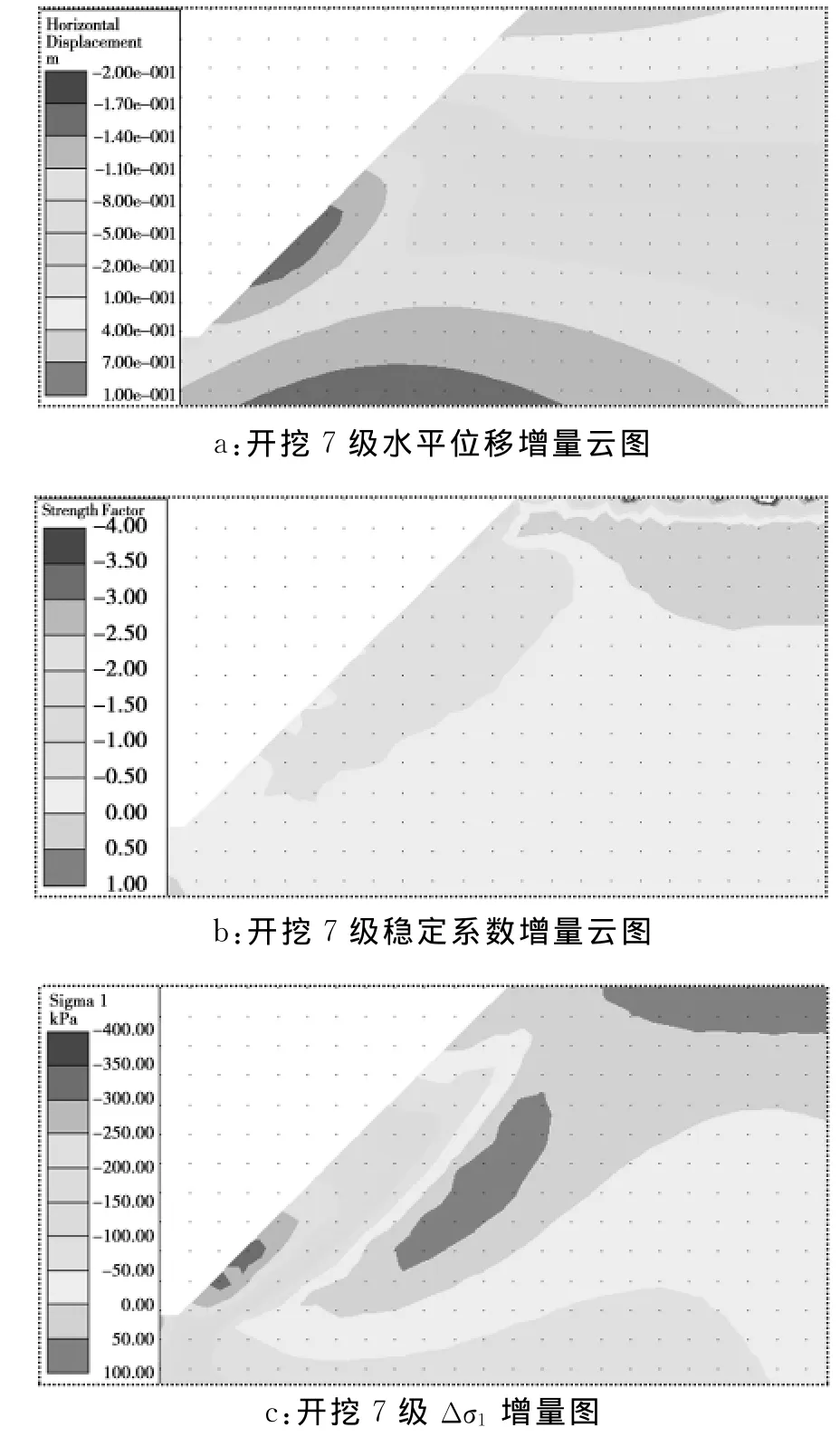
图6 边坡开挖松弛数值分析方法对比图Fig.6 Comparison chart of three method to deter mine excavation disturbed zone

本文提出的第3种方法，由于Δσ1在开挖松弛区为负值，在应力集聚区为正值，正负分界明确，物理概念清晰，计算方法简单，便于工程应用（图6）。同时，在边坡数值分析过程中，由于岩土体变形模量参数离散性较大，变形场的计算结果可信度较低，常存在数量级的差别，而边坡应力场则相对较为稳定，其计算结果较为可靠。

5 结语

（1）本文采用有限单元法研究了典型挖方边坡的应力重分布与应变局部化过程，并将其划分为弹性松弛形、塑性松弛产生、塑性松弛扩大和整体松弛失稳4个阶段。

（2）挖方边坡应力场的Δσ1正负分区反应了边坡开挖卸荷松弛的力学本质，Δσ1负值区可表征开挖松弛区范围，Δσ1正值区可表征应力集聚区范围，Δσ1零值区可表征原岩应力区范围。

（3）采用Δσ1正负分区和塑性区孕育过程为标准，提出接近开挖坡面的开挖松驰区、远离开挖坡面的原岩应力区和介于两者之间的应力集聚区的三场分区方案；并通过与其他数值方法的比较，表明该方法物理概念清晰，计算方法简单，是挖方边坡设计过程中的实用方法。

［1］Autio J，Siitari－Kauppi M，Timonen J，et al.Deter mination of the porosity，per meability and diffusivity of rock in the excavation－disturbed zone around full－scale deposition holes using the 14C－PMMA and He－gas methods［J］.Journal of Contaminant Hydrology，1998，35：19－29.

［2］Sato T，Kikuchi T，Sugihara K.In－situ experiments on an excavation disturbed zone induced by mechanical excavati on in Neogene sedimentary rock at Tono mine，central Japan［J］.Engineering Geology，2000，56：97－108.

［3］Schuster K，Alheid H J，Boddener D.Seismic investigation of t he excavation damaged zone in opalinus clay［J］.Engineering Geology，2001，61：189－197.

［4］盛谦.深挖岩质边坡开挖扰动区与工程岩体力学性状研究［D］.武汉：中国科学院武汉岩土力学研究所，2002.

［5］邓建辉，李焯芬，葛修润.岩石边坡松动区与位移反分析［J］.岩石力学与工程学报，2001，20（2）：171－174.

［6］高大水，徐麟祥.三峡工程船闸中隔墩岩体利用及力学性状研究［J］.岩石力学与工程学报，2006，25（9）：1932－1936.

［7］黄润秋，林峰，陈德基，等.岩质高边坡卸荷带形成及其工程性状研究［J］.工程地质学报，2001，9（3）：227－232.

［8］肖世国，周德培.开挖边坡松弛区的确定与数值分析方法［J］.西南交通大学学报，2003，38（3）：318－322.

［9］周华，汪卫明，陈胜宏.岩体开挖松弛的判据与有限元分析［J］.华中科技大学学报：自然科学版，2009，37（6）：112－116.

A Numerical Analysis Method to Confir m the Range of Relaxation Zone during Slope Excavating

WANG Hao
（College of Environment and Resources，Fuzhou University，Fuzhou，350108，China）

Accor ding to numerical simulation of stress redistribution and strain localization during slope excavating，the excavation relaxation process is divided into four stages：such as elastic relaxation stage，plastic relaxation generating stage：plastic relaxation expanding stage and integral relaxation instability stage.Distribution of positive or negative zone for differential sigma one which is obtained by subtracting the stress tensors before and after excavated disclose mechanics characteristic of excavation relaxation zone，and can be used to confirm the range of relaxation zone.And then，excavation relaxation zone near excavation surface，original stress zone far from excavation surface and stress concentration zone bet ween above two are partitioned.Finally，compared with relative methods，this partitioned scheme is proved to be use full during stability analysis for cutting slopes because of its clear mechanics conception and simple calculation process.

cutting slope；excavation unloading；relaxation zone；numerical simulation

S511.01；Q789

A

1007－7383（2011）05－0623－06

2011－06－06

国家自然科学青年基金项目（41002127），福建省青年人才创新基金项目（2008F3060）

王浩（1978－），男，讲师，从事岩土工程研究；e－mail：h＿wang＠126.co m。