函数极值在经济管理中的应用

2011-01-04王洪涛

山东开放大学学报 2011年2期

关键词：充分条件驻点订货

王洪涛

（荣成广播电视大学，山东荣成 264300）

函数极值在经济管理中的应用

王洪涛

（荣成广播电视大学，山东荣成 264300）

在经济迅速发展的今天，竞争日趋激烈，怎样才能达到投入小，产出多，成本低，效益高，利润大的效果，本文通过对市场需求、利润、成本和库存四个问题分析来浅谈函数极值理论在经济管理中应用。研究某些商品市场需求量，企业获得最大利润的生产量，获得最大利润的最小成本等问题用的是一元函数极值理论，同时也验证了经济学中的有关命题。在解决库存管理中以最低的库存和费用使相关业务取得最大效益问题，通过建立数学建模，利用多元函数极值理论求出最优订货周期。文中给出了函数极值理论的相关定理及求解函数极值的具体步骤。

函数极值；多元函数；库存管理

一、引言

经济快速发展，企业要想生存和发展，经济管理是否科学是非常重要的。现在几乎每一个经济学领域都用到数学，对于企业的决策者和管理者来说都至关重要。企业如何决定生产量，使生产成本最小。生产量少于市场需求量，则无法满足市场的需求，企业无法获得最大利润；生产量大于市场需求量，造成一部分成本的损失。现今各个企业都会面临库存管理尤其是超市之类的零售企业，在保证经济正常运行的前提下，科学合理的分析市场需求，花费最小成本，获得最大利润，以最低限度的库存和费用使有关业务取得最大效益，就成为人们关注的问题，本文通过利用导数的方法求解极值，并给出求一元及多元函数极值的方法。研究产量和价格与最大利润的关系。利用多元函数极值理论求解最优库存量，其优点是能够提高企业管理的效率，也是企业的科学化、正规化管理，与世界接轨的重要条件。在我国现阶段正在进行经济增长转型的时期，它的作用会更大。

在求解获得最大利润时的产量和产品销售的价格，有的文章只是简单提及用函数极值理论求的最优价格和产量，本文注重对数学结果做定性的分析，明确提出它在生活中的实际意义，即利用极值的概念对需求函数进行分析之后，我们可以了解这种商品在市场的需求变化和饱和程度。

在研究某些商品市场需求量时，企业获得最大利润的生产量，获得最大利润的最小成本等问题引入了恩格尔函数，同时也验证了经济学中的有关命题。在解决库存管理问题时，要求的最优的订货批量，利用数学建模的思想把实际问题转化为数学问题，利用极值解决此问题的方法，与其他注重介绍建模思想的相区别开来。

接下来我们首先给出一元函数极值理论和多元函数极值理论的有关定理，及求解极值的步骤。

二、一元函数极值理论

1.有关定理

下面给出几个极值的充分条件。

定理1（第一充分条件）。设函数f（x）在x0的一个邻域内可导，若当x在该邻域内由小于x0连续地变大为x0，其导数f′（x）改变符号，则f（x0）为函数的极值，x0为函数的极值点。若导数f′（x）由正值变为负值，则x0为极大值点，f（x0）为f（x）的极大值，若导数f′（x）由负值变为正值，则x0为极小值点，f（x0）为f（x）的极小值。

由此可知，如果f（x）在x0处可导且f′（x）=0，但f′（x）在x0的两侧同号，则x0不是f（x）的极值点，f（x）在x0处不取得极值。

定理2（第二充分条件）。设函数f（x）在x0处的二阶导数存在，若f′（x0）=0，且f″（x0）≠0，则x0是函数的极值点，f（x0）为f（x）的极值，并且当f″（x0）＞0时，x0为极小值点，f（x0）为极小值；当f″（x0）<0时，x0为极大值点，f（x0）为极大值。

应当注意的是如果f′（x）=0且f″（x）=0，或者f′（x）=0，但f″（x）不存在，那么一元函数极值的第二充分条件就失效了，此时可以考虑运用一元函数极值的第一充分条件。

2.求一元函数极值的步骤

我们经常用上面的充分条件来求一元函数的极值，下面给出求一元函数极值的步骤。

（1）确定函数的定义域；

（2）令f′（x）=0，求出所有的驻点，考察f′（x）每个驻点左右的符号，相反的取极值，否则不取极值；

（3）若f′（x0）=0，f″（x0）≠0。当f″（x0）＜0时，f（x）在x0取极大值，当f″（x0）＞0时，f（x）在x0取极小值；

（4）求出各极值点处的函数值，就得到相应的极值。

特别要注意的是当一阶导数不存在的时候的求法，例如｜x-1｜在x=1点的极值，

三、多元函数极值的有关理论

1.有关定理

类似于一元函数求极值的判定，多元函数极值有如下定理。

定理3（必要条件）设E为n元行向量空间，

（x1，x2，…，xn）∈E。 n元函数f（x1，x2，…，xn）：E→1R，若f在点P0，（）可微且取极值，则

（1）P0必为f的驻点f′（P0）=0；

（2）若f在U（P0）存在连续的二阶偏导数，A为f在P0的Hesse矩阵，则

1）f在点P0取极小值时，Hesse矩阵A为正定或半正定；

2）f在点P0取极大值时，Hesse矩阵A为负定或半负定；

3）f在点P0不取极值时，Hesse矩阵A为非定号。

注f（x1，x2，…xn）在点P0（）处存在一阶偏导数，则极值点必为驻点，但驻点不一定是极值点，当f（x1，x2，…，xn）在点P0（）处不存在一阶偏导数时，P0（）也可能是f（x1，x2，…，xn）的极值点。即极值点可能是驻点或一阶偏导数不存在的点。

定理4（充分条件）设E为n元行向量，

（x1，x2，…，xn）∈E。如果函数y=f（x1，x2，…，xn）在驻点P0（）的某邻域U（p0）内，具有Hesse矩阵A，则

（1）若A为正定（或负定）矩阵时，f在点P0取极小（或极大）值；

（2）若A为半正定（或半负定）矩阵时，f在点P0取极小（或极大）值；

（3）若A为非定号矩阵时，f在点P0不取极值。

注求函数y=f（x1，x2…，xn）的极值时，应首先求出驻点或偏导数不存在的点，然后对所有可能的极值点进行检验，确定函数的极值点并求出函数极值。

2.多元函数求解极值的方法

第一步：求出函数f（x1，x2…，xn）可能的极值点。首先，求出函数f（x1，x2…，xn）的驻点，根据极值存在的必要条件，解方程组

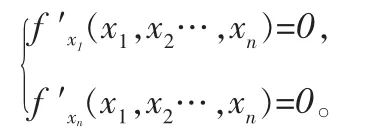
方程组的解即为驻点。然后考虑一阶偏导数不存在的点。

第二步：对每一个可能的极值点p0（）进行检验，根据极值存在的充分条件，首先，计算f（x1，x2，…，xn）在点P0（）的Hesse矩阵A，

再根据定理4判断P0（）是否为极值点并求出极值。

四、应用

1.市场需求分析

影响需求的因素包括影响购买愿望与购买能力的各种经济与社会因素，这些因素主要是：价格、收入、消费者嗜好与预期。如果把消费者的收入作为主要因素，而把其他因素都视为固定的，则商品需求量依消费者收入变化的函数关系，称为恩格尔函数。在经济学中，如果某种商品的恩格尔函数是单调递增的，则称该商品为正常商品，如果是单调递减的，则为劣质商品。

通过市场对恩格尔函数图形及极值的分析，我们可以了解该种商品市场需求量的变化。当收入为零时，需求量Q表示人们无收入时的需求量；当收入无限多时，需求量Q表示该商品市场饱和时的需求量。

解首先求需求函数Q（x）的一阶导数

因此，对这种商品的需求量随收入的减少而减少，这种商品是正常商品，又

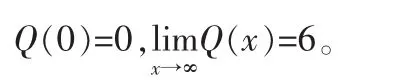
人们的收入为零时，市场对该种商品的需求量为零.市场对该种商品的饱和需求量为6。

利用极值的概念对需求函数进行分析之后，我们可以了解这种商品在市场的需求变化和饱和程度。

例2 设一地区对高级唱片的需求量Q随着人们收入的恩格尔函数Q（x）=。讨论随着该地区收入的增加，对这种高级唱片需求的变化趋势。

解首先求需求函数Q（x）的一阶导数和二阶导数

市场对该种商品的需求量Q随收入的增加而增加，这种商品是正常的。又

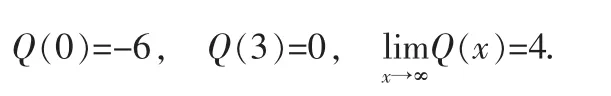
这说明当人们的收入为零时，基本生活需求无法得到满足，人们不会考虑这种唱片。只有当收入大于3，人们才会对这种高级唱片有需求，但也不是无限的，人们的收入无穷时，市场对此商品的饱和需求量为4。

下面来讨论耐用消费品的需求函数。

耐用消费品是指那些使用寿命较长，一般可多次使用的消费品.耐用消费品由于购买次数少，因而消费者的购买行为和决策较慎重。耐用消费品的典型适用产品如：家用电器、家具、汽车等。

我们利用导数分析耐用消费品的需求量是如何随价格变化的。

例3 设一地区对私人飞机的需求量为Q，经过多年的统计分析得出需求函数为Q（P）=-2P3+12P2-3P+8。

得到驻点

当P=0时Q=8，即白送时最大需求量为8；

当0＜P＜2时，Q″（P）＞0，曲线上凸；

当时，Q′（P）＞0，需求随价格P增加仍呈上升趋势；

2.最大利润问题

在经济学中，总收入和总成本都可以表示为常量x的函数分别为R（x）和C（x），其中x表示生产或销售过程中影响收入和成本的某一因素，则总利润L（x）可以表示为

为使总利润最大，其一阶导数需要等于零，即

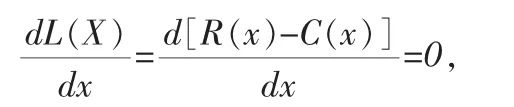
由此可得

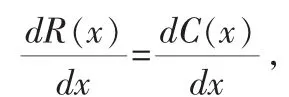
根据极值存在的二阶充分条件，为使总利润最大，还要求二阶导数

由此可得

这就是说，在获得最大利润的常量处，必须要求边际收益等于边际成本。但此时若又有边际收益对常量的微商小于边际成本对常量的微商，则该常量一定能使企业获得最大利润。

例4 设某厂生产一商品的总成本函数为C（x）=20+2Q，需求函数，其中为p价格，Q为产量，求总利润最大时的产量及最大利润。

解由于总收入

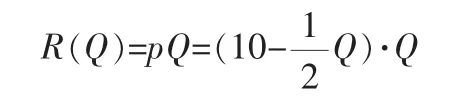
因此由式（4-1）得

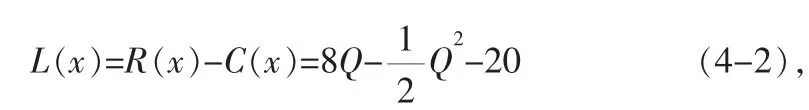
对（4-2）求一阶导数得

因此其唯一的驻点Q0=8，

对（4-2）求二阶导数

故L在Q=8时取得最大值

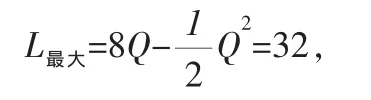
即当产量为8时总利润最大，最大利润为32。

3. 成本最低问题

成本最低化又称成本极小化、最低成本点.所谓成本最低化，就是根据成本目标管理的任务，通过分析降低成本的各种因素，制定可能实现的最低成本目标，并以此为依据进行有效的控制和管理，使实际管理结果达到最低成本目标.在生产实际中，经常遇到这样的问题：在既定的生产条件下，如何生产能使成本最低，利润最大。

设某企业某种产品的生产量为x，C代表总成本，于是x处的边际成本为C′=c′（x），而生产每单位产品的平均成本为

因而，c′（x）=g（x）+xg（x）。

由极值存在的必要条件知道，使平均成本最小的生产量x，应满足g（x0）=0代入上式得

这是经济学中的又一重要结论，使平均成本最小的生产量x0正是边际成本等于平均成本的生产量x0。

例5 设某厂加工一件羊皮的成本为C（x），其中表示加工的数量羊皮，成本函数为c（x）=60+24x+2x2，试求平均成本的产量水平。

解由（4-3）知平均成本

4. 库存问题

经济活动离不开存储，存量过多会造成资金积压和资源的闲置；存量不足又将面临供不应求而影响生产活动的正常进行或丧失获利良机。因此，在保证经济活动正常进行的前提下，要科学地作出存货决策，以最低限度的库存量和费用，使有关业务活动取得最大效益。

假定Q为订货批量；P为单位产品的销售价格；D产品每天的需求量；A为每次订货的订货费；C为单位产品的进价；H为单位产品单位时间的库存保管费；T为订货周期；L为1个周期内的平均总利润.易得由此每次订货批量（即订货时的订货量）和订货周期的长度分别为：

从而每次支付的产品购买费为CQ，在1个周期内任意时刻t的库存量为Q-DT，在1个订货周期T内的库存保管费为：

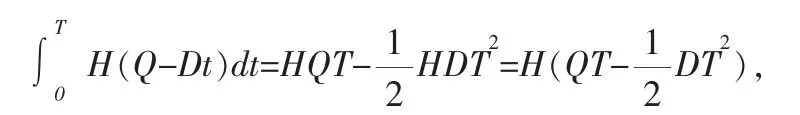
于是库存系统在1个周期内的平均总利润为

L=［毛利-（订货费+购买费+库存费）］/T

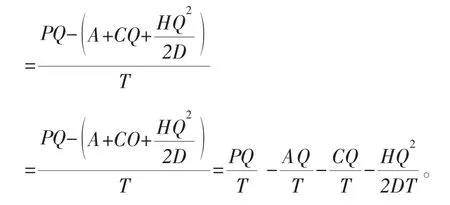
将（4-4）式代入得

现假设需求率是价格的线性函数D=a-bp，其中a＞0，b＞0，a-bp＞0，此时，平均总利润函数（4-5）变为：

下面求出最优解，即最优库存量、销售价格和订货周期.

将式（4-6）视为Q、P的二元函数，并记为L=L（Q-P）（Q＞0，P＞0），

令

结合（4-6）得

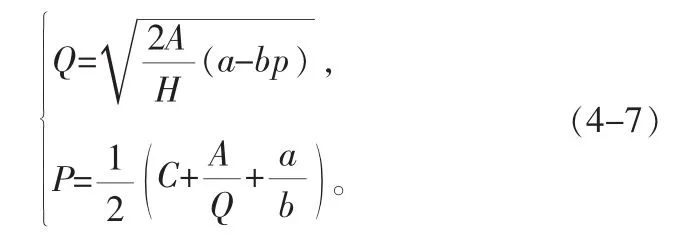
显然，直接求解该方程组是比较复杂的，不妨设该方程组的解为（Q*，P*）

Hesse矩阵的行列式为

所以，根据多元函数的极值理论可知，当detΔ＜0时，

即

函数L（Q，P）具有极大值点，从而（Q*，P*）即为所求。

将式（3-4）中的P代入Q可得

五、结论

总之，函数极值在经济管理中的应用非常广泛，其作用是使厂商花费最小的成本，获取最大的利润，以最低限度的库存量和费用，使有关业务活动取得最大效益。当然经济发展千变万化，使企业在激烈的市场竞争中争得一席之地。我们还可以看到解决错综复杂经济问题，要会合理的建立模型数学。这是一切问题的前提。我们也可以考虑在确定市场需求量时建立数学模型，得出更准确的需求函数。这样不断的改进解决问题的方法，使我们的经济管理更加科学合理。

［1］Orit Gadiesh Janes. Afrenshlookatstrategy［M］. Harvard Business Rview May-June1998，P139-147.

［2］Orit Gadiesh.How to Pyourind Listry’s Profit Pools［M］，May-June1998，P149-157.

［3］赵树源.经济应用数学基础［M］.北京：中国人民大学出版社，1988.

［4］赵亚明.多元函数极值的一种新方法［M］.2003.

［5］韩伯棠.管理运筹学［M］.北京：高等教育出版社，2000.

［6］龚德恩.经济数学基础［M］.成都：.四川人民出版社，1998.

［7］程国，刘亚亚.求多元函数极值的二次型方法［J］.河西学院学报.

［8］盛祥耀.高等数学［M］.北京：高等教育出版社，2005.

［9］沙萍.高等数学［M］.沈阳：东北大学出版社，2004.

［10］洪毅.经济数学模型［M］.广州：华南理工大学出版社，1998.

［11］程理民.运筹学模型与方法教程［M］.北京：清华大学出版社，1999.

［12］毕建芝.商品出售中最优价格的确定［J］.经济论坛，2004.