不可约Z-矩阵最小特征值的改进算法
2011-01-02姜立新
姜立新
(德州职业技术学院 山东 德州 253000)
1 引言
Z-矩阵是一类比较重要的矩阵,在计算数学、图论和线性规划等学科有着广泛的应用,求其最小特征值及特征向量的算法,已有一些结果[1]-[5],本文对文献[5]中的算法做了一些改进,改进后的迭代算法过程简单,收敛速度更快并用数值实验加以验证.
定义1 设A=(aij)n×n是实矩阵,若满足非主对角元素aij≤0,则称A是Z-矩阵.
定义2 设A是n阶矩阵(n≥2),如果存在n阶排列矩阵P,使PTAP有如下形状,

其中A11和A22分别为r阶和n-r阶方阵(0≤r<n),则称A为可约矩阵,如果不存在这样的排列阵,则称A为不可约矩阵.如果是A=(aij)n×n是不可约Z-矩阵,那么可适当取使B=RI-A 是 不可约非负矩阵且bii≠0,i=1,2,…,n,如果计算出B的最大特征值λ,则ρ=R-λ就是A的最小特征值.
说明:全文中ri(A)表示矩阵A的第i行的行和,ci(A)表示矩阵A的第i列的列和.ρ(A)表示A的谱半径,AT表示矩阵A的转置.
2 主要结果
引理 1[1]设A= (aij)n×n是实矩阵,r是A的特征值,(x1,x2,…,xn)T和(y1,y2,…,yn)T分别是A和AT与r对应的特征向量,则有
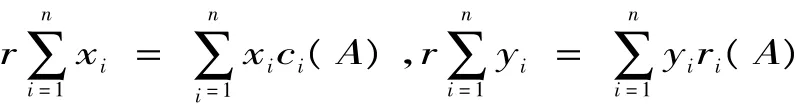
引理 2[1]设A= (aij)n×n是实矩阵,则

引理 3[1]设q1,q2,…,qn是正数,p1,p2,…,pn是任意实数,则当且仅当所有的比值相等时等号成立.

引理4[6]设A为非负不可约矩阵,则
(1)A有一正特征值等于谱半径ρ(A)
(2)A有与ρ(A)相对应的正特征向量
(3)A的任一元素增加时,ρ(A)也增加
(4)ρ(A)为A的简单特征值
定理1 设A为n阶不可约非负实矩阵且aii≠0,i=1,2,…,n,λ0是A的最大特征值,则对任意正整数k,m,有

证明 因为A非负不可约,由引理4,AT的最大特征值λ0>0且有与之对应的正特征向量 x =(x1,x2,…xn)T,不妨设则对任意正整数 k ,m,有(Ak+m)Tx = λ0k+mx,(Ak)Tx = λ0kx,由引理1可得

由于 aii≠0,i=1,2,…,n,所以对任意的正整数 k,m,有 ri(Ak) > 0,由引理3 可得,

记 A1=(aij)n×n,构造如下迭代矩阵序列
其中

定理2 设A为n阶不可约非负实矩阵且aii≠0,i=1,2,…,n,λ0是A的最大特征值,令其中 k =1,2,….
证明 对任意正整数m,由引理2,有

3 算法与数值实验
算法:
步骤1:输入不可约Z- 矩阵A=(aij)n×n,ε >0;
例 设为不可约Z-矩阵,求A的最小特征值

表1 例的计算结果(m=2时)
[1]殷剑宏.非负矩阵最大特征值的新界值[J].数值计算与计算机应用,2002,23(4):292-295.
[2]章伟,黄廷祝.不可约M-矩阵最小特征值的估计[J].工程数学学报,2004,21(8):31-34.
[3]段复建,张可村.Z-矩阵最小特征值及特征向量的数值算法[J].工程数学学报,2007,24(3):563-566.
[4]胥兰,黄廷祝.非负矩阵Perron根的上界序列[J].高等学校计算数学学报,2007,29(4):297-302.
[5]刘利斌,刘焕文,殷丽霞.不可约Z-矩阵最小特征值的数值算法[J].工程数学学报,2010,27(1):105-110.
[6]胡家赣.线性代数方程组的迭代解法[M].北京:科学出版社,1991.
[7]孙继广.矩阵扰动分析[M].北京:科学出版社,1987,1 -377.
