循环矩阵和反循环矩阵的证明及运算在Mizar系统下的实现
2011-01-02刘玲玲姜西春
刘玲玲,姜西春
(1.青岛科技大学 数理学院,山东 青岛 266061;2.青岛科技大学 数理学院,山东 青岛 266061)
0 引言
当前,数学问题的计算机证明的研究己经成为世界各国家积极研究的前沿领域.随着计算机技术的发展,人们已根据机械化方法创建了各种机器语言来编写程序,在计算机上给出相应数学问题的机器证明.目前,应用最广泛的是M izar语言系统.本文将详细介绍M izar系统下循环矩阵和反循环矩阵及其性质的实现.
本文中的所有定义及定理都收录在M izar数据库中.为了避免篇幅过长,文中举例证明了几个定义、定理,其余的证明过程省略,所有过程可在M izar数据库中查询.
1 循环矩阵的定义及性质在Mizar系统下的实现
定义1[1]数域K上的矩阵M是循环矩阵,如果M的每行均由第一行(a1,a2,...an)按同一方向依序循环得到.有时也将循环矩阵写成M=(aij)=(aj-i+1),下标m od n.以行循环矩阵为例,其定义的具体实现过程如下:
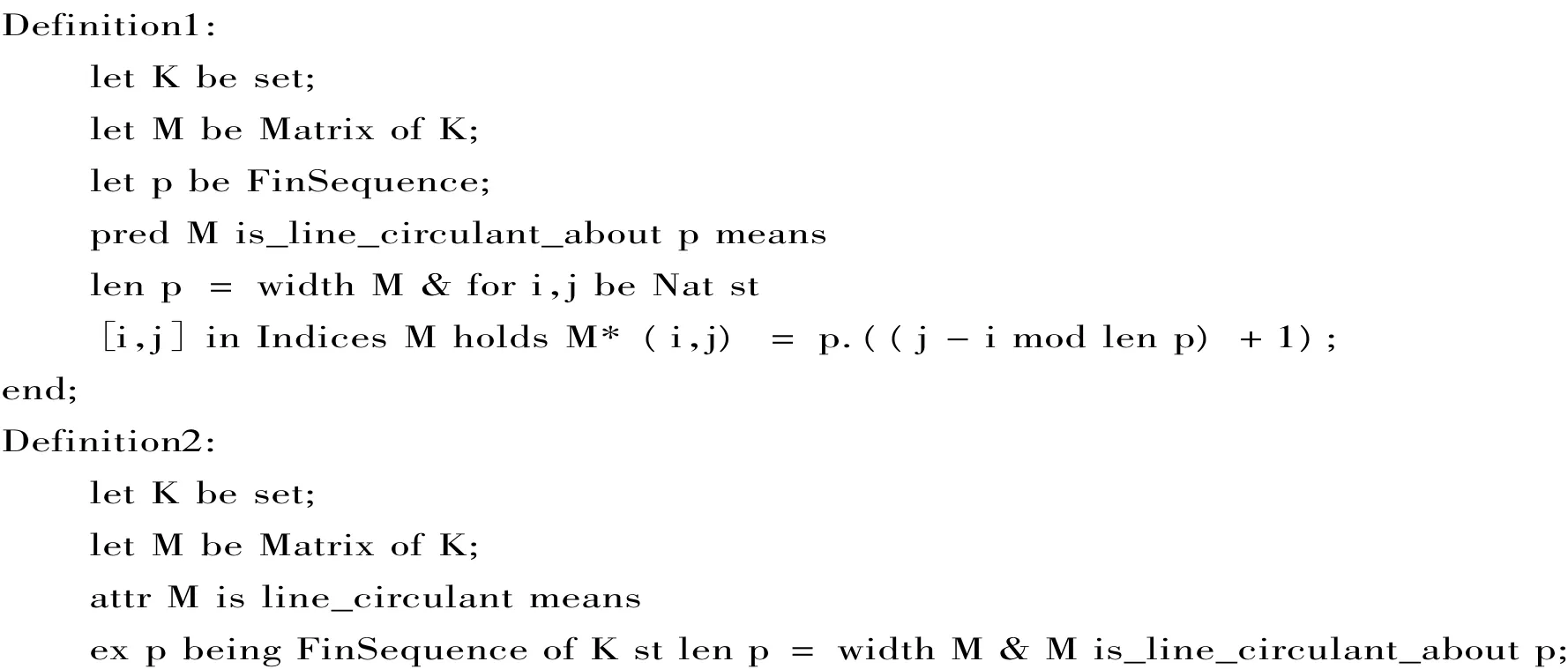
end;
为了方便在以后证明中引用,引入循环首行的定义,如下:

一个循环首行可以确定一个行循环矩阵,其M izar实现过程如下:

列循环矩阵及相关定义在M izar系统下的实现与行循环矩阵类似,此处略[2].下面是循环矩阵的性质在M izar系统下的实现:
定理1 n阶方阵A是行循环矩阵,则AT是列循环矩阵.

定理2 n阶方阵A是行循环矩阵,1≤i,j< n,且k=i+1,l=j+1,则有:Akl=Aij.

定理3 n阶方阵M1,M2是行循环矩阵,则M1+M2也是行循环矩阵.Theorem3:
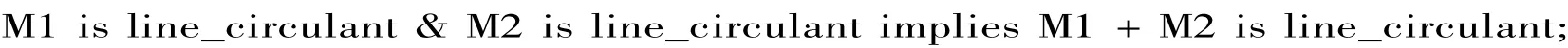
定理4 n阶方阵M1是行循环矩阵,则aM1也是行循环矩阵.

定理 5 p,q,p+q 分别是循环矩阵 M1,M2,M3的循环首行,则有:M3=M1+M2

定理6 p,ap分别是矩阵M1,M2的循环首行,则有:M2=aM1

2 反循环矩阵的定义及性质在Mizar系统下的实现
同循环矩阵的实现类似,M izar系统下的关于p的反循环矩阵与我们通常见到的反循环矩阵的定义对比如下:
定义5[1]若把一个n阶循环矩阵M的主对角线以下的元素改变符号,则得到的新矩阵称为n阶反循环矩阵.

反循环首行的实现过程与循环矩阵中的循环首行类似,这里省略,详细过程可参见M izar 数据库[2].
下面是两个关于反循环矩阵的定理在M izar系统下的实现:
定理7 M是数域K上的n阶反循环矩阵,则M对角线上的元素都为零.


定理8 M是数域K上的n阶反循环矩阵,1≤i,j<n,且k=i+1,l=j+1,
则有:Mkl=Mij

[1]北京大学数学系.高等代数[M].北京:高等教育出版社,2002.
[2]Xiaopeng Yue,Xiquan Liang.Basic Properties of Circulant Matrices and Anti- Circular Matrices[J].Formalized Mathematics 2008,16(4):355 -360.
