中国真实利率的平稳性和区制性：基于马尔科夫区制转换模型

陈国进，颜 诚

（厦门大学 王亚南经济研究院，福建 厦门 361005）

中国真实利率的平稳性和区制性：基于马尔科夫区制转换模型

陈国进，颜 诚

（厦门大学 王亚南经济研究院，福建 厦门 361005）

通过引入三种均值方差都可能不同的区制，并基于改进的马尔科夫区制转换模型对1989年2月至2010年4月中国真实利率演变的考察，结果表明不同阶段的真实利率的确存在不同的均值和方差；考虑到区制转换特征之后，真实利率大体平稳，有均值回复趋势。而以往的应用中，忽略了这种区制转换特征可能导致对真实利率预测值的系统性偏差。

真实利率；马尔科夫过程；区制转换

一、引言

真实利率（Real Interest Rate）是资金价格，是借贷成本，是新古典框架下资本的边际生产率；它既是资本市场上的关键变量，也是实体经济中一个至关重要的变量。泰勒发现，在各种影响物价水平和经济增长率的因素中，真实利率是惟一能够与物价和经济增长保持长期稳定相关关系的变量。有鉴于此，他提出了“泰勒规则”并成为自格林斯潘以来美联储政策制定的理论基础。而这一理论的前提之一是真实利率的平稳性，并且没有区制转换。这也是核心金融理论的隐含前提，不幸的是，这一前提历来遭到挑战。

在名义利率管制的中国，真实利率情况又如何呢？真实利率是平稳的吗？有没有经历区制转换呢？在哪一层次，就业率和物价均保持在由其自然法则决定的合理水平上呢？这也是中国利率市场化进程中必须面对的重要问题。由此看来，本文将国际先进理论运用于中国的数据，既为现有的理论提供了新的实证支持，具有理论意义；同时有助于研究者、投资者和管理层更深入地了解中国金融市场，具有重大现实意义。

二、文献综述

众所周知，经济学家对于真实利率波动的来源从未达成共识：有的认为来自于货币政策，有的认为来自于财政政策，至今争论不休。而更为根本的是，真实利率自身的平稳与否，长期以来也一直是财政政策、货币政策等理论研究中的一项重要议题。无论肯定还是否定，都对财政政策和货币政策的决定有着重要的政策含义。如果答案是肯定的，则真实利率受冲击的影响都是暂时的，其自身就存在着均值回复趋势；如果答案是否定的，即包含随机游走项，那么不仅会影响政策制定者的决定，而且会对一些核心的金融理论的有效力提出质疑。例如，真实利率的不平稳性不仅与Black-Scholes期权定价（B-S公式）里事前真实利率平稳的假设相违背，而且会直接导致对CCAPM理论（基于消费的资本资产定价模型，Rose，1988）[1]的拒绝。Ahn和Thompson（1988）研究表明，在其他金融理论模型中，真实利率的平稳与否也是非常重要的。特别地，如果基本的状态变量是跳跃扩散过程，甚至会使得标准的CAPM（资本资产定价模型）也要大受影响。[2]

然而，理论上已经证明了不平稳真实利率的存在。例如，West（1988）发现在一个世代交叠的工资合同模型中，旨在平滑利率的货币政策会导致不平稳的真实利率；而Delong和Summers（1986）在对总需求的不平稳冲击中，也发现了相似的结果。[3-4]

实证中，这种非平稳性在传统上通常被假设为一种随机游走的形式。虽然Fama（1975）在对美国国库券市场效率的研究中，提供了美国事前真实利率平稳的证据，但是，这是由于Fama选择了1953-1971年这一特定的样本期才导致的（Shiller，1980）。[5-6]Mishkin（1981） 通过将样本期修改为1953-1979年和1931-1952年，强有力地拒绝了真实利率平稳的假设，并由此将Fama的结论归因于自变量变异不足。[7]事实上，之前的绝大多数研究，包括不同国家和不同样本时期，都普遍拒绝了真实利率平稳的结论（如Rose，1988；Walsh，1987；Nelson和Schwert，1977；Garbade和Wachtel，1978；Fama 和 Gibbons，1982）。[1][8-11]

尽管Gokey（1990） 批评了Rose（1988）的推断程序有误，但Gokey通过修正的方法，并没有得出真实利率平稳的结论，而是发现名义利率和通货膨胀率都服从一阶单整过程，因而并没有解决问题。[12]问题的关键还在于二者是否协整，只有协整才能说明真实利率平稳；而之后的许多研究表明，这样的协整并不存在。换句话说，既然通过标准的检验方法无法拒绝单位根过程，而协整又不存在，那么真实利率就被认为是单整的、不平稳的。

然而，Garcia和Perron（1996）开创性的经验研究得出了截然不同的结论。由于他们采用了马尔科夫区制转换模型，拟合效果相对以往线性回归模型要好得多。研究结果表明，美国真实利率的均值和方差会因为外生冲击而导致区制转移；而考虑到区制转换特征之后，真实利率大体平稳，且有均值回复趋势。他们还采用1961-1986年的季度和月度两组不同来源的数据，证明美国真实利率的均值会受外部冲击的影响而出现偶尔跳跃；但在相邻两个冲击之间的时间段内，均值是恒定的。因此，他们认为在合理长度的时间段内，经验证据支持事前真实利率平稳的结论。[13]

Mills和Wang（2003）将这一研究对象由美国拓展为在同一采样周期内的欧洲四个最主要经济体（英国、法国、意大利和德国），样本期包括20世纪90年代这一普遍稳定、低通货膨胀和名义利率的时期。研究结果表明，除了少数几个区制转换外，真实利率的均值基本保持平稳。与美国类似，英国和意大利在20世纪70年代中期经历了区制转换，即前几年事前真实利率并不稳定，之后又重新步入了稳定期。相似的结论出现在法国，尽管区制转换的时间点有所推迟，经历的时间段也有所缩短。德国的表现明显不同，即20世纪最后40年里的事前真实利率一直在一个极窄的正值区间内变动，无论是石油危机还是两德统一都未对其造成实质性影响。因此，他们得出结论，如美国一样，考虑到由于外部冲击而引发的区制转移，欧洲的真实利率一般来说也是平稳的。[14]

真实利率是否平稳是一个普遍性的问题，而以上研究只针对发达国家，它是否具有普遍性呢？即在发展中国家和新兴市场能否取得一致的结论呢？针对这一问题，以中国为样本无疑具有代表性和典型性，本文的理论意义就在于此。而实践意义则在于：一方面为中国金融环境是否符合B-S公式、CCAPM等资本资产定价理论的适用性前提提供证据；另一方面为中国的货币政策当局提供借鉴。显然，真实利率的均值过高、过低或者波动性过大，都会对经济发展造成不利影响。因此，为中国的真实利率水平寻找一个均值合理、波动性适度的区制，并使之较长时间地处于该区制内，尽量防止区制转移，理应成为中国货币当局考虑的问题。

关于中国真实利率的研究主要有两类：一类是只研究通货膨胀率的变化或者名义利率及利率期限结构的变化；另一类是研究真实利率和真实汇率、经济增长、股市走向等经济变量的关系。①如赵留彦和王一鸣（2005）用两区制四阶滞后模型，考察了中国自1985年以来的通胀水平及其不确定性；吴吉林和陶旺升（2009）运用Smith的MSSV估计方法，对中国银行间7天同业拆借名义利率进行了实证分析；郑挺国（2009）对名义利率波动建模进行了详细综述，提出了一种针对MSSV模型的近似估计方法，并利用该方法对中国银行间短期拆借名义利率进行了实证研究。[15-17]但据笔者所知，很少有人对中国真实利率本身的平稳性展开研究，更少有人对中国真实利率波动的区制转换特征进行探讨和分析。刘金全和郑挺国（2006）发现，中国银行间拆借的名义利率确实发生了显著的结构性变化。[18]因此，将这种结构性变化考虑到真实利率变动模式中就显得十分必要。

本文使用1989-2010年间中国名义月度利率和CPI变化率来检验中国真实利率的时序特征。由于不同时段的序列行为特征呈现出明显差别，为了准确地描绘该时序特征，本文引入了一个改进的马尔科夫区制转换模型(Markov-Regime-Switching Model，简称MS模型)来刻画真实利率的变化过程。②

三、模型与计量方法

（一）真实利率模型

根据传统的经济理论可知，事后的真实利率等于名义利率减去通货膨胀率。即：

其中，rt代表t时刻所观察到的名义利率；πt代表从价格指数计算出的事后的通货膨胀率，即：πt=log(Pt+1/Pt)。本文中，价格指数Pt为t时刻的月度CPI数据。

根据费雪方程，事前的真实利率定义为名义利率减去预期通货膨胀率，即：

（二）马尔科夫区制转换模型

为了描述真实利率，本文假设事后真实利率yt服从一个带有均值区制转换和方差区制转换的p阶自回归过程：

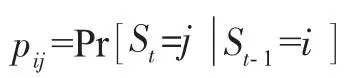
均值和方差服从：

其中，当且仅当St=i时，Sit=1；其他情况下，Sit=0。

这样，方程（1）就可以写成：

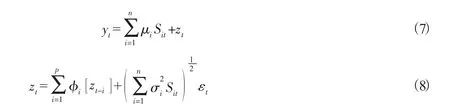
如果区制变量序列{St}的值从0到T都已知，则用对数极大似然法可得出序列{yt}的条件概率密度函数的联合分布：

（三） Hamilton滤波法

由于区制变量不可观测，仅能通过可观测序列{yt}的历史值中推断出来。使用Hamilton（1989）提出的非线性滤波法，[22]可以估计出模型的未知参数μi、、φi和pij。作为该方法的副产品，还可以得到yt的似然函数值：

同时，可以得到在第t期和滞后p期yt所处区制的联合条件概率Pr（St,St-1,…,St-p|yt,…,y1）；通过加总联合条件概率，就可以得到所谓的滤波概率，即基于t时刻信息所推断出的yt处于某种区制的概率。

滤波概率提供了样本中每一时刻yt最有可能处于哪种区制的信息，故而可以据此确认区制转换的时点。③

四、实证结果及分析

（一）数据及单整性检验

本文使用1989年2月至2010年4月间一年期存款利率的月度数据，共21年255个月。④为了确保数据长度，本文的数据取自于CEIC中国经济数据库和锐思（RESSET）金融研究数据库，并参考了《中国统计月报》。本文选取消费价格指数(CPI)变化率作为通胀指标。为了计算本月价格相对于上月的变化率，需要定基比价格指数的月度时序数据。然而，根据官方公开的统计资料，仅能获得2001年之后的月度环比通胀率，而此前只有同比通胀率。参考赵留彦等(2005)的方法，[15]利用同比通胀率以及2001年之后的月度环比通胀率，可求得1985-2000年间的定基比价格指数以及环比通胀率。⑤月度环比通胀率可在两个数据库中直接获得。

先对名义利率、通货膨胀率和真实利率进行传统的单位根协整检验，结果见表1和表2。

表1 ADF单位根检验结果

表2 协整检验结果

由表1可知，无论是在1%还是5%的显著性水平下，中国的名义利率、通货膨胀率、真实利率都不能拒绝单位根的存在，而它们的一阶差分形式是平稳的,都是AR(1)，符合建模要求。

由表2可知，名义利率和通货膨胀率之间的协整关系并不存在，无法拒绝真实利率含有单位根的原假设。

（二）滞后阶数和区制数量的选择

首先由自相关、偏相关检验可知，真实利率的偏相关系数两阶截尾，因此可以确定基本模型为两阶自回归模型。再对AR(2)模型的参数进行估计，得到模型的残差。用Eviews做雅克贝拉检验，由图1结果可知：残差偏度大于0，呈现右偏态势；峰度远大于3，呈现尖峰态势。JB检验统计量估计值均大于1%、5%对应的临界值，因而拒绝残差序列服从正态分布的零假设。然后采用BDS法检测AR(3)模型的残差，以确定残差是否独立同分布。若出现正的BDS检验统计值，则拒绝残差为独立正态同分布的假设。大量的模拟实验研究证实，BDS检测对于识别时间序列的非线性特征是十分重要的。在1%的显著性下，该统计量拒绝原假设(残差独立同分布)，这充分说明了真实利率时间序列非线性的存在。

而线性模型可视为马尔科夫区制转换模型的一种特例。如果区制转换模型仅含有一个区制而不是在两区制之间随机转换，即退化为线性过程。理论上可以对区制数量的选择做严格的检验，但根据Garcia和Perron（1996）、Mills和Wang（2003）可知，马尔科夫区制转换模型的区制数量选择不能通过通常的似然比检验、拉格朗日乘子检验或者Wald检验来决定，因为它们的渐进分布不是标准的。参考AIC和HQ模型选择准则，利用Garcia和Perron（1996） 附录中的方法（Davies的上确界检验，Gallant的检验程序），本文采用三区制马尔科夫区制转换的两阶滞后自回归模型。为了稳健起见，本文一并列出了对季度数据回归和采用二区制两阶滞后模型回归的结果。结果显示，三区制两阶滞后模型表现最好。

（三）模型的估计结果

表3给出了用GAUSS程序运行的实证结果，所得参数大多显著。图2给出了一年期存款利率的三种区制的滤波概率图和事后真实利率图。

图1 雅克贝拉检验结果

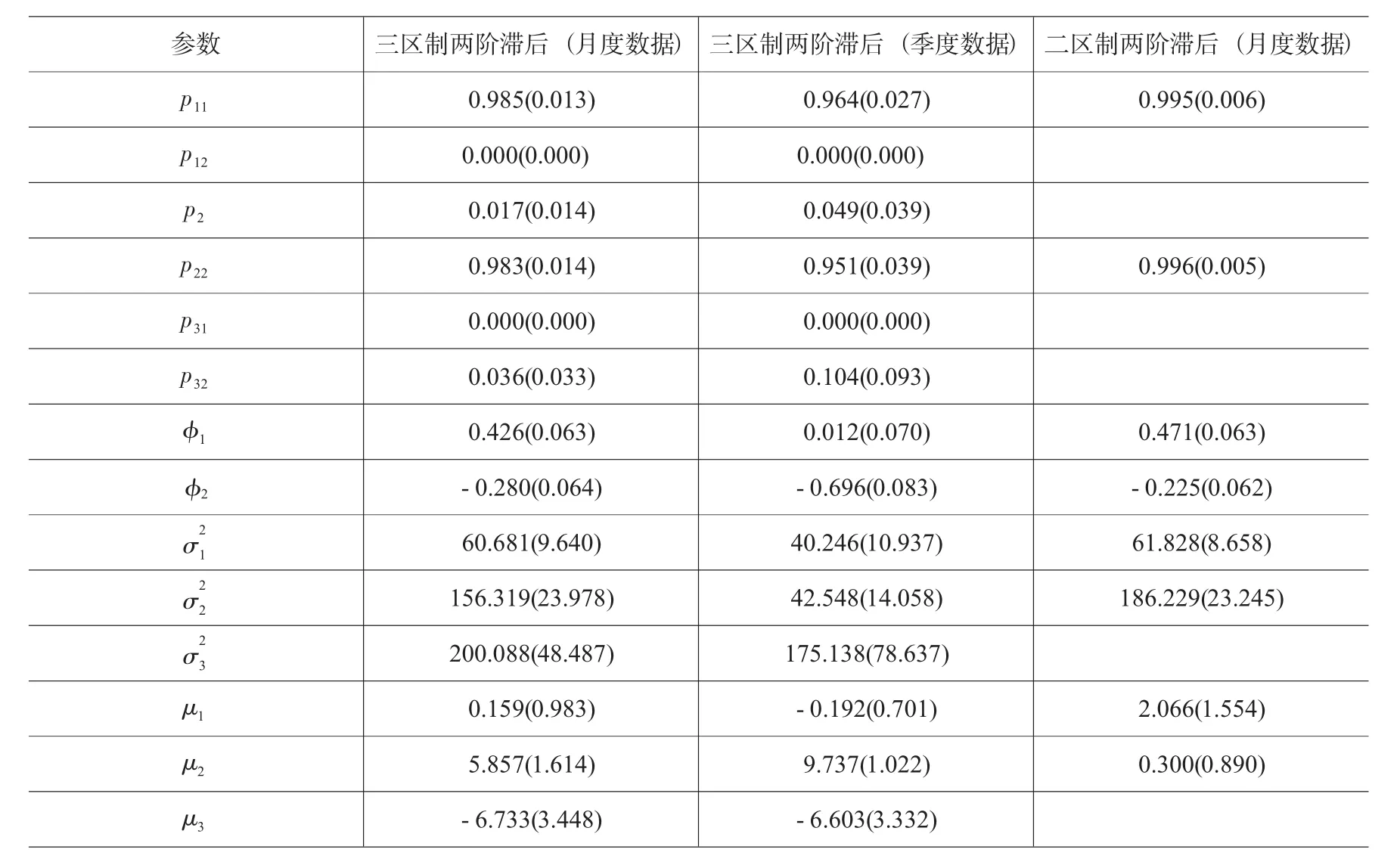
表3 模型参数估计结果

从图表中可以清楚地看出，一年期存款利率的事后真实利率在1993年中期之后，经历了一个从低利率区制到高利率区制再到中等利率区制的过程；而在长时间的中等利率区制过程中，包含着一个短暂的低利率区制。如果简单地以0.5的概率为分界点来划分，即如果只要某区制的滤波概率大于0.5就认为当月事后真实利率处于该区制中，那么从图中可以清楚地看出：从1989年5月到1993年4月（即第4个月到第48个月）、从1995年7月到2001年8月（即从第75个月到第148个月） 处于高利率区制；从1993年5月到1995年6月（即从第49个月到第74个月）、从2008年3月到2008年8月（即从第227个月到232个月） 处于低利率区制；从2001年9月到2008年2月（即从第149个月到第226个月）、从2008年9月（即从第233个月）至今处于中等利率区制。

图2 三种区域的滤波概率及事后真实利率图

改革开放以来，不同时段的通胀率呈现出不同的走势，但在1988年和1994年前后两度达到高峰，其他年份则相对平稳。由于数据的可得性，1988年不在本文的分析范围内。由于价格改革，不少消费品价格在1988年放开，导致通胀上升。为了抑制通胀，政府从1988年第四季度开始采取提高银行存款利率、减少基本建设投资、延缓生产资料价格放开时间等措施，至1988年底物价涨幅开始回落、银行储蓄存款上升，较为稳定的物价水平持续到1993年。这一阶段正好对应着本文的所得结论：1993年之前真实利率处于第二个高利率区制的阶段。

1992年邓小平同志南巡讲话推动了对外开放在全国范围内的全面展开，推动了中国经济高速扩张，也推动了CPI的快速上涨。1993年到1995年是改革开放以来的第二个高通胀阶段，其中1994年的年通胀率超过25%，为建国以来最高水平。为了刺激经济增长，货币发行量和商业银行发放的贷款总额从1992年开始迅速增长，⑥货币过度供给的后果从1993年开始显现出来；粮价改革以及能源价格的提高，也是物价上涨的直接诱导因素。而这一阶段正好对应着本文的所得结论：从1993年5月到1995年6月真实利率处于低利率区制的阶段。

1993年到1995年的价格改革和调整尽管导致了高通胀，然而这一阶段之后，价格的市场形成机制得以确立（易纲，1996）。[23]从1996年开始通胀明显降低，月度通胀率接近于零。1997年经济“软着陆”，随后中国经济再次进入紧缩期并持续到2002年。事实上，1996年12月到2003年1月，CPI累计增长-3.7%,CPI累计变化率接近于0。这一阶段同1995年前通胀水平较高且波动剧烈的特点形成了鲜明对比。尽管货币政策方面，央行为了应对1996年到1999年亚洲金融危机和促进中国货币改革(由直接调控转向间接调控)，在1997年5月到1999年6月的两年内连续六次下调人民币利率，但是，通胀率的下降作用更为明显。这一阶段正好对应着本文的所得结论：从1995年7月到2001年8月真实利率处于高利率区制的阶段。

从2001年9月至今，CPI累计增长16.8%；鉴于长达10年之久的时间，年通胀率为1%左右，进入了通胀率低水平的稳定阶段。而且，这段时间的货币政策也相对比较稳定，从1999年8月到2005年底的6年时间内，央行一共才两次调整存款准备金率，三次调整利率。而这一阶段正好对应着本文的所得结论：从2001年9月至今真实利率处于中等水平利率区制的阶段。这也为中国经济所谓的“黄金十年”提供了货币层面上的解释。

惟独2008年3月到2008年8月这个短暂的低利率区制，无法从CPI、通货膨胀率等方面得到解释。要知道，这一阶段的CPI累计增长-0.6%。但如果从货币政策方面看，道理就非常简单了。2007年到2008年我国股市达到顶峰，中国人民银行为应对资产价格泡沫、稳定通货膨胀预期，连续五次上调存款准备金率，货币政策由宽松向从紧转变。直至全球性金融危机爆发，货币政策“急刹车”，央行多次调整存款准备金率和利率。这一外生冲击正好显示在这一短暂的低利率区制中。

综上所述，从这段经济发展的历程来看，本文模型识别出来的真实利率的三区制与中国实际情况是相当吻合的。本文认为，对真实利率的滤波概率分析，不仅可以识别历史和当前利率、通货膨胀率所处的状态，进而运用于对经济发展的历史分析，而且还可以为将来经济环境预测提供更多的信息。综合各图表可知，最近几个月真实利率处于中等区制的滤波概率开始下降，处于低区制的滤波概率有所抬头。这是否预示着前两年“4万亿”的投入和“十大产业振兴政策”的货币政策效果开始显现，高通胀近在眼前呢？这是个值得深思的问题。

（四）简要讨论与相关分析

首先，由表3可知，在中等水平、高水平、低水平这三种区制中，真实利率的方差和均值各不相同。很显然，波动性依次增大，中等水平的真实利率的波动性最小。根据古典经济理论，真实利率的波动性越小，对经济增长的影响越有利。如何防止最近出现的真实利率从“最优的”中等利率区制向低利率区制转换，是货币当局急需考虑的问题。

其次，与美国不同，中国真实利率的自回归系数和φ1+φ2都远小于1，且显著不为零。这说明考虑到区制转换特征之后，中国的真实利率大体平稳，且有均值回复趋势。

再次，表3前六行给出的是各种区制之间的转换概率。Pij表示由区制i到区制j的转换概率。而P11，P22，P33都小于0.9，这说明从历史角度上看，一旦真实利率处于某种区制，就有在该区制持续一段时间的趋势。

最后，根据Kim和Nelson（1999）的研究，[24]某一区制的平均持续期D(Si)=1/（1-pij）。由表中数据P11=0.985、P22=0.983、P33=1-P31-P32=0.964，算出三种区制的持续期分别为66.7个月、58.8个月和27.8个月。这与之前识别出来的各区制持续时间基本吻合。

五、总结

本文通过引入三种均值方差都可能不同的区制，并基于改进的马尔科夫区制转换模型（Hamilton，1989）考察了1989年2月至2010年4月中国真实利率的演变。结果表明，不同阶段的真实利率的确存在不同的均值和方差。考虑到区制转换特征之后，真实利率大体平稳，有均值回复趋势。以往应用中忽略了这种区制转换特点，导致了对真实利率预测值的系统性偏差。这不仅为Fama（1975）的论点提供了进一步的支持，为经济金融领域其他更多更重要的研究奠定了现实基础，而且为中国的货币当局提供了有用的借鉴。

值得注意的是，尽管发生区制转换的时间是内生决定的，可以解释为受对应时间的经济事件的影响，但不应当将本文的结构模型理解为政策制定者可以操控真实利率的工具，在长期内尤其如此。本文的结果仅仅可以被视为是资产定价模型的一阶均衡条件的简化形式。比如在Bonomo和Garcia(1991)所提出的以及之后系列相关文献所引用的交换经济的资产定价模型中，外生给定资源禀赋条件，真实消费的变化遵循一个三区制马尔科夫区制转移过程。[25]在这样的模型中，真实利率的均衡值也遵循一个三区制转移过程。尽管对真实消费变化的冲击可能来自于名义利率的改变，也可能来自于通货膨胀率的变动，但终归都要通过真实利率来产生作用；而本文的模型正好紧紧抓住了上述特征。

最后需要指出的是，由于研究方法的性质所限，从统计角度上看，本文的模型并不应该被视为为真实利率提供了一种很好的预测方法，特别是中长期预测。虽然本文的结果显示，在本文所分析的序列长度中只出现了三种区制，每种区制只出现了一次，但是并不能排除以后还会有第四种甚至第五种区制出现的可能。本文的结果还显示，对于真实利率的这种统计性质用事后描述的方法展现出来，对于将来的研究是极富指导意义的，特别是对模型设计方面。例如：研究涉及到真实利率的时候，是否假设其包含一个均值和方差在某些时刻可能发生区制转换的噪音成分，是一个值得考虑的问题。简单地说，本文发现了区制的数量、每一区制中均值和方差的大小、区制转换的时间以及噪音成分的动态变化性质等。

注 释：

①前一类主要关注银行间同业拆借利率、国债回购利率等短期利率，优点是相对市场化；后一类往往使用存贷款利率，优点在于影响范围大、覆盖时间长，更具有便利性。本文数据与后一类一致。

②魏巍贤、陈智文和王建军（2006）利用相似的模型分析了世界油价的波动，取得了很好的效果，且相对于其它线性模型而言，该模型在对油价的预测效果方面具有明显的优势。[19]李宇嘉和陆军（2007）借鉴过同样的技术。[20]

③同理可以计算出平滑概率，即基于全样本信息推断出的处于某种状态的概率（Hamilton，1989）。[22]虽然平滑概率所使用的信息更充分，因而可能会得出更为精确的结果，但在本文中二者的结果几乎是一样的。考虑到滤波概率的预测作用，本文只报告滤波概率。

④本文对各期存贷款利率都分别做了检验，结论大体一致。限于篇幅，只报告一种。

⑤已知2001年环比数据和此前年份同比数据，可倒推2000年环比数据。2000年t月环比指数=2001年t-1月同比指数÷2001年t月同比指数×2001年t月环比指数。同样地，已知2000年环比数据和此前年份同比数据，可倒推1999年环比数据。依此类推。

⑥从1992年起，现金发行或信贷规模两项同时大幅突破预定计划。现金发行1991年超过预定计划7%；1992年超过93%；1993年超过53%。信贷规模1990年超过预定计划61%；1991年、1992和1993年分别超过38%、25%和28%。结果，1990-1993年间，M2余额增长了157.9%。

[1]Rose,A.K.Is the real interest rate stable?[J]．Journal of Finance,1988，43：1095-1112.

[2]Ahn,CM HE Thompson.Jump-Diffusion Processes and the Term Structure of Interest Rates[J].Journal of Finance 1988，(43)：155-174.

[3]West,K.D.On the interpretation of near random walk behaviour in GNP[J].American Economic Review,1988，78：202-209.

[4]DeLong,J.B.and L.H Summers.Is increased price flexibility stabilizing?[J].American Economic Review,1986，76(5)：1031-1044.

[5]Fama,E F.Short-Term Interest Rates as Predictors of Inflation[J].American Economic Review,American Economic Association，1975，65(3)：269-282.

[6]Shiller,R J.Can the Fed Control Real Interest Rates?in S.Fisher(ed),Rational Expectations and Economic Policy[M].Chicago:University of Chicago Press，1980.

[7]Mishkin,F S.The Real Interest Rate:An Empirical Investigation[C].Carnegie-Rochester Conference Series on Public Policy，1981，15：151-200.

[8]Walsh,C E.Three Questions Concerning Nominal and Real Interest Rates[J].Economic Review Federal Reserve Bank of San Francisco,1987，(4)：4,5-20.

[9]Nelson,C,and G.W Schwert.Short-term Interest Rates as Predictors of Inflation:On Testing the Hypothesis that the Real Rate of Interest Is Constant[J].American Economic Review，1977，67：478-486.

[10]Garbade,K,and P Wachtel.Time Variation in the Relationship between Inflation and Interest Rates[J].Journal of Monetary Economics，1978，(4)：755-765.

[11]Fama,E F.,and M R.Gibbons.Inflation,Real Returns,and Capital Investment[J].Journal of Monetary Economics，1982，(9)：297-323.

[12]Gokey,T.C.Stationarity of Nominal Interest Rates,Inflation,and Real Interest Rates[J].mimeo,Oxford University,1990.

[13]Garcia R and P Perron.An Analysis of the Real Interest Rate under Regime Shifts[J].The Review of Economics and Statistics,MIT Press，1996，78(1)：111-125.

[14]Mills T C,P Wang.Regime shifts?in?European real interest rates[J].Review of world economics,2003.

[15]赵留彦，王一鸣.中国通胀水平与通胀不确定性：马尔柯夫域变分析[J].经济研究，2005，(8)：60-72.

[16]吴吉林，陶旺升.基于机制转换与随机波动的我国短期利率研究[J].中国管理科学，2009，17(3)：40-46.

[17]郑挺国.基于有限混合状态空间的金融随机波动模型及应用研究[M].长春：吉林大学，2009.

[18]刘金全,郑挺国.利率期限结构的Markov区制转移模型与实证分析[J].经济研究，2006，(11)：82-91.

[19]魏巍贤，陈智文，王建军.三状态马尔可夫机制转换模型研究——在世界油价波动分析中的应用[J]．财经研究，2006第6期。

[20]李宇嘉，陆 军.风险溢价、预期损失与预测贷款损失准备金[J].当代财经，2007，(12)：50-56.

[21]赵留彦.中国通胀预期的卡尔曼滤波估计[J].经济学（季刊），2005，(7).

[22]Hamilton J D.A new approach to the economic analysis of nonstationary time series and the business cycle[J].Econometrica，1989，57(2)：357-384.

[23]易 纲.中国的货币、银行和金融市场：1984-1993[M].上海：上海三联书店和上海人民出版社，1996.

[24]Kim C J,C R Nelson.State-Space models with regime switching[M].MA：MIT Press，1999.

[25]Bonomo,M,and R Garcia.Consumption and Equilibrium Asset Pricing:An Empirical Assessment[J].CRDE Working Paper.Universite de Montreal，1991.

Stability and Regime of China’s Real Interest Rate：Based on Markov Regime Switching Model

CHEN GUO-jin,YAN Cheng
(Xiamen University,Xiamen 361005,China)

By introducing three regimes possibly with different means and variances and based on the improved Markov-regime-switching model,this paper conducts an investigation on the evolution of China’s real interest rates from February 1989 to April 2010.The results indicate that there do exist different means and variances of the real interest rate at different stages.Considering the characteristics of regimes switching,the real interest rates is generally stable,with mean-reversion tendency.While in the past applications,the ignorance of these characteristics may lead to systematic deviation of the predicted values of the real interest rates.

real interest rate;Markov process;regime switching

责任编校：魏 琳

F830.9

A

1005－0892(2010)10－0041－10

2010-06-29

教育部人文社科基金项目（09YJA790118）；教育部人文社科基金项目（08JA790109）

陈国进，厦门大学教授，博士生导师，主要从事宏观经济学和金融计量经济学研究；颜 诚，厦门大学博士研究生，主要从事宏观经济学和金融计量经济学研究。